Арифметические устройства

Цифровые электронные средства обработки информации по существу выполняют с двоичными числами арифметические операции: сложение, вычитание, умножение, деление, а также сравнение, выделение большего, определение четности и другие. Важнейшей из арифметических операций, которая лежит в основе других, является сложение, производимое сумматором.

Сумматоры – это функциональные узлы (блоки), выполняющие сложение многоразрядных чисел и построенные с помощью объединения одноразрядных сумматоров, соединенных цепями переноса.

Сумматор последовательного действия строят по простой схеме с единственным одноразрядным сумматором (рис.6.4).

Рис.6.4. Сумматор последовательного действия

При этом слагаемые хранятся в n - разрядных регистрах, которые синхронно осуществляют их сдвиг. Получившееся значение суммы для соответствующего разряда заносится в выходной регистр результата, а значение переноса задерживается на один такт и подается на вход (наличие регистров для хранения слагаемых и суммы необходимо во всех типах сумматоров). Основным недостатком последовательного способа организации суммирования многоразрядных чисел является большое время выполнения операции.

Параллельный сумматор содержит n одноразрядных сумматоров (рис.6.5), на входы которых разряды слагаемых подаются одновременно (в одном такте работы).

A₁ B₁

A₃ B₃

A_k B_k

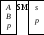
Рис.6.5. Сумматор параллельного действия

Разновидности параллельных сумматоров отличаются способами организации переноса. Последовательный перенос означает, что выход переноса р_вых младшего разряда непосредственно подключают к входу р_вх следующего за ним старшего разряда. В этом случае все разряды двоичного числа складываются одновременно, а сигнал переноса проходит сумматоры последовательно по мере его появления.

Быстродействие сумматора ограничено задержкой переноса, т.к. формирование сигнала переноса на выходе старшего разряда не может производиться до тех пор, пока сигнал переноса младшего разряда не распространится по всей цепочке. Максимальное время сложения (распространения сигнала) будет t_s = n t₁ , где t₁ – время задержки сигнала в одноразрядном сумматоре.

Ускорение процесса сложения достигается за счет аппаратного усложнения устройства, т.е. применения блока ускоренного переноса (комбинационной схемы), который обеспечивает одновременный перенос во всех разрядах двоичного числа. В каждом разряде дополнительно формируют два управляющих сигнала и работа схемы ускоренного переноса происходит в соответствии с формулой

.

Для сложения чисел большой разрядности применяют соединение сумматоров меньшей разрядности (рис.6.6).

Рис. 6.6. Наращивание разрядности сумматора

Указанное соединение называется наращиванием разрядности. При этом младшие разряды чисел складываются в сумматоре SM₁, а старшие и перенос - в сумматоре SM₂. В результате получается сумматор с удвоенной разрядностью.

Операция вычитания в цифровой технике заменяется сложением уменьшаемого с вычитаемым, представленным в дополнительном коде. Для построения вычитателя используют сумматор с входными инверторами (рис.6.7), преобразующими операнд В в обратный код, а добавление по входу переноса единицы переводит его в дополнительный код, который суммируется с прямым кодом операнда А.

Рис.6.7. Вычитатель на основе сумматора

Узел, совмещающий операции сложения и вычитания, получают заменой инверторов элементами “исключающее ИЛИ”, которые в зависимости от управляющего сигнала на одном из входов работают как повторители или инверторы.

Производительность вычислительного устройства обработки информации существенно зависит от времени выполнения действия умножения, которое включает множество операций сложения и сдвига. Наиболее быстродействующими аппаратными умножителями являются узлы, базирующиеся на схемах комбинационной логики. Операция умножения двухразрядных чисел и , записанная в форме , содержит перемножение разрядов чисел, реализуемую элементом И и суммирование. Завершенный функциональный узел одновременно выполняет умножение операндов и суммирование произведения с числами K и M, т. е. реализует формулу , позволяющую наращивать разрядность. Блок состоит из четырех одинаковых ячеек (рис.6.8), связанных между собой.

Рис.7.8. Структура множительной ячейки

Преобразование логики выполнения операций позволило разработать схемы быстрых умножителей.

На основе узлов полусумматоров или ЛЭ “исключающее ИЛИ” реализуют устройства сравнения многоразрядных двоичных чисел, называемые цифровыми компараторами. Логическую схему “исключающее ИЛИ” используют в качестве одноразрядного компаратора. Сравнение производится во всех разрядах одновременно и результат отображается уровнем на выходе.

При сравнении чисел и элемент “исключающее ИЛИ” выполняет операции с каждым двоичным разрядом в соответствии с алгоритмом , где и . При сравнении разрядов на основном и дополнительных выходах элемента имеем уровни сигналов: s_i = 0 при a_i = b_i , с_i = 1 при a_i > b_i , d_i = 1 при a_i < b_i . Если выходы s_i всех разрядов подключить к входам элемента ИЛИ – НЕ, то единичный уровень сигнала на его выходе будет только при нулевых значениях на всех входах s_i = 0, т.е. при равенстве чисел.

Объединение двух элементов с помощью логической схемы, обеспечивающей выполнение условий s_1,0 = 0 при A = B, а также с₁ = 1 или s₁ = 0 и с₀ = 1 при A > B, приводит к блоку двухразрядного компаратора, способного определять и регистрировать при равенстве A = B и характер неравенств (φ = 1) при A < B или (f = 1) при A > B (рис.6.9,а).

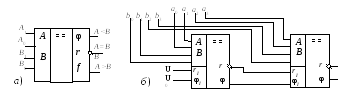
Рис.6.9. Двухразрядный компаратор (а) и каскадное объединение (б)

Для наращивания разрядности сравниваемых чисел применяют каскадное или пирамидальное соединение нескольких компараторов. Сравнение производят, начиная с младших разрядов чисел, которые подают на входы первого компаратора (рис.7.9,б).

В виде отдельных ИМС средней степени интеграции производят целый ряд арифметических устройств, вырабатывающих управляющие сигналы при определенных соотношениях в кодах чисел (четности чисел, равнозначности кодов).