HaoZip RAR Архив_1 / ЛЕКЦИЯ 14

ЛЕКЦИЯ 14

Тригонометрический ряд — числовой ряд вида:

^[1].

Тригонометрический ряд называется рядом Фурье функции , если коэффициенты  и  определяются следующим образом:

где  — это интегрируемая функция^[1].

Не каждый тригонометрический ряд является рядом Фурье.

Типичная задача в теории тригонометрических рядов: найти, при каких значениях переменной  данный тригонометрический ряд сходится.

ТРИГОНОМЕТРИЧЕСКАЯ СИСТЕМА

одна из важнейших ортогональных систем функций. Функции Т. с. 1, cosx, sinx, . ..,cosnx,sinnx, . .. ортогональны на любом отрезке вида  а функции

ортонормированы на этом отрезке. Т. с. полна и замкнута в пространстве  при  а также в пространстве  непрерывных  -периодических функций. Эта система образует базис в пространстве  при  Ряды по Т. с. изучаются в теории тригонометрических рядов.  Наряду с Т. с. широкое применение находит комплексная тригономстрич. система  Функции этих систем связаны друг с другом формулами Эйлера.

  Ряд Фурье       Тригонометрическая система 

     Коэффициенты Фурье функции f периода  

либо

     Ряд Фурье функции f 

     Если f четная, то  ряд Фурье 

     Если f нечетная, то 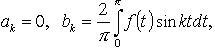 ряд Фурье 

     Если функция f кусочно-дифференцируема, то

Условие разложимости функции в ряд Фурье

О п р е д е л е н и е. Функциональный ряд

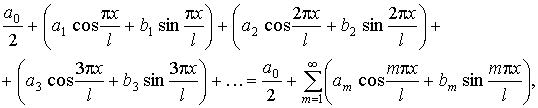 (54)

членами которого являются синусы и косинусы от кратных значений аргумента, называется тригонометрическим рядом.

Здесь l > 0 – произвольное число; a₀, a_m, b_m (m=1, 2, 3) – постоянные коэффициенты ряда. Так как все члены тригонометрического ряда синусы и косинусы углов, кратных , то их сумма S(x), если она существует, является периодической функцией от х с периодом 2l: S(x) = S(x + 2l). Естественно, возникает задача: нельзя ли представить всякую периодическую функцию в виде тригонометрического ряда.

О п р е д е л е н и е. Рядом Фурье для функции f(x) в интервале [–l, l] называется тригонометрический ряд вида (54) с коэффициентами ряда a_m, b_m, вычисленными по формулам Фурье:

, m = 0, 1, 2, … ; (55)

, m = 1, 2, 3, …. (56)

Достаточные условия разложимости функции в ряд Фурье сформулированы в теореме Дирихле.

Т е о р е м а. Если в интервале [–l, l] функция f (x) имеет конечное число точек разрыва первого рода (или непрерывна) и конечное число точек экстремума (или не имеет их вовсе), то ее ряд Фурье сходится, т.е. имеет сумму S (x) во всех точках указанного интервала.

При этом:

а) в точках непрерывности функции f (x) ряд сходится к самой функции: S (x) = f (x);

b) в каждой точке разрыва x_k функции f(x) ряд сходится к полусумме односторонних пределов функции слева и справа:

;

c) в обеих граничных точках интервала [–l, l] ряд сходится к полусумме односторонних пределов функции при стремлении х к этим точкам изнутри интервала:

.

Часто периодическая функция f (z) задается на интервале [– ,  ]. В этом случае ряд Фурье для f (z) записывается в несколько ином виде:

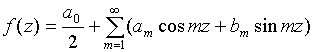, (57)

где

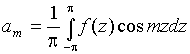 (m = 0, 1, 2, …); (58)

 (m = 1, 2, 3 …). (59)

К этому ряду также применима теорема Дирихле и полученные ниже выводы.

Признак Дирихле сходимости несобственных интегралов первого рода[править | править исходный текст]

Пусть выполнены условия:  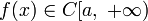и имеет на  ограниченную первообразную , то есть ; функция ; . Тогда  сходится.

• Очевидно, что вместо второго условия можно также записать .

• Условие монотонности в признаке Дирихле существенно.

Однако, условие монотонности не является необходимым.

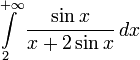 — сходится.

• Условие ограниченности первообразной в признаке Дирихле также является существенным, но не является необходимым.

• усть f(x) - четная функция с периодом 2L, удовлетворяющая условию f(-x) = f(x) .

• Тогда для коэффициентов ее ряда Фурье находим формулы:

• =

• =

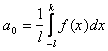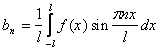• = 0, где n=1,2, ...

• Таким образом, в ряде Фурье для четной функции отсутствуют члены с синусами, и ряд Фурье для четной функции с периодом 2L выглядит так:

• 

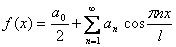
• Пусть теперь f(x) - нечетная функция с периодом 2L, удовлетворяющая условию f(-x) = - f(x).

• Тогда для коэффициентов ее ряда Фурье находим формулы:

• , где n=1,2, ...

• Таким образом, в ряде Фурье для нечетной функции отсутствует свободный член и члены с косинусами, и ряд Фурье для нечетной функции с периодом 2L выглядит так:

• 

• Если функция f(x) разлагается в тригонометрический ряд Фурье на промежутке то 

• , где ,

• ,

• ,

• Если f(x) разлагается в тригонометрический ряд Фурье на [0,L], то доопределив заданную функцию f(x) соответствующим образом на [-L,0]; далее периодически продолжив на (T=2L), получим новую функцию, которую разлагаем в тригонометрический ряд Фурье.

• Для разложения в ряд Фурье непериодической функции, заданной на конечном произвольном промежутке [a,b], надо : доопределить на [b,a+2L] и периодически продолжить, либо доопределить на [b-2L,a] и периодически продолжить.

• Ряд Фурье для произвольного интервала.

• Разложение периодической функции с периодом L.

• Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.

• Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид

• 

• Где коэффициенты ряда Фурье, 

• 

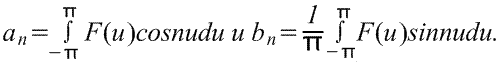
• Однако чаще приведенную выше формулу приводят к зависимости от х. Поскольку u=2πх/L, значит, du=(2π/L)dx, а пределы интегрирования - от -L/2 до L/2 вместо - π до π. Следовательно, ряд Фурье для зависимости от х имеет вид

• 

• где в диапазоне от -L/2 до L/2 коэффициенты ряда Фурье,

• 

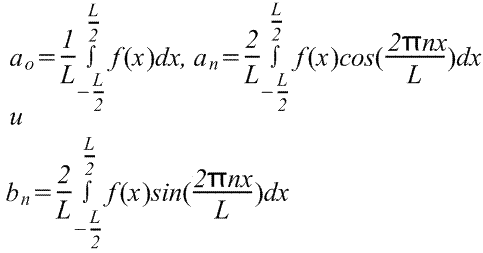
• (Пределы интегрирования могут быть заменены на любой интервал длиной L, например, от 0 до L)