
HaoZip RAR Архив_1 / ЛЕКЦИЯ 11
.docЛЕКЦИЯ 11
Функциональный
ряд —
ряд, каждым членом которого, в отличие
от числового
ряда,
является не число, а функция ![]() .
.
![]()
![]() —
n-ная
частичная сумма.
—
n-ная
частичная сумма.
Сходимость[править | править исходный текст]
Ряд
называется сходящимся поточечно, если
последовательность ![]() его
частичных сумм сходится поточечно.
его
частичных сумм сходится поточечно.
Ряд
называется сходящимся равномерно, если
последовательность ![]() его
частичных сумм сходится равномерно.
его
частичных сумм сходится равномерно.
Необходимое условие равномерной сходимости[править | править исходный текст]
![]()
Критерий Коши равномерной сходимости[править | править исходный текст]
Критерий
Коши для последовательности ![]() .
Чтобы последовательность функций
.
Чтобы последовательность функций ![]() ,
определённых на множестве
,
определённых на множестве ![]() ,
равномерно сходилась на этом множестве,
необходимо и достаточно, чтобы для
всякого
,
равномерно сходилась на этом множестве,
необходимо и достаточно, чтобы для
всякого ![]() существовал
номер
существовал
номер ![]() ,
такой, что при всех
,
такой, что при всех ![]() больше
либо равных
больше
либо равных ![]() ,
одновременно для всех
,
одновременно для всех ![]() выполнялось
неравенство
выполнялось
неравенство ![]()
Абсолютная и условная сходимость[править | править исходный текст]
Ряд ![]() называется
абсолютно сходящимся, если
называется
абсолютно сходящимся, если ![]() сходится.
Абсолютно сходящийся ряд сходится.
сходится.
Абсолютно сходящийся ряд сходится.
Если
ряд ![]() сходится,
а
сходится,
а ![]() расходится,
то ряд
расходится,
то ряд ![]() называется
сходящимся условно. Для таких рядов
верна теорема
Римана о перестановке членов условно
сходящегося ряда.
называется
сходящимся условно. Для таких рядов
верна теорема
Римана о перестановке членов условно
сходящегося ряда.
Равномерная
сходимость последовательности функций (отображений)
— свойство последовательности ![]() ,
где
,
где ![]() —
произвольное множество,
—
произвольное множество, ![]() — метрическое
пространство,
— метрическое
пространство, ![]() сходиться
к функции (отображению)
сходиться
к функции (отображению) ![]() ,
означающее, что для любого
,
означающее, что для любого ![]() существует
такой номер
существует
такой номер ![]() ,
что для всех номеров
,
что для всех номеров ![]() и
всех точек
и
всех точек ![]() выполняется
неравенство
выполняется
неравенство
![]()
Обычно
обозначается ![]() .
.
Это условие равносильно тому, что
![]()
Признак Вейерштрасса
Рассмотрим
ряд: ![]()
Пусть
существует последовательность ![]() такая,
что для любого
такая,
что для любого ![]() выполняется
неравенство
выполняется
неравенство ![]() ,
кроме того, ряд
,
кроме того, ряд ![]() сходится.
Тогда ряд
сходится.
Тогда ряд ![]() сходится
на множестве
сходится
на множестве ![]() абсолютно
и равномерно.
абсолютно
и равномерно.
Для доказательства достаточно проверить справедливость критерия Коши.
Теорема. (почленное
интегрирование ряда). Пусть ряд ![]() равномерно
сходится к своей сумме
равномерно
сходится к своей сумме ![]() на
отрезке
на
отрезке ![]() и
все
и
все ![]() .
Тогда
.
Тогда ![]()
![]() .
.
Доказательство. Обозначим
при произвольном ![]() ,
, ![]() .
Тогда
.
Тогда ![]() -
непрерывная функция и, т.к. по предыдущей
теореме
-
непрерывная функция и, т.к. по предыдущей
теореме ![]() -
непрерывная функция,
-
непрерывная функция, ![]() -
также непрерывная функция. Тогда
-
также непрерывная функция. Тогда ![]()
![]() .
Для доказательства теоремы достаточно
доказать, что
.
Для доказательства теоремы достаточно
доказать, что ![]() при
при ![]() ,
т.к., по определению,
,
т.к., по определению, ![]()
![]() .
Но
.
Но ![]() . Поэтому
при
. Поэтому
при ![]()
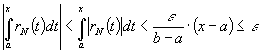 и
требуемое утверждение доказано.
и
требуемое утверждение доказано.
Замечание. Для
функциональных последовательностей
эта теорема формулируется следующим
образом: Пусть ![]() на
на ![]() .
Пусть
.
Пусть ![]() .
Тогда
.
Тогда ![]() .
.
Теорема. (о почленном дифференцировании ряда).
Пусть:
-
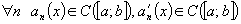 ;
; -
Ряд
 сходится
на
сходится
на  (и
пусть его сумма обозначена
(и
пусть его сумма обозначена 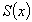 );
); -
Ряд
 равномерно
сходится на
равномерно
сходится на 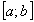
.
Тогда ![]() или,
иными словами,
или,
иными словами,  .
.
Доказательство. Обозначим ![]() -
сумму ряда
-
сумму ряда ![]() .
Тогда
.
Тогда ![]() -
непрерывная на
-
непрерывная на ![]() функция.
Поэтому
функция.
Поэтому ![]() существует
ее интеграл от
существует
ее интеграл от ![]() и
он, по предыдущей теореме, равен
и
он, по предыдущей теореме, равен ![]()
![]() .
Значит,
.
Значит, ![]() или
или  .
.
Замечание. Соответствующая
теорема для последовательностей может
быть сформулирована так: Пусть ![]() .
Пусть
.
Пусть ![]() ,
, ![]() и
пусть
и
пусть ![]() ,
, ![]() .
Тогда
.
Тогда ![]() ,
или
,
или ![]() .
.
Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:
![]()
в
котором коэффициенты ![]() берутся
из некоторого кольца
берутся
из некоторого кольца ![]() .
.
-
Первая теорема Абеля: Пусть ряд
 сходится
в точке
сходится
в точке  .
Тогда этот ряд сходится абсолютно в
круге
.
Тогда этот ряд сходится абсолютно в
круге 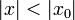 и
равномерно по
и
равномерно по  на
любом компактном
подмножестве этого
круга.
на
любом компактном
подмножестве этого
круга.
Обращая
эту теорему, получаем, что если степенной
ряд расходится при ![]() ,
он расходится при всех
,
он расходится при всех ![]() ,
таких что
,
таких что ![]() .
Из первой теоремы Абеля также следует,
что существует такой радиус
круга
.
Из первой теоремы Абеля также следует,
что существует такой радиус
круга ![]() (возможно,
нулевой или бесконечный), что при
(возможно,
нулевой или бесконечный), что при ![]() ряд
сходится абсолютно (и равномерно по
ряд
сходится абсолютно (и равномерно по ![]() на
компактных подмножествах круга
на
компактных подмножествах круга ![]() ),
а при
),
а при ![]() —
расходится. Это значение
—
расходится. Это значение ![]() называется
радиусом сходимости ряда, а круг
называется
радиусом сходимости ряда, а круг ![]() —
кругом сходимости.
—
кругом сходимости.
Степенные ряды по степеням (x-a).
![]() - ряд разложен в окрестности точки a.
- ряд разложен в окрестности точки a.
![]() -
ряд разложен в окрестности точки
-
ряд разложен в окрестности точки
![]() .
.
![]()
![]()
![]()
Способы определения R степенного ряда.

Для определения радиуса сходимости можно применить известные признаки Даламбера или Коши.
Признак Даламбера:

Если
 равен конечному числу L,
тогда
равен конечному числу L,
тогда

Данный ряд является сходящимся, если
![]() для любых
для любых
![]() -
ряд сходиться, причем сходиться абсолютно
в интервале
-
ряд сходиться, причем сходиться абсолютно
в интервале
![]() .
Т.е. при
.
Т.е. при
![]() ,
а при
,
а при
![]() .
.
 Аналогично и для определения радиуса
по признаку Коши:
Аналогично и для определения радиуса
по признаку Коши:
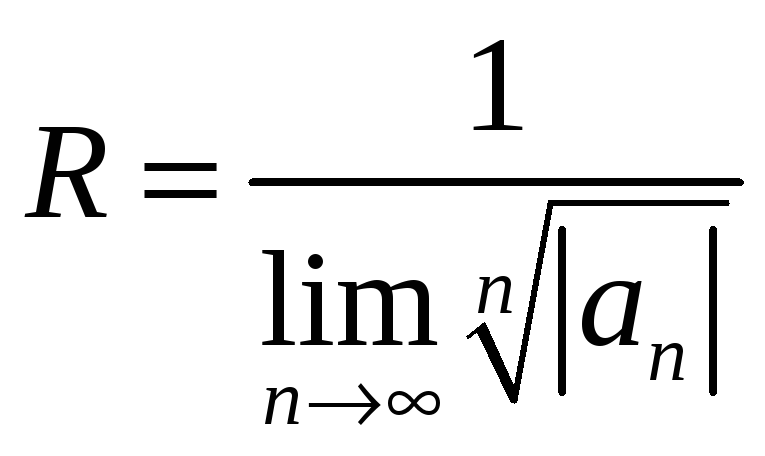
|
Дифференцирование и интегрирование степенных рядов |
|
Рассмотрим
степенной ряд
Функция Степенной ряд внутри интервала сходимости можно дифференцировать почленно. При этом производная степенного ряда выражается формулой
Степенной ряд можно также почленно интегрировать на отрезке, который расположен внутри интервала сходимости. Следовательно, если − R < b < x < R, то выполняется равенство
Если ряд интегрируется на отрезке [0; x], то справедлива формула:
|

 ,
имеющий радиус сходимости R
> 0:
,
имеющий радиус сходимости R
> 0: является
непрерывной функцией при |x|
< R.
является
непрерывной функцией при |x|
< R.