HaoZip RAR Архив_1 / ЛЕКЦИЯ 10

ЛЕКЦИЯ 10

Ряды с произвольными членами

Рассмотрим знакопеременные ряды, т. е. ряды, у которых бесконечно много как положительных, так и отрицательных членов.

Наряду со знакопеременным рядом (8)

будем рассматривать ряд, составленный из абсолютных величин

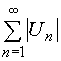. (9)

Теорема 11. Достаточный признак сходимости знакопеременного ряда. Если сходится ряд , то сходится и ряд , причём абсолютно.

Доказательство. Составим частичные суммы каждого из рядов:

S_n — n-ая частичная сумма ряда (8),

_п — п-ая частичная сумма ряда (9).

Пусть

S_n1 — сумма всех положительных слагаемых суммы S_n;

S_n2 — сумма абсолютных величин оставшихся (отрицательных) слагаемых, входящих в S_n.

Тогда

 

Но по условию ряд (9) сходится и, следовательно, существует его сумма

Вывод: последовательности частичных сумм {S_n1} и {S_n2} – возрастающие, но ограничены сверху (их пределы конечны). Вспоминая теорему о возрастающей, ограниченной последовательности, можем утверждать, что существует предел

т. к. существует каждый из пределов

  

Из этой теоремы имеем практический вывод: при исследовании сходимости ряда (8) можно исследовать сначала ряд (9). Если последний сходится, то и ряд (8) сходится.

Исследовать сходимость ряда .

Решение. Ряд — знакопеременный. Составим ряд из абсолютных величин

.

Последний ряд знакоположительный, причём  Сравним его со сходящимся рядом  (эталонный ряд (4)):

.

По признаку сравнения (см. Теорему 6) наш знакоположительный ряд сходится. Тогда по теореме 11 исходный ряд также сходится, причём абсолютно.

Определение. Ряд с произвольными членами называется абсолютно сходящимся, если сходится ряд . Если же ряд сходится, а ряд 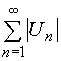 расходится, то говорят, что ряд  сходится условно.

Сходящийся ряд  называется сходящимся абсолютно, если сходится ряд из модулей , иначе — сходящимся условно.

Аналогично, если несобственный интеграл  от функции сходится, то он называется сходящимся абсолютно или условно в зависимости от того, сходится или нет интеграл от ее модуля .

Признаки абсолютной сходимости[править | править исходный текст]

Признак сравнения[править | править исходный текст]

Если  при , то:

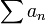• если ряд  сходится, то ряд  сходится абсолютно

• если ряд  расходится, то ряд  расходится

Согласно критерию Коши, . Значит, 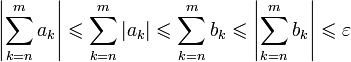, и по критерию Коши ряд  сходится. Второе утверждение следует из первого, так как если бы ряд сходился, то и ряд  сходился бы.

Признак сходимости рядов с монотонно убывающими членами[править | править исходный текст]

Пусть . Тогда ряд  сходится тогда и только тогда, когда сходится ряд 

Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:

Признак Лейбница[править | править исходный текст]

Основная статья: Теорема Лейбница о сходимости знакочередующихся рядов

Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:

Пусть для знакочередующегося ряда выполняются следующие условия:  (монотонное убывание {an}) . Тогда этот ряд сходится.

Если, выполнены все условия, и ряд из модулей () сходится, то исходный ряд сходится абсолютно. Если выполнены все условия, но ряд из модулей расходится, то исходный ряд сходится условно. Строгая положительность  существенна.

Ряды, удовлетворяющие признаку Лейбница, называются рядами Лейбница. Следует отметить, что этот признак является достаточным, но не необходимым.

Пример

. Ряд из модулей имеет вид  — это гармонический ряд, который расходится.

Теперь воспользуемся признаком Лейбница:

1. знакочередование выполнено 

2. 

3. .

Следовательно, так как все условия выполнены, но ряд из модулей расходится, искомый ряд сходится условно.

Условная Сходимость.

Ряд  называется условно сходящимся, если сам он сходится, а ряд, составленный из абсолютных величин его членов, расходится. То есть, если  существует (и не бесконечен), но .

Примеры[править | править исходный текст]

Простейшие примеры условно сходящихся рядов дают убывающие по абсолютной величине знакочередующиеся ряды. Например, ряд

сходится лишь условно, так как ряд из его абсолютных величин — гармонический ряд — расходится.