
HaoZip RAR Архив_1 / ЛЕКЦИЯ 7
.docЛЕКЦИЯ 7
Система дифференциальных уравнений
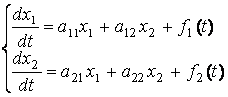 ,
,
где ![]() - искомые
функции от t;
- искомые
функции от t; ![]() - постоянные
числа;
- постоянные
числа; ![]() -
заданные
-
заданные
функции, называется системой линейных дифференциальных уравнений с постоянными коэффициентами второго порядка.
Такую систему методом исключения можно привести к одному линейному урав-нению не выше второго порядка. Решение этой задачи рассмотрим на примерах.
Пример
1 
Дифференцируем
первое уравнение по t :  .
Подставляем сюда из
.
Подставляем сюда из
системы уравнений производные ![]() :
:
 . Из
первого уравне-ния системы
. Из
первого уравне-ния системы ![]() , тогда
, тогда 
![]()
![]() . Т
.о.,
. Т
.о.,  -
линейное уравнение; решая его
известным способом, найдем
-
линейное уравнение; решая его
известным способом, найдем ![]() ; далее,
; далее, ![]() находим
из со-отношения
находим
из со-отношения ![]()
![]() . Общее
решение системы :
. Общее
решение системы :
 .
.
Решим
задачу Коши с начальными данными
: ![]() .
.
![]()
![]()
![]() .
.
 .
.
|
Линейные системы дифференциальных уравнений с переменными коэффициентами |
|
|
|
Нормальная линейная система дифференциальных уравнений с переменными коэффициентами записывается в виде
где xi (t) − неизвестные функции, которые являются непрерывными и дифференцируемыми на некотором интервале [a, b]. Коэффициенты aij (t) и свободные члены fi (t) представляют собой непрерывные функции, заданные на интервале [a, b]. Используя векторно-матричные обозначения, данную систему уравнений можно записать как
где
В общем случае матрица A(t) и вектор-функции X(t), f(t) могут принимать как действительные, так и комплексные значения. Соответствующая однородная система с переменными коэффициентами в векторной форме имеет вид
|
Привести к каноническому виду систему дифференциальных уравнений
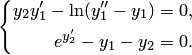
Решение. Данная
система имеет третий порядок, так
как ![]() и,
значит,
и,
значит, ![]() .
Разрешая первое уравнение относительно
.
Разрешая первое уравнение относительно ![]() ,
а второе относительно
,
а второе относительно ![]() ,
получим каноническую систему
,
получим каноническую систему
![]()
Система обыкновенных дифференциальных уравнений первого порядка вида
![]()
|
(3) |
где ![]() —
независимая переменная;
—
независимая переменная; ![]() —
неизвестные функции от
—
неизвестные функции от ![]() ,
называется нормальной
системой.
,
называется нормальной
системой.
Число ![]() называется порядком
нормальной системы (3).
Две системы дифференциальных уравнений
называются эквивалентными,
если они обладают одними и теми же
решениями.
называется порядком
нормальной системы (3).
Две системы дифференциальных уравнений
называются эквивалентными,
если они обладают одними и теми же
решениями.
Любую каноническую систему (2) можно привести к эквивалентной ей нормальной системе (3), причем порядок этих систем будет одним и тем же.
Задачей Коши для системы (3) называется задача нахождения решения
![]()
этой системы, удовлетворяющего начальным условиям
![]()
|
(4) |
где ![]() —
заданные числа.
—
заданные числа.
Теорема существования и единственности решения задачи Коши.
Пусть
имеем нормальную систему дифференциальных
уравнений (3) и пусть функции ![]()
![]() ,
определены в некоторой n+1-мерной
области
,
определены в некоторой n+1-мерной
области ![]() изменения
переменных
изменения
переменных ![]() .
Если существует окрестность
.
Если существует окрестность ![]() точки
точки ![]() ,
в которой функции
,
в которой функции ![]() а)
непрерывны, 6) имеют ограниченные частные
производные по переменным
а)
непрерывны, 6) имеют ограниченные частные
производные по переменным ![]() ,
то найдется интервал
,
то найдется интервал ![]() изменения
изменения ![]() ,
в котором существует единственное
решение нормальной системы (3),
удовлетворяющее начальным условиям
(4).
,
в котором существует единственное
решение нормальной системы (3),
удовлетворяющее начальным условиям
(4).
Система ![]() дифференцируемых
функций
дифференцируемых
функций
![]()
|
(5) |
независимой
переменной ![]() и
и ![]() произвольных
постоянных
произвольных
постоянных ![]() называется
общим решением нормальной системы (3),
если: 1) при любых допустимых
значениях
называется
общим решением нормальной системы (3),
если: 1) при любых допустимых
значениях ![]() система
функций (5) обращает уравнения (3) в
тождества, 2) в области, где выполняются
условия теоремы Коши, функции (5) решают
любую задачу Коши.
система
функций (5) обращает уравнения (3) в
тождества, 2) в области, где выполняются
условия теоремы Коши, функции (5) решают
любую задачу Коши.
Частным случаем канонической системы дифференциальных уравнений является одно уравнение n-го порядка, разрешенное относительно старшей производной.
![]()
Введением новых функций
![]()
это
уравнение заменяется нормальной
системой ![]() уравнений
уравнений
Можно
утверждать и обратное, что, вообще
говоря, нормальная система ![]() уравнений
первого порядка эквивалентна
одному уравнению порядка
уравнений
первого порядка эквивалентна
одному уравнению порядка ![]() .
На этом основан один из методов
интегрирования систем дифференциальных
уравнений — метод
исключения.
Проиллюстрируем
этот метод на примере системы двух
уравнений:
.
На этом основан один из методов
интегрирования систем дифференциальных
уравнений — метод
исключения.
Проиллюстрируем
этот метод на примере системы двух
уравнений:
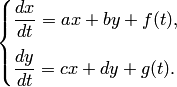
|
(1) |
Здесь ![]() —
постоянные коэффициенты, а
—
постоянные коэффициенты, а ![]() и
и ![]() —
заданные функции;
—
заданные функции; ![]() и
и ![]() —
искомые функции. Из первого уравнения
системы (1) находим
—
искомые функции. Из первого уравнения
системы (1) находим
![]()
|
(2) |
Подставляя
во второе уравнение системы вместо у
правую часть (2), а вместо ![]() производную
от правой части (2), получаем уравнение
at второго порядка относительно
производную
от правой части (2), получаем уравнение
at второго порядка относительно ![]()
![]()
где ![]() —
постоянные. Отсюда находим
—
постоянные. Отсюда находим ![]() .
Подставив найденное выражение для
.
Подставив найденное выражение для ![]() и
и ![]() в
(2), найдем
в
(2), найдем ![]() .
.
Нормальная линейная система дифференциальных уравнений с постоянными коэффициентами n-го порядказаписывается в виде
![]()
где x1(t), x2(t), ..., xn(t) − неизвестные функции переменной t, которая часто имеет смысл времени,aij − заданные постоянные коэффициенты, которые могут быть как действительными, так и комплексными,fi (t) − заданные (в общем случае комплексные) функции переменной t. Будем считать, что все указанные функции являются непрерывными на некотором интервале [a, b]действительной числовой оси t. Полагая

систему дифференциальных уравнений можно переписать в матричной форме:
![]()
Если
вектор f(t) тождественно
равен нулю: ![]() ,
то система называется однородной:
,
то система называется однородной:
![]()
Однородные системы уравнений с постоянными коэффициентами можно решать различными способами. Чаще всего используются следующие методы решений:
-
метод исключения (метод сведения системы n уравнений к одному уравнению n-го порядка);
-
метод интегрируемых комбинаций;
-
метод собственных значений и собственных векторов (включая метод неопределенных коэффициентов или использование жордановой формы в случае кратных корней характеристического уравнения);
-
метод матричной экспоненты.
Ниже на данной странице мы обсудим детально метод исключения. Другие способы решения систем уравнений рассматриваются отдельно на соответствующих страницах.
Метод исключения
Используя метод исключения, нормальную линейную систему n уравнений можно привести к одному линейному уравнению n-го порядка. Этот метод удобно использовать для решения простых систем − прежде всего, для систем 2-го порядка. Рассмотрим однородную систему двух уравнений с постоянными коэффициентами:

где функции x1, x2 зависят от переменной t. Продифференцируем первое уравнение и подставим производную x2' из второго уравнения:
![]()
Из первого уравнения подставим a12x2. Получаем линейное однородное уравнение 2-го порядка:

Его решение легко построить, если известны корни характеристического уравнения:
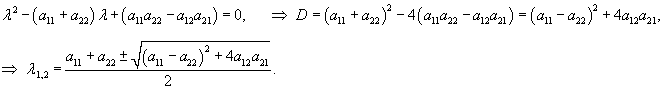
В случае действительных коэффициентов aij корни могут быть как действительными (различными или кратными), так и комплексными. В частности, если коэффициенты a12 и a21 одного знака, то дискриминант характеристического уравнения всегда будет положительным и, соответственно, корни будут действительными и различными. После определения функции x1(t) другую функцию x2(t) можно найти из первого уравнения системы. Метод исключения можно применять не только к однородным линейным системам. Его можно использовать также для решения неоднородных систем дифференциальных уравнений или систем уравнений с переменными коэффициентами.
Собственные векторы и собственные значения
Пусть A – матрица некоторого линейного преобразования порядка n. Определение. Многочлен n-ой степени
P()=det(A-Е) (1.1)
называется характеристическим многочленом матрицы А, а его корни, которые могут быть как действительными, так и комплексными, называются характеристическими корнями этой матрицы. Определение. Ненулевой вектор x линейного пространства V, удовлетворяющий условию
А(х)=х, (1.2)
называется собственным вектором преобразования A. Число называется собственным значением. Замечание. Если в пространстве V задан базис, то это условие можно переписать следующим образом:
Ах=х, (1.3)
где A – матрица преобразования, x – координатный столбец. Определение. Алгебраической кратностью собственного значения jназывается кратность корня j характеристического многочлена. Определение. Совокупность всех собственных значений называетсяспектром матрицы.
Алгоритм нахождения собственных значений и собственных векторов
-
Найти собственные значения матрицы:
-
записать характеристическое уравнение:
det(A-Е)=0; (1.4)
-
найти его корни j, j=1,...,n и их кратности.
Найти собственные векторы матрицы:
-
для каждого j решить уравнение
(A- jE)x=0; (1.5)
-
найденный вектор х и будет собственным вектором, отвечающим собственному значению j.
Линейная однородная система дифференциальных уравнений с постоянными коэффициентами
![]()
![]()

![]()
![]()
В векторной форме:
dY/dx = AY,
где
![]()
![]()

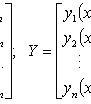

Характеристическое уравнение
![]()
![]()

![]()
![]()
или ![]()
![]() .
.

