HaoZip RAR Архив_1 / ЛЕКЦИЯ 12

ЛЕКЦИЯ 12

Ряды Тейлора и Маклорена.

Ряды Тейлора и Маклорена для основных элементарных функций.

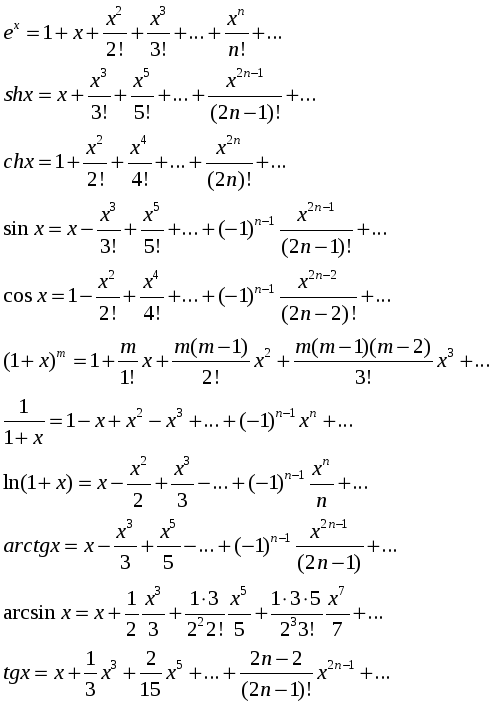
Разложение функций в степенные ряды. Ряд Тейлора

Общая постановка задачи разложения функции в ряд в комплексной области формулируется так же, как и в действительной области. А именно, для заданной функции , определенной в области  и удовлетворяющий в ней него которым дополнительным условиям, требуется найти ряд вида  который бы сходился в области  и его сумма в этой области совпадала с .

Постановка задачи разложения функции в степенной ряд

Для функции , аналитической в области , найти ряд , сходящийся к  в круге , принадлежащем области , то есть

(3.15)

Равенство (3.15) означает, что  является суммой ряда в круге .

Для решения задачи нужно, очевидно, найти коэффициенты ряда по заданной функции ; найти круг сходимости ряда и установить сходимость ряда именно к . Последнее, напомним, означает, что для точек круга выполняется неравенство  для любого  и .

Все поставленные вопросы решаются с помощью следующей теоремы.

Теорема Тейлора о разложении функции в степенной ряд

Теорема 3.4. Функция, аналитическая в области , в окрестности каждой точки  этой области представляется в виде степенного ряда (3.15), радиус сходимости  которого не меньше, чем расстояние от точки  до границы области . Коэффициенты ряда вычисляются по формуле

(3.16)

где  — произвольный контур, принадлежащий области  и охватывающий точку , в частности,  — окружность  или по формуле

(3.17)

На основании теоремы можно сформулировать алгоритм решения поставленной выше задачи и вывод — утверждение.

Необходимое и достаточное условие разложения функции в ряд Тейлора

Разберем задачу, которая является противоположной той, которая была расмотрена ранее. Предположим, что функцияв т.. Допустим, функцияявляется бесконечно дифференцируемой, если, при этомследовательно для нее ряд Маклорена будет таким:

 

.

 Если, то его сумма. Определим каковы должны быть условия, чтобы

О: В качестве многочлена Тейлора степенипонимают частичную сумму

 

 Остаточный член ряда Тейлора есть

 

(30.8)

 Т: Если требуется, чтобы бесконечно дифференцируемая в т.была представлена в качестве суммы составленного для нее ряда Тейлора (30.6), необходимо и достаточно выполнение следующго условия

 

.

В соответствии с определением сходящегося ряда и используя выражение (30.8), запишем такую цепочку:

 

- сумма (30.6)

.

 

Представим запись остаточного члена, выраженного в форме Лагранжа:

 

 

в данном случаерасполагается междуи.

Применение степенных рядов к приближенным вычислениям.

Вычисление значений функций.

Пусть f(x) является суммой ряда Тейлора ( 13 ). Необходимо с погрешностью  определить значение функции в точке х1 из области сходимости ряда (x0 – R, x0 + R). Для этого определим номер n при котором значение остаточного члена |Rn(x1)| равно указанной погрешности  и вычислим значение многочлена Тейлора Sn(x1)

Вычислить интеграл , где область R ограничена параболами и гиперболами . Замена переменных в двойных интегралах

Пр. Вычислить число е с точностью до 0,001

В разложении ( 14 ) положим х = 1 : е = 1 + 1 + 1/2! + . . . + 1/n! + . . .

Согласно ( 13 ) Rn(1) = exp()/ (n+1)! , а exp() < exp(1) < 3 , т.е. = Rn(1)< 3/(n+1)!

При n = 5 имеем < 3/6! = 1/240 > 0.001 , а при n = 6   < 3/7! = 1/1680 < 0.001

Поэтому е = 2 + ½! + 1/3! + ¼! + 1/5! + 1/6! = 2.7181 с точностью до 0,001.

Применение степенных рядов к приближенным вычислениям.

Вычисление значений функций.

Пусть f(x) является суммой ряда Тейлора ( 13 ). Необходимо с погрешностью  определить значение функции в точке х1 из области сходимости ряда (x0 – R, x0 + R). Для этого определим номер n при котором значение остаточного члена |Rn(x1)| равно указанной погрешности  и вычислим значение многочлена Тейлора Sn(x1)

Вычислить интеграл , где область R ограничена параболами и гиперболами . Замена переменных в двойных интегралах

Пр. Вычислить число е с точностью до 0,001

В разложении ( 14 ) положим х = 1 : е = 1 + 1 + 1/2! + . . . + 1/n! + . . .

Согласно ( 13 ) Rn(1) = exp()/ (n+1)! , а exp() < exp(1) < 3 , т.е. = Rn(1)< 3/(n+1)!

При n = 5 имеем < 3/6! = 1/240 > 0.001 , а при n = 6   < 3/7! = 1/1680 < 0.001

Поэтому е = 2 + ½! + 1/3! + ¼! + 1/5! + 1/6! = 2.7181 с точностью до 0,001.

Вычисление определенных интегралов с помощью рядов

 

Мы уже отмечали, что некоторые интегралы не могут быть вычислены, то есть, выражены в элементарных функциях.

Для их нахождения могут быть использованы разложения подынтегральных функций в степенные ряды, которые сходятся очень быстро.

Рассмотрим несколько примеров:

Пример 1.

Пусть требуется вычислить интеграл .

Здесь первообразная не является элементарной функцией. Поэтому, для вычисления этого интеграла, разложим подынтегральную функцию в ряд, заменяя в разложении e^x показатель x на –x² , итак

e^x=1+ x+ + . . .

.

         Интегрируя обе части этого равенства в пределах от 0 до a, получим:

 

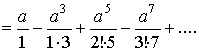
Получившийся степенной ряд сходится и требуемое его значение можно вычислить с наперед заданной точностью, зная, что погрешность не превосходит по величине первого отбрасываемого члена данного степенного ряда.

Пусть a=1 и нужна точность 0,001, тогда

,

т. е. необходимо учитывать только шесть первых членов полученного ряда.