HaoZip RAR Архив_1 / ЛЕКЦИЯ 6

ЛЕКЦИЯ 6

Неоднородные дифференциальные уравнения высшего порядка с постоянными коэффициентами

Данные уравнения имеют вид где a1, a2,..., an − действительные или комплексные числа, а правая часть f(x) является непрерывной функцией на некотором отрезке [a, b].  Используя линейный дифференциальный оператор L(D), равный неоднородное дифференциальное уравнение можно записать в виде Общее решение y(x) неоднородного уравнения представляется в виде суммы общего решения y0(x)соответствующего однородного уравнения и частного решения y1(x)  неоднородного уравнения: При произвольной правой части f(x) для поиска общего решения неоднородного уравнения используетсяметод вариации постоянных. В случае, если правая часть представляет собой произведение многочлена и экспоненциальной функции, частное решение удобнее искать методом неопределенных коэффициентов.

Принцип суперпозиции

Для линейных неоднородных уравнений справедлив принцип суперпозиции, который формулируется следующим образом. Пусть правая часть f(x) представляет собой сумму двух функций:

Предположим, что y₁(x) является решением уравнения

а функция y₂(x) является, соответственно, решением второго уравнения

Тогда сумма функций

будет являться решением линейного неоднородного уравнения

Метод вариации постоянных

Предположим, что общее решение однородного дифференциального уравнения n-го порядка известно и представляется формулой

Метод вариации постоянных (или метод Лагранжа) заключается в том, что вместо постоянных чисел C₁,C₂,..., C_n мы рассматриваем функции C₁(x), C₂(x),..., C_n(x). Эти функции подбираются таким образом, чтобы решение

удовлетворяло исходному неоднородному уравнению.  Производные n неизвестных функций C₁(x), C₂(x),..., C_n(x) определяются из системы n уравнений:

Определителем этой системы является вронскиан функций Y₁, Y₂,..., Y_n, образующих фундаментальную систему решений. В силу линейной независимости этих функций определитель не равен нулю и данная система однозначно разрешима. Окончательные выражения для функций C₁(x), C₂(x),..., C_n(x) находятся в результате интегрирования.

Доказано, что для линейного неоднородного дифференциального уравнения  y⁽ⁿ⁾ + a₁ y^(n-1) + ... + a_n-1 y' + a_n y = f(x) при непрерывной правой части f(x), для любых начальных значений  x₀,  y₀,   y_0,1, ..., y_0,n-1  существует и единственно решение задачи Коши  y(x₀)=y₀, (y)'(x₀)=y_0,1 , ...,(y)^(n-1)(x₀)=y_0,n-1.

Решение задачи Коши для неоднородного дифференциального уравнения с постоянными коэффициентами можно найти методом вариации произвольных постоянных (методом Лагранжа), который состоит в следующем:  Записываем искомое решение задачи Коши для неоднородного уравнения  в виде  y(x)= c₁(x) y₁(x) +  c₂(x) y₂(x) + ... + c_n(x) y_n(x), где  y₁(x),  y₂(x), ..., y_n(x)  — линейно независимые решения соответствующего однородного уравнения, и находим неизвестные функции c₁(x) ,  c₂(x), ...,  c_n(x), такие, чтобы функция y = y(x) удовлетворяла неоднородному уравнению и заданным начальным условиям.

Опишем алгоритм решения задачи Коши для уравнения второго порядка y'' + a₁ y' + a₂ y = f(x), y(x₀)=y₀, (y)'(x₀)=y_0,1.  Будем искать решение задачи в виде y(x)= c₁(x) y₁(x) +  c₂(x) y₂(x),  где  y₁(x),  y₂(x) — линейно независимые решения однородного уравнения y'' + a₁ y' + a₂ y = 0. Вычислим  y'(x), y''(x)  и подставим полученные выражения в уравнение.  Вычислим первую производную y'(x)= (c₁'(x) y₁(x) +  c₂(x)' y₂(x)) + (c₁(x) y₁'(x) +  c₂(x) y₂'(x)),  положим  c₁'(x) y₁(x) +  c₂(x)' y₂(x)  = 0 и тогда  y'(x)= c₁(x) y₁'(x) +  c₂(x) y₂'(x), y''(x)= (y'(x))'= (c₁(x) y₁'(x) +  c₂(x) y₂'(x))'= =c₁'(x) y₁'(x) +  c₂(x)' y₂'(x) + c₁(x) y₁''(x) +  c₂(x) y₂''(x).

 

Подставив y(x) и ее производные в уравнение, получим: y'' + a₁ y' + a₂ y = = c₁'(x) y₁'(x) +  c₂(x)' y₂'(x) + c₁(x) y₁''(x) +  c₂(x) y₂''(x) +  + a₁(c₁(x) y₁'(x)+c₂(x) y₂'(x)) + a₂(c₁(x) y₁(x)+c₂(x) y₂(x)) = = c₁(x)( y₁''(x)+a₁ y₁'(x)+a₂ y₁(x)) + c₂(x)( y₂''(x)+a₁ y₂'(x)+a₂ y₂(x)) + + c₁'(x) y₁'(x) +  c₂(x)' y₂'(x) = 0 + 0 + c₁'(x) y₁'(x) +  c₂(x)' y₂'(x) = f(x), при условии c₁'(x) y₁(x) +  c₂(x)' y₂(x)  = 0.

Тогда неизвестные функции c₁(x) и c₂(x) являются решениями системы линейных дифференциальных уравнений  c₁'(x) y₁'(x) +  c₂(x)' y₂'(x) =  f(x), c₁'(x) y₁(x) +  c₂(x)' y₂(x)  = 0 с известными y₁(x) и y₂(x). Эта система легко разрешима относительно c₁(x) и c₂(x): c₁'(x) =  f(x)y₂(x)/(y₁'(x)y₂(x)-y₁(x)y₂'(x)), c₁'(x)= f(x)y₁(x)/(y₁(x)y₂'(x)-y₁'(x)y₂(x)). Вычислив интегралы в правой части системы, получим

Произвольные константы C₁  и  C₂   определяются из начальных условий.

Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Структура общего решения Линейное неоднородное уравнение данного типа имеет вид: где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение: Теорема: Общее решение неоднородного уравнения является суммой общего решения y0(x) соответствуюшего однородного уравнения и частного решения y1(x) неоднородного уравнения: Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений.

Метод неопределенных коэффициентов

Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов.  Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как

1. 

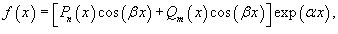2.   где P_n(x) и Q_m(x) − многочлены степени n и m, соответственно.

В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения.  В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель x^s, где s − кратность корня α в характеристическом уравнении.  В случае 2, если число α + βi совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x.  Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение.