Лекция 9 «Дифракционная решётка как спектральный прибор»

План лекции:

1. Краткий обзор предыдущих лекций.

1.1 Критерий типа дифракции.

1.2 Дифракция Фраунгофера от щели.

1.3 Многолучевая интерференция.

2. Дифракционная решётка как спектральный прибор.

3. Критерий Рэлея. Разрешающая способность дифракционной решётки.

Итог лекции 9

1. Краткий обзор предыдущих лекций

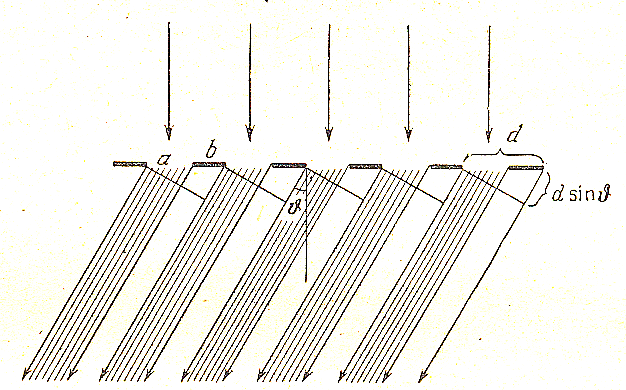
Дифракционная решётка представляет собой совокупность большого числа одинаковых, равностоящих параллельных щелей. Изготавливают решётки, нанося с помощью делительной машины штрихи на плоскую стеклянную или металлическую поверхность. Разные решётки содержат разное число штрихов на каждый миллиметр: от десятков до десятка тысяч. На рисунке 9.1 представлен фрагмент одномерной дифракционной решётки.

Рис. 9.1

Здесь b— ширина щели,d— расстояние между щелями. Это расстояние называется «постоянная решётки» (период). Речь здесь идёт, конечно, о пространственной периодичности, но не о временной.

Теперь рассмотрим плоскую световую волну, падающую на дифракционную решётку.

Свет будет дифрагировать на каждой щели. Далее за решёткой волны, идущие от всех щелей, при наложении интерферируют.

Таким образом мы встречаемся с двумя задачами, каждую из которых мы ранее подробно рассматривали.

Это: 1 — дифракции Фраунгофера на щели и

2 — многолучевая интерференция.

Освежим в памяти выводы, к которым мы пришли, решая эти задачи.

0. Критерии типа дифракции (см. Лекцию №8).

Различают два типа дифракции:

1) Дифракцию сферических волн, или дифракцию Френеля

2) Дифракцию плоских волн — дифракцию Фраунгофера.

На прошлой лекции был получен безразмерный численный параметр, определяющий тип дифракции от щели: .

Было показано, что если этот параметр много меньше единицы, наблюдается дифракция Фраунгофера. Когда он порядка единицы, — дифракция Френеля.

— дифракция Фраунгофера;

— дифракция Френеля.

Мы будем изучать работу дифракционной решётки при условии дифракции Фраунгофера.

0. Дифракция Фраунгофера от щели (см. Лекцию №8).

При дифракции Фраунгофера от щели «b» на экране наблюдения возникает дифракционная картина (рис. 9.2) чередующихся максимумов и минимумов.

Рис. 9.2

Было установлено, что интенсивность света является функцией угла дифракции φ:

(9.1)

Отсюда нетрудно получить условия минимумов:

b sinφ = ± k λ (k = 1, 2, 3...) (9.2)

0. Многолучевая интерференция (см. Лекцию №6).

Складывая когерентные волны, излучаемые равноотстоящими точечными синфазными источниками (рис. 6.1), мы получим закон распределения интенсивности в дальней волновой зоне (6.8):

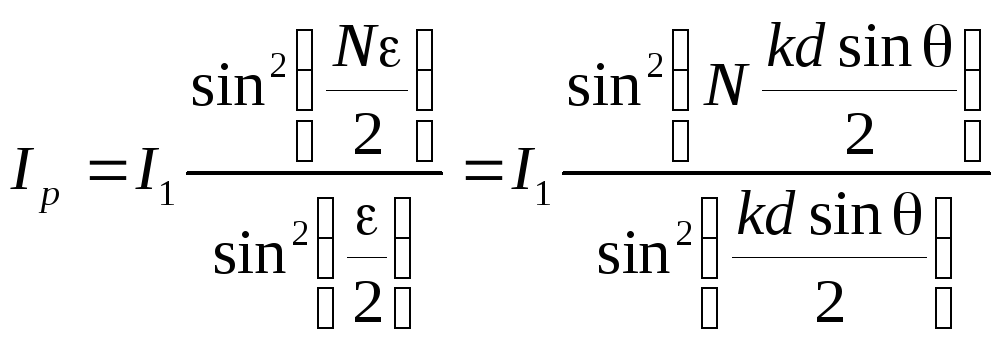(9.3)

Здесь: I_p — результирующая интенсивность в направлении θ,

I₁ — интенсивность в точке наблюдения от одного источника,

N — число источников.

Анализ уравнения (6.8) (или - что то же самое – 9.3) позволил выявить направления θ_max, в которых результирующая интенсивность принимает максимальное значение. Это так называемое условие максимумов:

(9.4)

Здесь: λ — длина волны излучения, d—расстояние между источниками.

2. Дифракционная решётка как спектральный прибор

Пусть на решётку падает нормально плоская монохроматическая волна (λ). С тем, чтобы оставаться в рамках дифракции Фраунгофера, за решёткой поместим собирающую линзу, а в её фокальной плоскости — экран наблюдения (рис. 9.3).

Рис. 9.3

Ясно, что распределение интенсивности на экране от одной щели будет определятся только направлением дифрагировавших лучей. Это означает, что дифракционные картины, создаваемые на экране любой отдельной щелью, будут совершенно одинаковы, независимо от положения щели на решётке (см. 9.1).

Теперь сложим Nтаких волн, дифрагировавших на щелях решётки.Результат сложения двух волн, пришедших через соседние щели, будет определятся разностью хода Δ = d sinφ. Суммарную интенсивность, возникшую от сложения N подобных волн, запишем в виде уравнения (9.3):

.(9.5)

где: ε = k d sinφ — разность фаз волн, приходящих от двух соседних щелей.

Объединив выражение (9.1) и (9.5), получим окончательное распределение интенсивности света за дифракционной решёткой.

. (9.6)

Здесь: I₀ — интенсивность, создаваемая одной щелью против центра линзы,

b — ширина щели,

N — число щелей,

d — период (постоянная) решётки.

Проанализируем полученный результат(9.6).

1. Интенсивность обращается в ноль, когда

bsinφ = ±kλ, (k= 1, 2, 3...) (9.7)

Это известное условие минимумовпри дифракции от щели (9.2).

2. В направлениях φ, удовлетворяющих условию

dsinφ = ±mλ, (m= 0, 1, 2, 3...), (9.8)

будут наблюдаться главные интерференционные максимумыпри наложенииNволн. Это условие максимумов многолучевой интерференции (см. (9.4)). В этих направлениях волны от всехNщелей решетки приходят к точке наблюдения в фазе, поэтому их амплитуды складываются. Результирующая амплитуда:A_рез=N A_φ.

Интенсивность пропорциональна квадрату амплитуды, поэтому

I_реш(φ) =N ²I_щ(φ). (9.9)

Здесь: I_щ(φ) — интенсивность света, дифрагировавшего от одной щели в направлении φ.

Между двумя соседними главными максимумами располагаются (N – 1) промежуточный минимум. Эти минимумы делят расстояние между главными максимумами наNчастей. Картина распределения интенсивности за дифракционной решёткой дляN= 4 и, приведена на рис. 9.4. Пунктирная кривая изображает здесь интенсивность от одной щели, умноженную наN ².

Рис. 9.4.

Число главных максимумов вытекает из (9.8):

Угол между направлениями на два минимума, ограничивающих главный максимум, называется угловой шириной максимума.

Подсчитаем, например, угловую ширину нулевого максимума (см. рис. 9.4)

(9.10)

Дифракционные решётки широко используются в качестве спектральных приборов благодаря тому, что положение главных максимумов за решёткой зависит от длины волны λ:

(9.11)

Если на решётку падает смесь двух волн: λ и (λ + δ λ), то их нулевые максимумы, конечно, совпадут, ноm-ые максимумы окажутся в разных точках экрана.

Условие m-го максимума волны λ:,

а волны (λ + δ λ): .

Таким образом, появляется возможность разложить с помощью дифракционной решётки смесь волн в спектр и измерить длины волн, входящих в смесь, либо их частоты.