
- •Часть 2. (Повышенный уровень) Перевод дробной части.
- •Часть 3. Перевод из х2 в х8 и из х2 в х16.
- •Часть 4. Перевод из х8 в х16 и из х16 в х8.
- •Часть 5. Сложение в разных системах счисления.
- •Часть 6. (Дополнительная) Вычитание в различных системах счисления.
- •Часть 7. Вычитание с переводом в дополнительный код.
- •Часть 2. (Повышенный уровень) Переведите числа и их дробные части.
- •Часть 9. Построение скнф.
- •Часть 10. Построение сднф.
- •Часть 7. Выполните вычитание с переводом в дополнительный код.
- •Часть 8. Составить таблицы истинности для следующих функций:
- •Часть 9. Постройте скнф и сднф для каждой из следующих таблиц истинности:
Часть 9. Построение скнф.
|
Для того, чтобы получить СКНФ функции, требуется составить её таблицу истинности.
В
ячейках строки́ Четвёртая строка содержит 0 в указанном поле. Отмечаются значения всех четырёх переменных, это: x1=0; x2=0; x3=1; x4=1; В дизъюнкцию записывается переменная без инверсии, если она в наборе равна 0, и с инверсией, если она равна 1. Первый член СКНФ рассматриваемой функции выглядит так:
Остальные члены СКНФ составляются по аналогии. Далее записывается конъюнкция элементарных дизъюнкций. |
Часть 10. Построение сднф.
|
Для того, чтобы получить СКНФ функции, требуется составить её таблицу истинности.
В
ячейках строки́ Третья строка содержит 1 в указанном поле. Отмечаются значения всех четырёх переменных, это: x1=0; x2=0; x3=1; x4=0; В дизъюнкцию записывается переменная без инверсии, если она в наборе равна 1, и с инверсией, если она равна 0. Первый член СДНФ рассматриваемой функции выглядит так:
Остальные члены СКНФ составляются по аналогии. Далее записывается дизъюнкция элементарных конъюнкций. |
Задания:

 отмечаются
лишь те комбинации, которые приводят
логическое выражение в состояние
нуля.
отмечаются
лишь те комбинации, которые приводят
логическое выражение в состояние
нуля.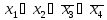
 отмечаются
лишь те комбинации, которые приводят
логическое выражение в состояние
единицы.
отмечаются
лишь те комбинации, которые приводят
логическое выражение в состояние
единицы.