Домашняя работа к семинару 27.11.13

Часть 1. Перевод из Х₁₀->Х_2,8,16.

Правило: Для того, чтобы перевести целое десятичное число в другую систему счисления, необходимо осуществлять последовательное деление десятичного числа и затем получаемых целых частных на основание той системы, в которую оно переводится, до тех пор, пока не получится частное, меньшее делителя. Число в новой системе записывается в виде остатков от деления, начиная с последнего.

Пример:

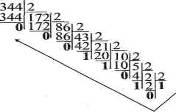
Перевести число 344 из десятичной в двоичную: Ответ: 1010110002.

Перевести число 936 из десятичной системы в шестнадцатеричную. Ответ: 3A816.

Часть 2. Перевод из Х_2,8,16->Х₁₀.

Правило: Для того, чтобы перевести число из другой системы счисления в десятичную, необходимо представить число в виде многочлена, представляющего из себя сумму произведений разряда числа и основания системы счисления в степени, равной номеру разряда. 

Пример:

Перевод из двоичной в десятичную:

Перевод из восьмиричной в десятичную:

Перевод из шестнадцатиричной в десятичную:

Часть 2. (Повышенный уровень) Перевод дробной части.

Правило: Для перевода дробной части необходимо разделить разряд числа на соответствующую ему степень разряда. Разряды после запятой нумеруются отрицательными числами по убыванию начиная с –1.

Пример:

Перевод дробной части двоичного числа в десятичную степень:

Перевод дробной части восьмеричного числа в десятичную степень:

Перевод дробной части шестнадцатеричного числа в десятичную степень:

Часть 3. Перевод из х2 в х8 и из х2 в х16.

Правило: Чтобы перевести число из двоичной системы в восьмеричную (шестнадцатеричную), его нужно разбить на триады (тетрады) (тройки(четверки) цифр, которые можно взять из таблицы), начиная с младшего разряда [справа налево], в случае необходимости дополнив старшую триаду (тетраду) нулями, и каждую триаду заменить соответствующей восьмеричной цифрой.

Для осуществления обратного перевода нужно заменить каждую цифру числа в восьмеричной (шестнадцатеричной) системе эквивалентной триадой (тетрадой) в двоичной и записать их последовательно.

Пример:

Перевод двоичного числа в восьмеричную:

Перевод числа из восьмеричной в двоичную: Перевод двоичного числа в шестнадцатеричную:

Перевод числа из шестнадцатеричной в двоичную:

Часть 4. Перевод из х8 в х16 и из х16 в х8.

Правило: Для перевода из Х₈ в Х₁₆ необходимо пользоваться таблицей систем счисления.

Алгоритм:

1. По таблице перевести нужное число из восьмеричной (шестнадцатеричной) двоичную систему.

[см. раздел 3]

2. По таблице перевести полученное двоичное число в шестнадцатеричную (восьмеричную) систему. [см. раздел 3]

Х10	Х2	Х8	Х16
0	00	0	0
1	01	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	А
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

Пример:

Часть 5. Сложение в разных системах счисления.

Правило: Сложение чисел в любой позиционной системе счисления выполняется поразрядно. Для нахождения суммы складываются единицы одного и того же разряда, начиная с единиц первого разряда (справа). Если сумма единиц складываемого разряда превышает число, равное основанию системы, то из этой суммы выделяется единица старшего разряда, которая и добавляется к соседнему разряду слева. Поэтому сложение можно производить непосредственно, как и в десятичной системе, в "столбик", используя таблицу сложения однозначных чисел.

! Для проведения арифметических операций над числами, выраженными в различных системах счисления, необходимо предварительно перевести их в одну и ту же систему.

При сложении в столбик соответствующие разряды записываются друг под другом.

Пример:

	Таблица сложения в двоичной системе: В последнем случае пишем 0, а единица переносится в старший разряд.
	4 пишем, 1 переносится в старший разряд плюс 1 в запасе => //запись сверху математически неверна, но так проще считать;
	4 пишем, а 1 переносится в старший разряд. ! так как в 16й системе нет 16, а есть только 15, то 16-15=1. 1 пишем, а еще 1 единица переносится в старший разряд.