Arkhiv_v_pomosch / Минимизация скнф сднф
.docxЧасть 11. Минимизация СКНФ, СДНФ.
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:
Аналогично для КНФ:
Возможность поглощения следует из очевидных равенств
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей.
Карты Карно.
Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ, могут иметь в своём составе 2N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:
Часть 12. Полином Жегалкина.
Метод неопределенных коэффициентов
Построение полинома Жегалкина
Существует несколько способов построения полинома Жегалкина.
[править]
По таблице истинности
Пусть
для функции
задана таблица истинности. Запишем
сначала данную функцию в виде полинома
Жегалкина с неопределёнными коэффициентами.
Затем по очереди подставляем всевозможные
наборы в порядке увеличения количества
единиц и находим коэффициенты с учётом
того, что
,
а
.
За каждую подстановку находим только
один коэффициент.
Пример:
Дана функция
и её таблица истинности:
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
Построим для неё полином Жегалкина:
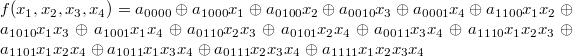
Так
как
,
то
.
Далее подставляем все остальные наборы
в порядке возрастания числа единиц,
подставляя вновь полученные значения
в следующие формулы:
Таким образом, полином Жегалкина выглядит так:
Преобразование дизъюнктивной нормальной формы
Этот
способ основан на том, что
.
Если функция задана в виде ДНФ, то можно
сначала убрать дизъюнкцию, используя
правило Де-Моргана, а все отрицания
заменить прибавлением единицы по модулю
два, после чего раскрыть скобки по
обычным правилам, при этом учитывая,
что четное число одинаковых слагаемых
равно нулю (так как
),
а нечетное число одинаковых слагаемых
равно одному такому слагаемому. Либо
же можно заменить дизъюнкцию по следующему
правилу:
.
Если функция задана в СДНФ, то так как при любых значениях входных переменных в единицу обращается не более одного члена выражения, то достаточно просто заменить все дизъюнкции исключающим ИЛИ.
Пример:
Дана функция в ДНФ
,
построим полином Жегалкина.
Запишем функцию так:
;
Сгруппируем слагаемые и воспользуемся преобразованием (1):
Воспользуемся
свойствами конъюнкции
и
,
а также тем, что
,
и упростим выражение:
Ещё раз воспользуемся преобразованием (1):
Раскроем скобку по алгебраическим правилам:
Снова воспользуемся свойствами конъюнкции и исключающего ИЛИ:
Заменим
отрицание на прибавление
:
Раскроем скобки:
Выкинем парные слагаемые и получим окончательную формулу:
