
Конспект лекций по КМР
.pdf
Чувствительность – способность рабочего органа исполнительного устройства робота отклоняться от заданного положения при
изменении обобщенных координат на малую величину |
qi : |
||||
|
r |
x y z |
|
, |
(2.17) |
|
n |
|
|||
|
|
|
|
|
|
|
|
qi |
|
|
|
|
|
i 1 |
|
|
|
где x, y, z |
– линейные отклонения координат x, y, z; |
|
|||
, ,
– угловые отклонения координат
, ,
.
Чувствительность для одной и той же структурной схемы исполнительного устройства робота зависит от длин i звеньев. Чем
длиннее звенья, тем больше чувствительность. Таким образом, при одном и том же значении
qi
одинаковые
структурные, но разные кинематические схемы исполнительного устройства робота обладают разной чувствительностью.
2.3. Кинематические характеристики
Мобильность – способность ХРТ рабочего органа исполнительного устройства робота двигаться в заданной точке рабочей зоны с требуемой скоростью.
Для кинематической схемы исполнительного устройства робота
с заданными максимальной |
|
и минимальной |
|
qi( j,k) max |
qi( j,k) min |
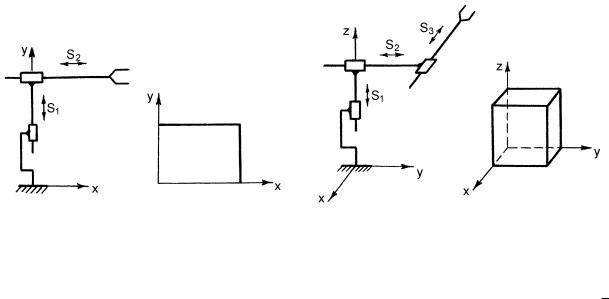
обобщенными скоростями каждой точке С из области возможных обобщенных скоростей соответствует точка D в области возможных скоростей рабочего органа (рис. 2.7).
Рис. 2.7
51

Мобильность определяют по формуле:
|
M |
n |
|
|
f j |
fk qi |
q j qk |
, |
|||
|
fi |
||||||||||
|
|
|
|
T |
T |
T |
|
|
|
|
|
|
|
i( j,k ) |
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
где fi( j,k) – столбец матрицы Якоби |
|
|
|
|
|
||||||
|
|
|
|
F q |
F q |
F |
q |
|
|
||
|
T |
|
|
|
1 |
2 |
|
3 |
|
; |
|
|
fi( j,k) |
|
q |
q |
|
q |
|
|
|||
|
|
|
|
|
|
||||||
Fi q |
|
|
|
|
i( j,k) |
i( j,k ) |
i( j,k ) |
|
|
||
– i-я координата заданной точки D рабочей зоны |
|||||||||||
|
F1 q xD ; |
F2 q yD |
; F3 q zD |
; |
|
||||||
xD , yD , zD – координаты заданной точки D; |
|
|
|
||||||||
qi( j,k ) |
– обобщенная координата i(j,k)-й степени подвижности; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
qi( j,k) – диапазон изменения i(j,k)-й обобщенной скорости |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qi( j,k) qi( j,k) max qi( j,k) min ; |
|
||||||||
(2.18)
(2.19)
qi( j,k) max
и |
|
qi( j,k) min |
– максимальное и минимальное значения
обобщенной скорости.
Обобщенная скорость может быть положительной и отрицательной. Для углового движения обобщенную скорость считают положительной, если она направлена против хода часовой стрелки и отрицательной – по ходу часовой стрелки.
n – число перестановок из m степеней подвижности исполнительного устройства робота по три числа i, j, k (для двухстепенного исполнительного устройства по два числа i, j), удовлетворяющих условию
1 i j k n . |
|
(2.20) |
Следует отметить, что в двух- и трехстепенных исполнительных |
||
устройствах роботов в формуле (2.18) знак |
|
пропадает, так как |
|
||
составить перестановки из двух элементов по два или из трех элементов по три, удовлетворяющих условию (2.20), возможно единственным способом i=1, j=2 или i=1, j=2, k=3.
Для четырехстепенного исполнительного устройства робота в |
||
формуле (2.18) знак |
|
сохраняется, так как возможно составить из |
|
||
четырех элементов по три, удовлетворяющих условию (2.20), четы-
ре перестановки: i=1, j=2, k=3; i=1, j=2, k=4; i=1, j=3, k=4; i=2, j=3, k=4.
Для пяти- и шестистепенных исполнительных устройств роботов число перестановок значительно возрастает.
Чем больше мобильность, тем выше скоростные возможности исполнительного устройства робота в заданной точке.
52
2.4. Технические характеристики
Номинальная грузоподъемность mн (кг) – наибольшее значение массы m объекта вместе с массой захватного устройства mз, при которой гарантируется его захватывание, удержание и обеспечение установленных значений эксплуатационных характеристик робота:
mн = m + mз.
В проектных расчетах, когда масса захватного устройства неизвестна, номинальную грузоподъемность можно определить по формуле:
mн = Кс Кп m,
где Кc=1,3...1,4 – коэффициент, учитывающий массу захватного устройства; Кп – коэффициент, учитывающий тип привода. Для пневматического привода Кп=1,3, гидравлического – Кп=1,1, для вакуумного и магнитного – Кп=1,15.
Число степеней подвижности W исполнительного устройства робота – число управляемых обобщенных координат.
Диапазоны перемещений по степеням подвижности: линейные Si, мм; угловые i, рад.
Максимальные скорости перемещения по степеням подвижно-
сти: линейные vmax, м/с; угловые wmax, рад/с. В отечественных промышленных роботах:
vmax
0,6... |
1,0 |
м/с,
wmax
1,5...3,0
рад/с.
|
Максимальные ускорения по степеням подвижности: линейные |
||
a |
, м/с2, угловые |
max |
, рад/с2. |
max |
|
|
|
|
Структурная схема исполнительного механизма – схема, ука- |
||
зывающая основание (стойку), подвижные звенья, виды кинематических пар и их взаимное расположение.
Тип системы координат: прямоугольная, полярная и ангулярная (угловая).
Движения исполнительного устройства робота: ориентирующие (локальные) – движения, предназначенные
для придания рабочему органу необходимой ориентации в заданной точке рабочей зоны;
53
транспортирующие (региональные) – движения, предназначенные для перемещения рабочего органа в различные точки рабочей зоны;
координатные (глобальные) – движения, обеспечивающие перемещение исполнительного устройства между отдельными производственными позициями на расстояния, превышающие обычно как размеры самого робота, так и размеры обслуживаемого им оборудования и рабочего места.
54
Глава 3 КИНЕМАТИКА РОБОТОВ
3.1.Системы координат роботов
Взависимости от типа кинематической схемы исполнительного механизма робота движения рабочего органа осуществляются в различных системах координат: прямоугольной (Декартовой), полярной и ангулярной (угловой). Система координатных перемещений определяет кинематику транспортирующих движений исполнительного устройства робота и форму его рабочей зоны.
Прямоугольная (Декартова) система координат. Прямоугольную систему координат делят на два вида:
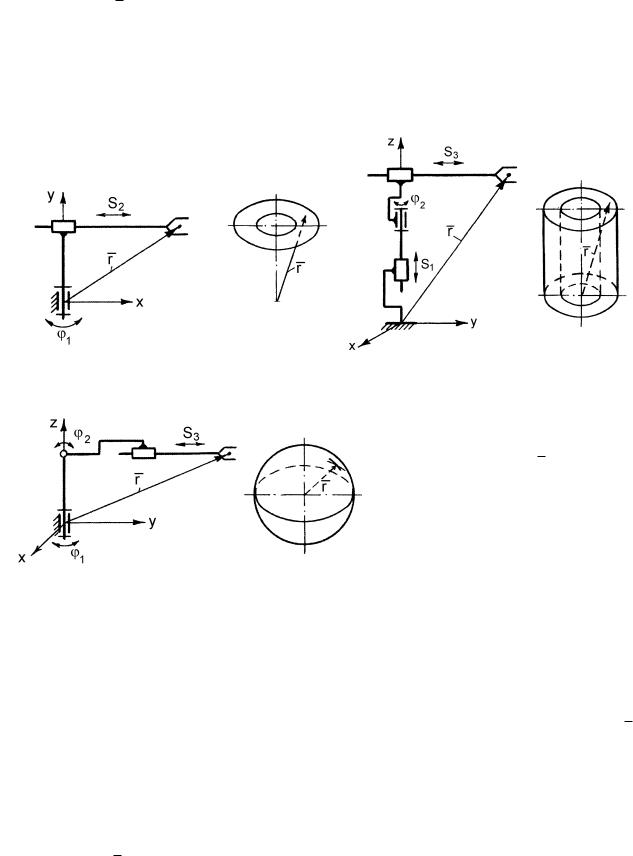
1.Прямоугольная плоская – характеризуется перемещением рабочего органа по двум взаимноперпендикулярным осям (рис. 3.1, а). На рис. 3.1, б показана рабочая зона с которой может совпадать рабочий орган исполнительного устройства при его функционировании.
2.Прямоугольная пространственная – характеризуется перемещением рабочего органа по трем взаимноперпендикулярным осям. На рис. 3.2, а показана структурная схема исполнительного механизма промышленного робота «Versaweld» (Англия) и его рабочая зона (рис. 3.2, б).
а) |
б) |
а) |
б) |
|
Рис. 3.1 |
|
Рис. 3.2 |
Полярная система координат. Она бывает трех видов:
1. Полярная плоская – характеризуется радиус-вектором r , изменяющимся в зависимости от линейного перемещения рабочего органа вдоль одной оси и углового перемещения вокруг другой взаимноперпендикулярной оси. Структурная схема исполнительного механизма робота и его рабочая зона изображены на рис. 3.3, а, б соответственно.
55
2.Полярная цилиндрическая – характеризуется радиус-
вектором r , изменяющимся в зависимости от линейных перемещений рабочего органа вдоль двух взаимноперпендикулярных осей и углового перемещения вокруг одной из указанных осей. Структурная схема исполнительных механизмов промышленных роботов «ПР-10И» и «МП-9С» приведена на рис. 3.4, а, а их рабочая зона – на рис. 3.4, б.
а) |
б) |
|
а) |
|
|
б) |
Рис. 3.3 |
|
|
|
Рис. 3.4 |
|
|
|
|
|
3. |
Полярная |
сфериче- |
|
|
|
|
ская – характеризуется ра- |
|||
|
|
|
диус-вектором |
r |
, изменя- |
|
|
|
|
ющимся в зависимости от |
|||
|
|
|
линейного перемещения ра- |
|||
|
|
|
бочего |
органа |
вдоль одной |
|
|
|
|
оси и угловых перемещений |
|||
а) |
|
б) |
вокруг двух других взаимно- |
|||
|
перпендикулярных осей. На |
|||||
Рис. 3.5 |
|
|
||||
рис. 3.5,а показана структурная схема промышленного робота «Unimate» (США), а на рисунке 3.5,б – его рабочая зона.
Ангулярная (угловая) система координат. Она может быть трех видов:
1.Ангулярная плоская – характеризуется радиус-вектором r , изменяющимся в зависимости от относительных угловых перемещений звеньев исполнительного механизма в одной координатной плоскости. Структурная схема исполнительного механизма робота
иего рабочая зона приведены на рис. 3.6, а, б соответственно.
2.Ангулярная цилиндрическая – характеризуется радиус-
вектором r , изменяющимся в зависимости от относительных угловых перемещений звеньев исполнительного механизма в одной ко-
56

ординатной плоскости и их линейного перемещения вдоль оси, перпендикулярной рассматриваемой координатной плоскости (плоскости вращения звеньев). Структурная схема исполнительного механизма промышленного робота «SCARA» изображена на рис. 3.7, а, а его рабочая зона – на рис. 3.7, б.
а) |
б) |
а) |
б) |
|
Рис. 3.6 |
|
Рис. 3.7 |
3.Ангулярная сферическая
–характеризуется радиус-
вектором |
r |
, изменяющимся |
в |
|
|||
зависимости |
от |
относительных |
|
||||
угловых |
перемещений |
звеньев |
|
||||
исполнительного |
механизма |
в |
|
||||
двух взаимноперпендикулярных |
а) |
||||||
плоскостях. На рис. 3.8, а приве- |
|||||||
|
|||||||
дена структурная схема испол- |
|
||||||
нительного |
механизма |
промышленных |
|||||
«PUMA» (Финляндия), а на рис. 3.8, б –
б)
Рис. 3.8
роботов «РМ-01» (РФ), их рабочая зона.
3.2. Системы координат звеньев
Прежде чем рассматривать движения звеньев исполнительного устройства робота необходимо выбрать системы координат (СК), связанные с ними. В качестве таких систем координат могут быть использованы декартовы системы координат.
Инерциальную декартову систему координат, связанную с основанием (стойкой) исполнительного устройства робота называют базовой системой координат (БСК).
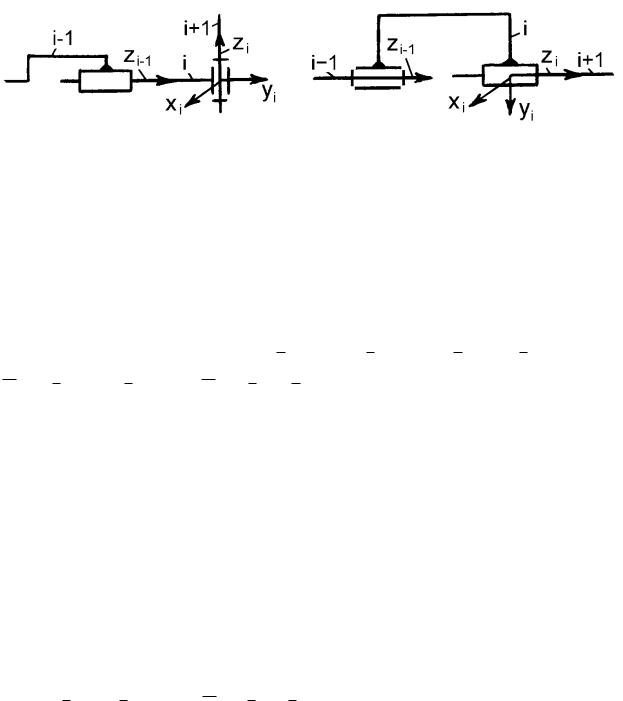
Декартова система координат, связанная с подвижным звеном исполнительного устройства робота представляет собой локальную систему координат звена (ЛСК). ЛСК связывают со звеном i (i=1...N) по следующему правилу (рис. 3.9):
57
а) |
б) |
Рис. 3.9
–ось Zi (i=1...N–1) направляют по оси кинематической пары, связывающей звенья i и i+1;
–ось Хi направляют перпендикулярно к осям Zi-1 и Zi, а также так, чтобы она пересекала ось Zi-1;
–ось Yi направляют перпендикулярно осям Хi и Zi и она должна обеспечить правую ориентацию всей системы координат.
Следует отметить, что ось Хi получают как векторное произве-
дение единичных векторов eZ (i 1) и |
eZ i или eZ i и eZ (i 1) , т.е. |
Xi eZ (i 1) eZ i или Xi eZ i eZ (i 1) , |
и направлена она перпенди- |
кулярно осям Zi-1 и Zi, а также так, чтобы при взгляде на стрелку оси Хi кратчайший поворот оси Zi-1 к оси Zi происходил против хода часовой стрелки.
Если оси Zi-1 и Zi параллельны, но не лежат на одной прямой, или (i-1)-я и i-я кинематические пары вращательные, то ось Хi направляют по оси звена, связывающего (i-1)-ю и i-ю кинематические пары.
В случае невозможности провести в i-й кинематической паре ось Хi так, чтобы она одновременно была перпендикулярна осям Zi-1 и Zi и пересекала ось Zi-1, то начало Оi i-й ЛСК нужно располагать не в конце i-го звена, а в начале, т.е. в (i-1)-й кинематической паре.
Ось Yi |
получают как векторное произведение единичных век- |
торов eZ i и |
eX i , т.е. Yi eZ i eX i , и направлена она перпендику- |
лярно осям Zi и Хi, а также так, чтобы при взгляде на стрелку оси Yi кратчайший поворот оси Zi к оси Хi происходил против хода часовой стрелки.
Для выбора системы осей координат рабочего органа на нем выбирают характеристическую рабочую точку (ХРТ) Р. Точка Р может и не принадлежать рабочему органу. Выбор этой точки чаще всего определяется технологическим назначением робота и связан с типом рабочего органа. Затем мысленно соединяют рабочий орган (звено N) в ХРТ со следующим условным N+1 звеном вращатель-
58

ной или поступательной кинематической парой, причем, если предыдущая кинематическая пара была поступательная, то и кинематическую пару рабочего органа выбирают поступательную (рис. 3.10, а), вращательная – вращательную (рис. 3.10, б, в).
а) |
б) |
в) |
Рис. 3.10
После этого направление осей системы координат, связанной с рабочим органом, выбирают по общему правилу, указанному выше.
Для удобства описания ориентации рабочего органа с ХРТ связывают вектор единичной длины, называемый характеристическим радиус-вектором (ХРВ), и вектор единичной длины нормальный к ХРВ, называемый нормальным радиус-вектором (НРВ). ХРВ и НРВ задают плоскость, положение которой полностью определяет ориентацию рабочего органа.
Для описания перемещений рабочего органа или последнего звена в ХРТ вводят еще один единичный вектор, нормальный к ХРВ и НРВ, называемый бинормальным радиус-вектором (БРВ). Тройка ХРВ, НРВ и БРВ образуют декартову систему координат рабочего органа, у которой ось Zn+1 представляет собой ХРВ, Yn+1
– НРВ и Хn+1 – БРВ. Каждая i-я ЛСК может быть определена в БСК через координаты ее начала Оi или проекции ее единичных ортов.
Координаты точек Оi определяют положения звеньев и рабочего органа, а проекции единичных ортов – ориентацию звеньев и рабочего органа.
При таком выборе систем осей координат каждая i-я система координат связана с i-м звеном. Перемещение i-й ЛСК относительно (i–1)-й характеризует движение i-го звена относительно (i-1)-го. Это движение может быть либо вращением на угол i вокруг оси Zi-1, либо поступательным перемещением на величину Si, вдоль оси Zi-1.
Так как число подвижных звеньев исполнительного устройства робота равно числу кинематических пар 5 класса, то совокупность величин i и Si однозначно определяет положение исполнительного механизма в пространстве.
59
3.3. Преобразования декартовых координат
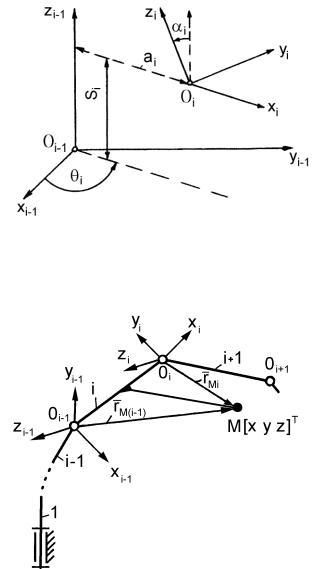
Взаимное положение систем координат двух соседних звеньев определяют 4 независимыми параметрами. В связи с этим систему координат (i–1)-го звена можно преобразовать в систему координат i-го звена с помощью четырех последовательно выполняемых преобразований (рис.
3.11) [18]:
а) поворот системы координат (i–1)-го звена вокруг оси Zi-1 на угол i до тех пор, пока оси Хi-1 и Хi не станут параллельными и направленными в одну сторону;
б) перенос системы координат (i–1)-го звена вдоль оси Zi-1 на величину Si до тех пор,
и Хi не совместятся (окажутся на одной прямой);
в) перенос системы координат (i–1)-го звена вдоль оси Хi на величину ai до совпадения начал систем координат
Оi-1 и Оi;
г) поворот системы координат (i–1)-го звена вокруг оси Хi на угол i до совмещения всех осей систем координат (i–1)-го и i-го звеньев.
Из четырех параметров i, Si, ai, i, определяющих переход от одной системы координат к другой, параметры ai и i
всегда постоянны и определяются конструкцией исполнительного устройства. Из двух других параметров ( i и Si) один является переменным и представляет собой функцию обобщенной координаты qi, соответствующей (i–1)-й кинематической паре, другой параметр постоянен:
для вращательной кинематической пары Si=const, i=f(qi)=var, для поступательной кинематической пары i=const, Si= f(qi)=var.
60
