Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технологический университет "Станкин"

Предмет:

Проектирование и конструирование машин и роботов

Файл:

Конспект лекций по КМР

.pdf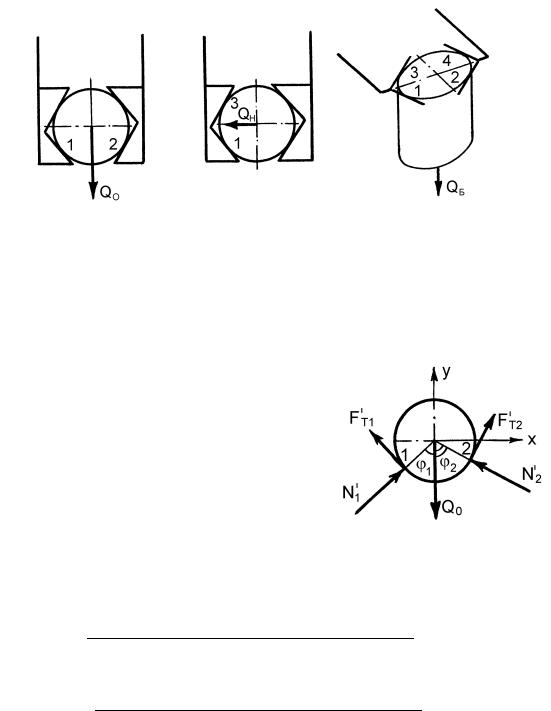

Скачиваний:

435

Добавлен:

11.02.2015

Размер:

19.54 Mб

Скачать

☆

<<< < Предыдущая 34 35 36 37 38 39 40 41 42 43 44 4546 / 6546 47 48 49 50 51 52 53 54 55 56 57 58 > Следующая >>>


захватного			устройства возникают нормальные			и касатель-
					N1, N2
ные			2	силы (рис. 14.17). Для их определения		рассмотрим
	FT	1, FT

равновесие объекта. Составим уравнения проекций всех сил на оси x и y:

а)	б)
	Рис. 14.16

N sin

F cos

N sin

y N cos

sin

cos

Касательная

сила

(сила

трения)

FT N f , где f – коэффициент трения

скольжения между объектом и рабочими

элементами. Для незакаленных сталей

без

насечки (стали

марок

45,

50)

f=0,12...0,15; для закаленных сталей с

острой насечкой (стали марок 65Г, У8А,

У10А) f=0,3...0,35.

После

подстановки

выражения

для

силы

FT в систему уравнений и ее ре-

в)


		cos 2		0;
FT2
	sin 2		Q0		0 .
FT2

Рис. 14.17

шения, найдем нормальные силы и силы трения, возникающие в точках контакта объекта с рабочими элементами:

sin 2

cos 2

1 f 2

sin 1 2 2 f cos 1

;

sin

f cos

sin

;

2 f

cos

N f

; F

f .

Если 1 2 , то нормальные силы будут равны:

(14.16)

(14.17)

(14.18)

406

							Q0			sin f				cos

									1 f 2 sin 2 2 f cos 2 .
		N1				N2			1 f 2 sin 2 2 f cos 2 .

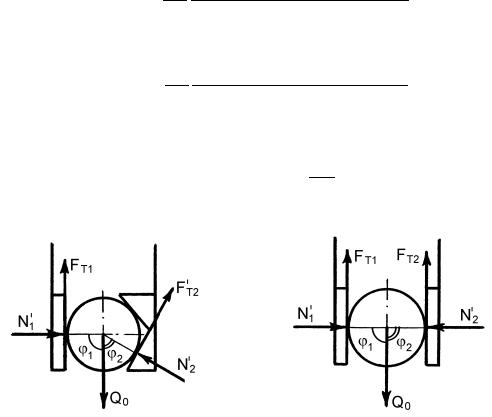
Если только					1	90		(рис. 14.18), то
Если только					1			(рис. 14.18), то
								Q		sin		2	f	cos				2
								0				2						2	;
						N1		2	f	sin			1		f	2	cos		;
																2
											2								2
											2								2
								Q					1
								0					1				cos		.
						N2		2	f	sin					f	2			.
																2
											2								2
											2								2

При	1		2	90			(рис. 14.19), получим:
При	1		2				(рис. 14.19), получим:
														Q
															0	.
										N1 N2				2 f		.
														2 f

(14.19)

(14.20)

(14.21)

(14.22)

Рис. 14.18 Рис. 14.19

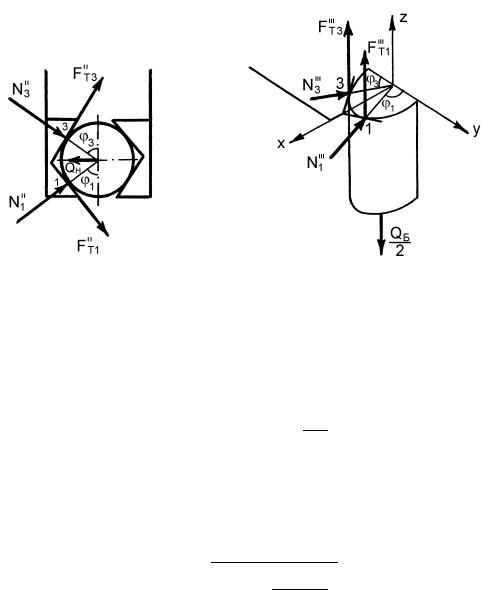
Для элементарной схемы (рис. 14.16, б) удержания объекта в точках 1 и 3 контакта объекта с рабочими элементами возникают

N ,

, F

нормальные

3 и касательные

T 1

T 3 силы (рис. 14.20).

Рассматривая равновесие объекта, найдем нормальные силы и

силы трения:

cos 3

f sin 3

QH 1 f 2 sin 1

3 2 f cos 1

3 ;

(14.23)

cos 1

f sin 1

QH 1 f 2 sin 1

3 2 f cos 1

3 .

(14.24)

При 1

90 :

и полная нормальная сила будет равна:

407

N N
1	3

(14.25)

Рис. 14.20 Рис. 14.21

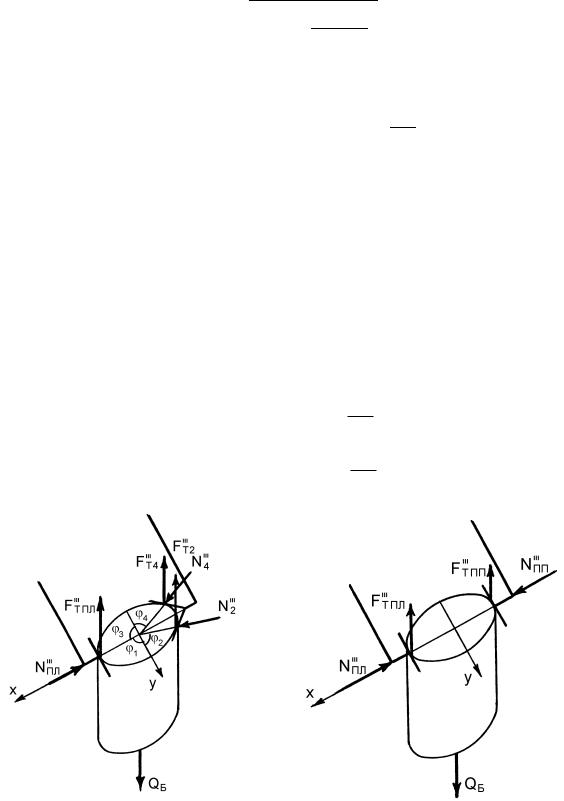
Для элементарной схемы (рис. 14.16, в) удержания объекта в точках 1,2, 3 и 4 контакта объекта с рабочими элементами возник-

нут нормальные	N , N , N ,			N	и касательные	F	, F	, F	, F
нут нормальные	1	2	3	4	и касательные	T1	T2	T3	T4

силы. Для их определения рассмотрим равновесие половинок объекта. Для левой половинки объекта (рис. 14.21):

N f N f
1	3

		Q
		Б
		Б
		2

;

	cos 1		cos 3 .
N1		N3

После решения системы уравнений найдем значения нормальных сил:

N		Q
N			Б
1			cos
			cos
	2 f 1
			cos
			cos

1 3

  

;

(14.26)

		QБ		.	(14.27)

N3			cos 3
			cos 3
	2 f 1
	2 f 1		cos 1
			cos 1
Рассматривая равновесие правой половинки объекта, анало-
гично найдем:
		QБ		;	(14.28)

N2			cos 2
			cos 2
	2 f 1
	2 f 1		cos 4
			cos 4

408

При

1	2	3	4
1	2	3	4
			N

		Q
			Б		.
			cos		.
2 f			cos
2 f	1			4
			cos
			cos	2
будем иметь:
N		N N				Q
N		N N				Б
2			3	4		4 f
						4 f

(14.29)

(14.30)

Из полученных формул при равенстве всех углов видно, что какое бы значение ни приобретали углы величины нормальных сил остаются неизменными.

Если 1	3		а 2		и 4		(рис. 14.22), то полная
		90		90		90

нормальная сила, действующая слева на объект равна:

N	N N	QÁ	.	(14.31)

ÏË	1 3	2 f

Если

				90
1	2	3	4

(рис. 14.23), то полные нормальные

силы, действующие слева и справа на объект равны:

N ÏË



N 1

N 2

N	Q
	Á
3	2 f

N	Q	Á

4	2 f

;

(14.32)

(14.33)

Рис. 14.22

Рис. 14.23

Значения полной нормальной силы и силы трения в каждой точке контакта объекта с рабочими элементами захватного устройства находят по формулам:

409

		n
N	i	N j ;
	i	i	(14.34)
		j I	(14.34)

FTi N i f ,

где i=1,2,3,4 – номер точки контакта объекта с рабочими элементами; j – номер элементарной нормальной силы и силы трения в i- й точке контакта; n=III – максимальное число элементарных нормальных усилий и сил трения в i-й точке контакта.

Максимальное значение нормальной силы будет в той точке, в которой действует наибольшее число элементарных нормальных сил.

В общем случае опасную точку контакта можно определить в зависимости от направления действия вектора внешней силы Q . Если вектор усилия Q проходит через квадрант, содержащий i-ю точку контакта, то она и будет опасной точкой. В рассматриваемом

случае вектор усилия

проходит через квадрант, содержащий

точку контакта 1, поэтому она и является опасной.

14.12. Усилие захватывания

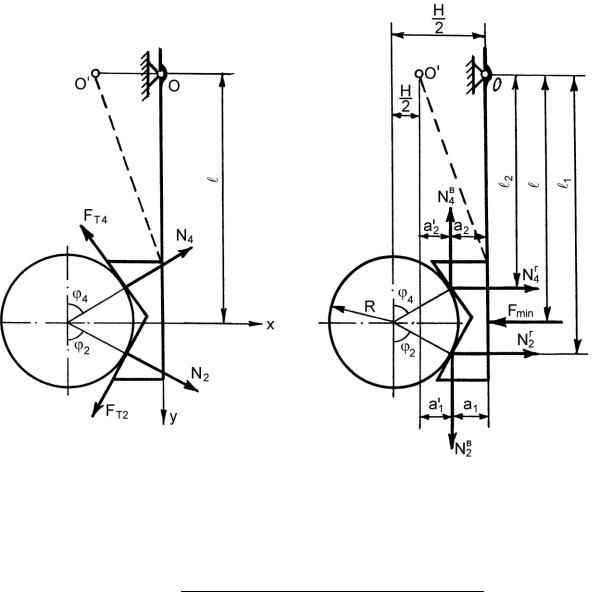
На каждый рабочий элемент захватного устройства в общем случае действует две полные нормальные силы и силы трения (рис. 14.24), которые направлены противоположно усилиям, действующим на объект.

Проецируя эти силы на направление, перпендикулярное к условной прямолинейной поверхности рабочего элемента (на ось х) и параллельное этой поверхности (на ось у), получим четыре силы, действующие на рабочий элемент захватного устройства (рис. 14.25):

N N	2	sin	2	F
2	2		2	T2

N N	4	sin	4	F
4	4		4	T4

N		N	2	cos			2	F
2								T2
N		N				cos
	4				4				4

cos

sin

FT4

2	;
4	;
2	;
sin
	4

Эти силы вызывают поворот рабочего элемента относительно точки О его вращения. Для уравновешивания рабочего элемента приложим в его середине усилие захватывания Fmin (рис. 14.25)

перпендикулярно условной прямолинейной поверхности на расстояние от точки вращения. Запишем уравнение моментов относительно точки О:

410

и N 4

411

N			N
	2	1

Рис. 14.24

	2	N B a		N B a
4		2	1	4	2

Fmin .

Рис. 14.25

Откуда найдем силу захватывания, которую необходимо приложить для уравновешивания рабочего элемента:

F	N	1	N	2	N B a		N B a
F	2	1	4	2	2	1	4	2
min

(14.35)

где 1 и 2 – плечо действия силы

N 2

N 4

соответственно:

	1	R cos	2	; 2	= – R cos 4; знак плюс ставят, если мо-

мент от вертикальной силы раскрывает рабочие элементы, знак минус – если закрывает; a1 и a2 – плечо действия силы N 2 соответственно:

	H		R sin 2		- если ЗУ раскрывается;

		2
a
1	R sin 2			H	- если ЗУ закрывается;

				2

			sin		H
	R		sin	4
a				4	2
a					2
2		H
		H	R sin
			R sin
	2				4
	2

-если ЗУ раскрывается;

-если ЗУ закрывается;

где R – радиус объекта; Н – расстояние между осями вращения рабочих элементов.

Следовательно, в общем случае при различном расположении оси вращения О или Оґ' рабочего элемента можно записать:

		N			R cos			N			R cos
F		N		2	R cos		2	N		4	R cos
F				2			2			4
min

N	B H				R sin		N
N	2				R sin	2	N	4	R sin			4
	2		2			2		4				4
			2

Сила Fmin является минимально необходимой,

которая требуется для удержания объекта. Для надежного закрепления объекта в рабочих элементах необходимо приложить усилие захватывания F больше минимального Fmin , т.е. F n Fmin , где n – коэффициент запаса равный 1,5...2,0.

Действие нормальных сил N i и сил трения FTi

на рабочий элемент можно условно заменить одной эквивалентной силой N min , приложенной в его

центре перпендикулярно условной поверхности и создающей тот же момент относительно точки О вращения, что и приложенные силы, и по величине равной N min Fmin (рис. 14.26) или с учетом коэффициента запаса N=F.

	4
	4
H

2

(14.36)

Рис. 14.26

14.13. Усилие привода

Усилие привода (сила Fвх или момент Твх) схвата определяют из условия равенства элементарных работ, совершаемых приводом (входным звеном преобразователя движения схвата) и рабочими

элементами, т.е.

AЉ

Mвх‰›

412

A
c
	. Откуда усилие привода равно:

KMвыхdLвых		KMвых вых	KMвых	,	(14.37)
		вх		,	(14.37)
	dLвх	вх	u

где Ад – работа, совершаемая приводом (работа движущих сил); Ас – работа, совершаемая рабочими элементами (работа сил сопротивления). Остальные параметры соответствуют параметрам в фор-

муле (14.1).

При преобразовании поступательного движения привода в поступательное движение рабочих элементов усилие привода определяют по формуле:

F	K N	dh	K N	v	ћ‰
F	K N		K N		ћ‰
пр		d		v
		d		v
				‰›

1 u

	Определим усилие					привода
	клинового	преобразователя					дви-
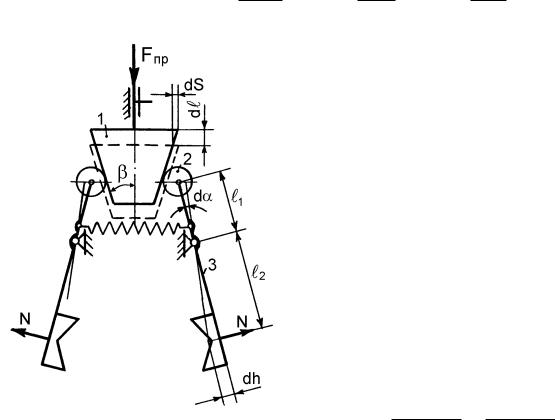
	жения схвата (рис. 14.27) при из-
	вестных эквивалентных силах N,
	действующих на рабочие элемен-
	ты.
	Находим передаточное						отно-
	шение преобразователя					движени-
	ия. Для этого дадим клину 1 эле-
	ментарное малое перемещение d .
	При этом ролик 2 переместится на
	малую величину dS, звено 3 – на
	элементарный угол d , а рабочий
	элемент – на величину dh.
	Элементарное		перемещение
	клина запишем в виде:
Рис. 14.27	d	dS		1	d		,
		tg	tg

где 1 – длина верхней части звена 2; – угол конуса клина; –

приведенный угол трения.						при осях на подшипниках
				1 10 –

качения и 3 – при осях на подшипниках скольжения.
Элементарное перемещение рабочего элемента равно:
		dh 2 d .
Находим передаточное отношение:
	u		d		1
							.
			dh		tg 2
Усилие привода определяем по формуле (14.37):
Fпр	K N			2 N 2		tg		,
	u				1

413

где =0,9...0,95 – КПД преобразователя движения.

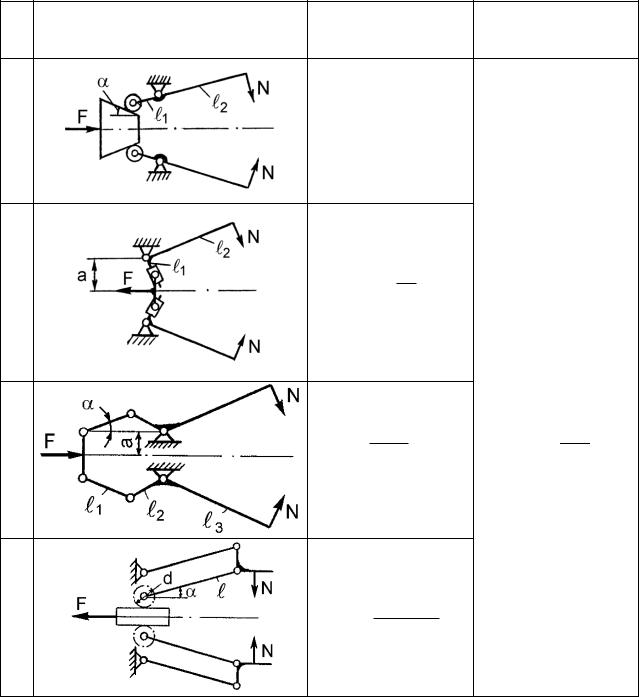
В табл. 14.2 представлены схемы преобразователей движения схватов и приведены расчетные формулы для определения передаточных отношений и усилий приводов.

Т а б л и ц а 14.2.

Силовые соотношения преобразователей движения схватов

№	Кинематическая схема	Передаточное	Усилие привода F
		отношение u

1	u		1
		2	tg

	u
	u

1 2

u	a	tg

	2	3

	F	2N
	F	u
		u

	u	d
	u	2 cos
		2 cos

414

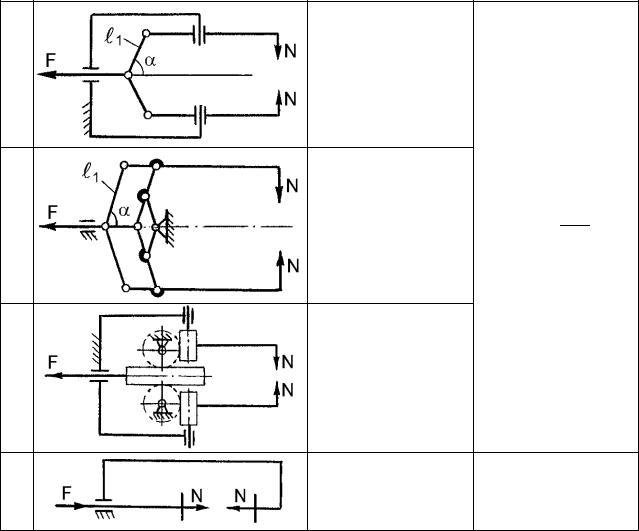
Продолжение табл. 14.2

u tg

u 1

	F	2N
	F	u
		u

F=N

Часто возникает необходимость при известном усилии привода определить усилие захватывания. Оно может быть определено по формуле (14.37) как обратное действие нахождению силы привода. По табл. 14.2 для приведенных схем преобразователей движения при известном усилие привода Fпр можно найти усилие захватыва-

ния N .

14.14. Усилия в выходных звеньях преобразователей движения

Из всего многообразия положений объекта в захватном устройстве можно выделить несколько основных схем (табл. 14.3): объект непосредственно поддерживается рабочими элементами, силы трения практически не участвуют в поддержании; объект удерживается за счет запирающего действия рабочих элементов при ограниченном действии сил трения; объект удерживается только силами трения.

415

<<< < Предыдущая 34 35 36 37 38 39 40 41 42 43 44 4546 / 6546 47 48 49 50 51 52 53 54 55 56 57 58 > Следующая >>>