Конспект лекций по КМР
.pdf

а) |
б) |
в) |
г) |
|
|
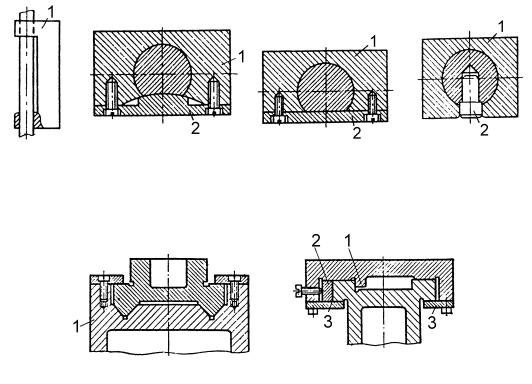
Рис. 13.2 |
|
а) |
б) |
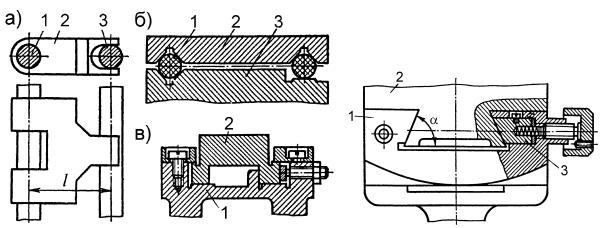
Рис. 13.3
В призматических направляющих применяют призмы 1 с трапециевидным (рис. 13.3, а), прямоугольным или треугольным сечением. Регулировку зазоров в направляющих проводят с помощью планок или «сухариков». На схеме (рис. 13.3, б) сдвиг направляющих в боковом направлении устраняют с помощью выступа 1 и планки 2, а вертикальное перемещение – с помощью двух планок 3. В направляющих, изображенных на рис. 13.1, г регулировку зазора проводят с помощью «сухариков» 3.
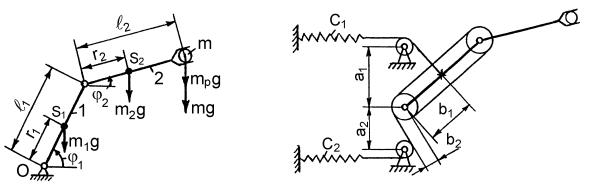
Для проверки правильности выбора посадки и класса точности сопрягаемых деталей направляющих проводят проверочный расчет по формуле [39]:
D1 1 1 t t0 D2 1 2 t t0 , |
(13.1) |
где – минимальный зазор при данной температуре, мм; D1 – наименьший при данном допуске диаметр (или линейный размер) охватывающей детали, мм; D2 – наибольший при данном допуске диаметр (или линейный размер) охватываемой детали, мм; t0 и t – соответственно начальная и конечная температура, град, направляющих; 1 и 2 – коэффициенты линейного расширения материалов сопрягаемых деталей (табл. 13.1).
364