Конспект лекций по КМР

В предварительных расчетах можно принять:

При b=a жесткость пружины будет минимальной:

Задаваясь параметрами a и b, можно вычислить жесткость пружины и все ее параметры.

Максимальная деформация пружины:

Максимальная сила упругой деформации пружины:

Потенциальная энергия пружины:

Полная потенциальная энергия пружины:

Рассмотрим основные схемы реальных уравновешивающих механизмов с синусно-косинусной нагрузочной характеристикой.

На рис. 12.14 изображены кулисные уравновешивающие механизмы.

Рис.12.14

347

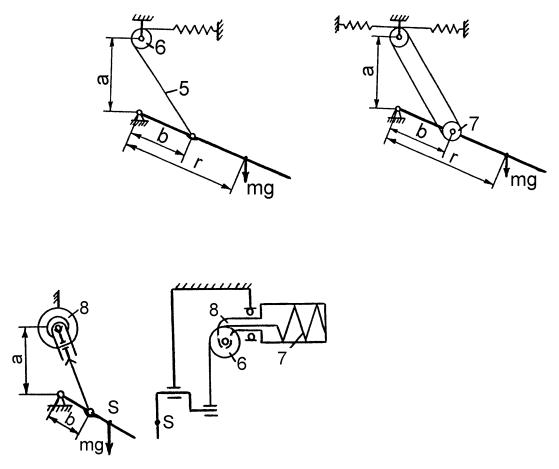
Они состоят из стойки 1, пружины 2, кривошипа 3, жестко соединенного с уравновешиваемым звеном 4, и кулисы 5. Эти механизмы обеспечивают теоретически точное воспроизведение нагрузочной характеристики, так как при повороте звена на любой уголсохраняется постоянство параметров a и b уравновешивающего механизма. Однако для работы кулисных механизмов требуется большое свободное пространство. Это обусловлено тем, что при повороте кулис вместе с ними должны поворачиваться и пружины, которые определяют основные габаритные размеры системы.

Указанный недостаток может быть устранен применением гибких элементов в сочетании с опорными роликами (рис. 12.15).Такими уравновешивающими механизмами являются механизмы, которые в отличие от расчетной схемы содержат дополнительно гибкий элемент 5 и опорный ролик 6. Однако при работе таких механизмов точка схода гибкого элемента с ролика перемещается, вызывая изменение угла обхвата ролика гибким элементом, что приводит к неточности воспроизведения нагрузочной характеристики (неточности уравновешивания).

348

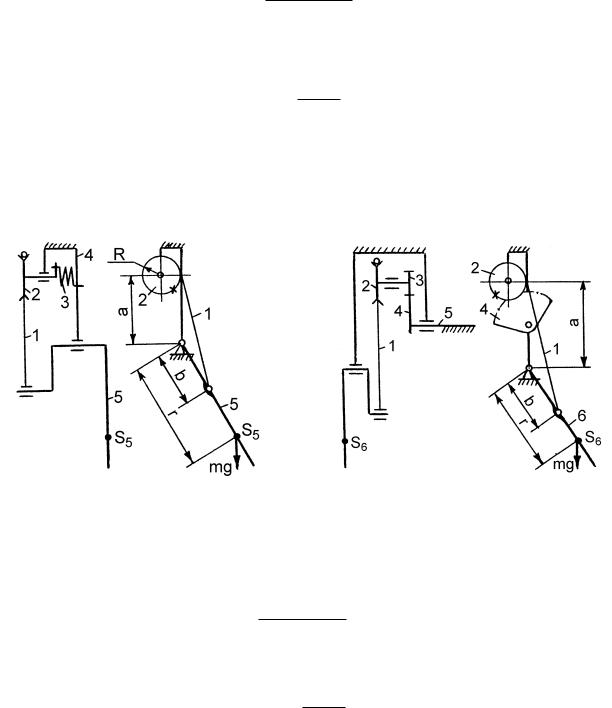
чения и торсионы. На рис. 12.18 изображен уравновешивающий механизм, состоящий из гибкого элемента 1, закрепленного на блоке 2, и пружины кручения 3, жестко соединенной с блоком 2 и стойкой 4. При изменении положения уравновешиваемого звена 5 происходит закручивание пружины. При этом крутящий момент пружины равен, Н.мм:

где R – радиус блока, мм.

Угол закручивания пружины, рад:

В уравновешивающем механизме с торсионом 5 (рис. 12.19) между блоком 2 и торсионом 5 установлена повышающая зубчатая передача, целесообразность применения которой обусловлена ограничениями на угол закручивания торсиона.

Крутящий момент торсиона, Н мм:

Угол закручивания торсиона, рад:

Ò a b ,

R u

где u – передаточное отношение зубчатой передачи.

349

12.8. Системы уравновешивания силовых статических нагрузок

Силовые статические нагрузки возникают только в поступательных степенях подвижности исполнительного устройства робота.

Они постоянны и не зависят от перемещений в других степенях подвижности.

Для уравновешивания силовых статических нагрузок может быть использован пружинный механизм как с постоянной, так и с синусно-косинусной нагрузочной характеристиками.

При использовании механизмов уравновешивания с постоянной нагрузочной характеристикой необходимо учитывать, что их массогабаритные характеристики определяются в основном параметрами блок-кулачка и пружины.

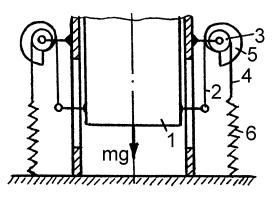
На рис. 12.20 изображена система уравновешивания вертикального перемещения звена 1 массой m исполнительного устройства робота. Она состоит из двух одинаковых уравновешивающих механизмов с постоянной нагрузочной характеристикой.

Каждый такой механизм включает в себя трос 2, одним концом Рис. 12.20 закрепленный на перемещающемся звене 1, а вторым – на кулачке пе-

ременного радиуса 5, трос 4, закрепленный одним концом на блоке 3 постоянного радиуса, а вторым концом через пружину 6 – на корпусе исполнительного устройства робота.

При опускании звена 1 трос 2 поворачивает блок-кулачок. При этом трос 4 растягивает пружину 6, что приводит к увеличению ее силы F упругой деформации, которая и создает уравновешивающий момент, равный моменту от массы m подвижного звена 1.

Для сокращения габаритов уравновешивающего механизма целесообразно пружину размещать параллельно оси поступательной степени подвижности, а блок-кулачок – перпендикулярно к оси.

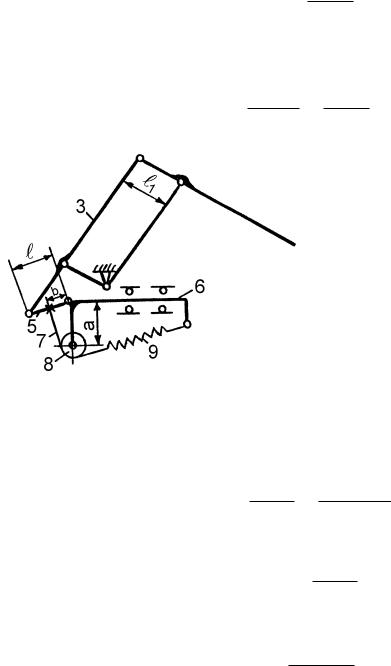
На рис. 12.21 изображена схема устройства поступательной степени подвижности исполнительного устройства робота. Она включает в себя: механизм вертикального перемещения уравновешиваемого звена 9, перемещающегося в направляющих 1; пружинную систему уравновешивания с постоянной нагрузочной характеристикой, имеющую блок-кулачок 6, который установлен на опо-

350

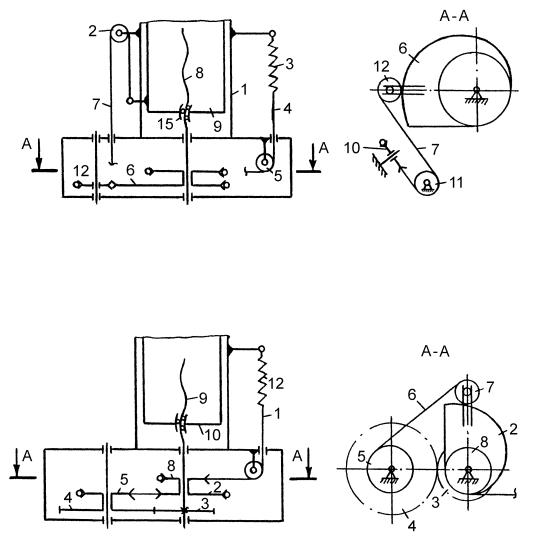
рах качения соосно приводному элементу (винту) 8, связан с одной стороны с помощью гибкого элемента 4 и ролика 5 с пружиной 3, а с другой стороны с помощью гибкого элемента 7 и роликов 2, 10, 11 и 12 с гайкой 15.

Рис. 12.21

Вращение винта 8 вызывает поступательное перемещение гайки 15 и уравновешиваемого звена 9, что приводит к повороту блоккулачка 6 и изменению деформации пружины 3.

Рис. 12.22

В отличие от предыдущей схемы механизма на рис. 12.22 изображена схема уравновешивающего механизма, у которого гибкий элемент 1, связанный с пружиной 12, закреплен на шкиве 8 постоянного радиуса, а гибкий элемент 6 одним концом закреплен на шкиве 5, также постоянного радиуса, а другим – через промежуточный шкив 7 – на кулачке 2. Ведущее звено (винт) 9 через зубчатую передачу, состоящую из зубчатых колес 3 и 4, связано со шкивом 5.

Вращение винта 9 вызывает перемещение уравновешиваемого звена 10 и одновременно поворот кулачка 2 и связанного с ним зубчатого колеса 3, которое, в свою очередь, поворачивает зубчатое колесо 4 со шкивом 5. В результате деформация пружины 12 изменяется, что приводит к изменению ее силы и уравновешиванию звена 10.

351

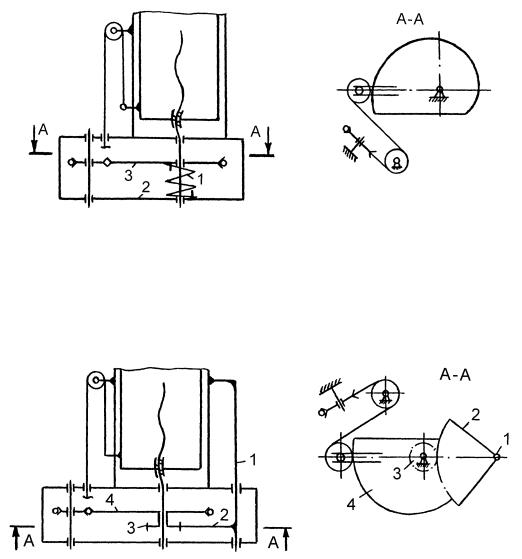
К улучшению компоновки уравновешивающего механизма подъема звена относительно небольшой массы может привести замена пружины растяжения (сжатия) на пружину 1 кручения, устанавливаемую между корпусом 2 и кулачком 3 (рис. 12.23).

Рис. 12.23

В уравновешивающих механизмах подъема звена с относительно небольшим его перемещением (рис. 12.24) возможна замена пружины растяжения (сжатия) на торсион 1, на котором установлено зубчатое колесо 2, входящее в зацепление с зубчатым колесом 3, жестко соединенным с кулачком 4.

Рис. 12.24

Рассмотрим механизм подъема звена 2 массой m, выполненный на основе шарнирного параллелограмма (рис. 12.25).

Используя принцип возможных перемещений, запишем: m g dh T d ,

где T – вращающий момент на валу 1, Н.мм; h – перемещение звена 2, мм:

h L sin ,

где L – длина рычага 3 параллелограмма, мм; – угол наклона звена 3 параллелограмма к горизонтали, град; dh – элементарное линейное перемещение звена 2, мм:

352

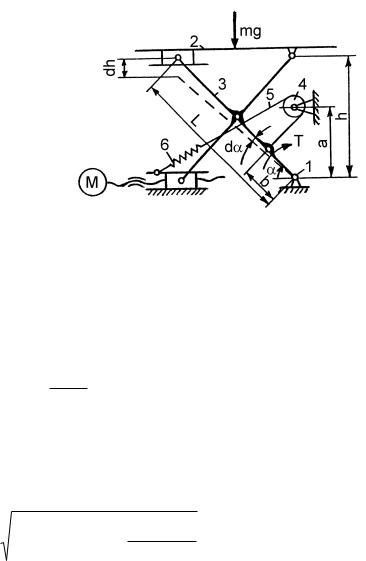
dh L cos d ;

d – элементарное угловое перемещение звена 3 параллелограмма, град.

После подстановки получим:

где a – расстояние между валом 1 и осью блока 4, мм; b – расстояние между валом 1 и точкой крепления троса 5 к звену 3 параллелограмма, мм.

Максимальная (минимальная) деформация пружины, мм:

Если параллелограмм состоит из n секций, то в приведенной формуле нужно заменить L на nL.

12.9. Системы уравновешивания моментных статических нагрузок

Моментные статические нагрузки возникают только во вращательных степенях подвижности исполнительного устройства робота.

353

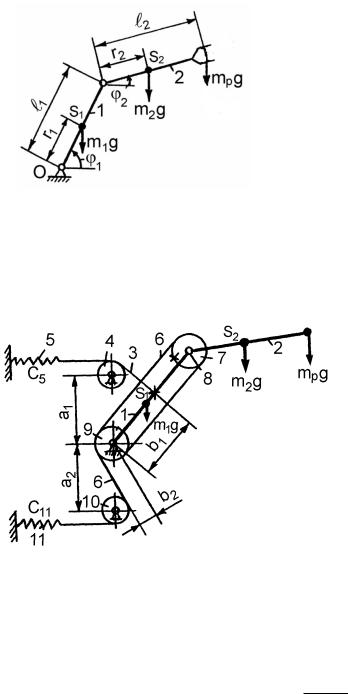
Рассмотрим исполнительное устройство робота, работающее в ангулярной (угловой) системе координат (рис. 12.26). Составим

максимальный момент на выходном валу привода звена 2 от внешних нагрузок, приложенных к этому звену, Н.мм; r1 – расстояние от первой степени подвижности до центра S1 масс

Рис. 12.26 первого звена, мм; r2 – расстояние от второй степени подвижности до цен-

тра S2 масс второго звена, мм; m1, m2 и mр – массы соответственно первого и второго звеньев и рабочего органа, кг; 1 и 2 – углы поворота первого и второго звеньев относительно горизонтали соответственно, град.

Так как моменты на валах изменяются по косинусоидальному закону, то для уравновешивания моментных статических нагрузок можно применить пружинную систему уравновешивания с си- нусно-косинусной нагрузочной характеристикой (рис. 12.27), состоящую из двух уравновешивающих механизмов.

Первый уравновешивающий механизм предназначен для компенсации момента Т1 и состоит из троса 3, прикрепленного к звену 1, блока 4 и пружины 5.

Жесткость пружины 5 равна:

c5 Ò1max .

a1b1

354

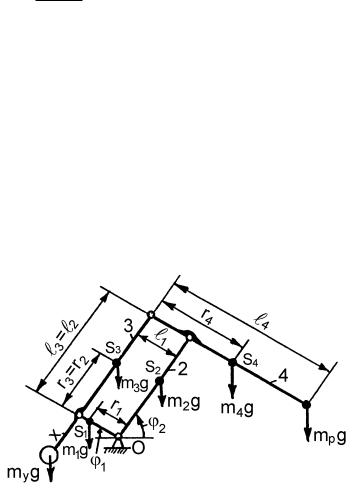
Второй уравновешивающий механизм предназначен для компенсации момента Т2 и состоит из троса 6, закрепленного на блоке 7, который жестко соединен с валом 8 звена 2, блоков 9 и 10 и пружины

11.

Жесткость пружины 11 равна:

Рассмотрим исполнительное устройство робота, выполненное в виде пантографа (рис. 12.28).

Составим уравнение моментов относительно точки О:

Моменты изменяются по косинусоидальному закону. Поэтому для уравновешивания моментных статических нагрузок можно применить пружинную систему уравновешивания с синусно-косинусной нагрузочной характеристикой аналогичную рассмотренной выше.

Данный механизм мо-

жет быть уравновешен одной постоянной массой mУ, приложенной на продолжении звена 3 (рис. 12.28). Для нахождения этой массы и точки ее приложения рассмотрим равновесие всей системы относительно точки О:

Т1 max cos 1 Т2 max cos 2 mУ g x cos 2 1 cos 1 0 ,

откуда получим:

355

Расстояние x от шарнира на звене 3 до точки приложения массы mУ, мм:

(рис. 12.28) во всем диапазоне перемещений звеньев исполнительного устройства робота.

Жесткость пружины равна:

но

12.10. Системы уравновешивания комбинированных статических нагрузок

Комбинированные статические нагрузки возникают при одновременном поступательном и вращательном движениях звена исполнительного устройства робота.

356