
Конспект лекций по КМР
.pdf
Обозначим
|
|
|
|
n |
|
|
|
|
|
|
|
|
k |
|
C |
|
|
|
|
|
|
|
m |
m r |
|
|
|
|
|
k i |
|
|
|
i |
|
|
|
|
|
|
|
|
||
K |
|
|
|
|
|
|
|
|
2i |
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
m k |
|
|
|
|
|
|
|
|
k i |
|
|
|
,
где К2i =1,1...2,0 – коэффициент конструкции.
Тогда момент сопротивления от неуравновешенности масс будет равен:
n |
k |
|
THi K 2im g k cos j , |
(8.10) |
|
k i |
j 1 |
|
где
k
- длина k-го звена, м. Если рассматриваемая система звеньев
исполнительного устройства уравновешена без объекта, то К2i=1. Эту формулу используют в проектных расчетах, когда массы
всех звеньев неизвестны. Динамический момент, Н м:
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
J |
J w |
|
|
||
|
|
|
k |
|
|
2 |
|
|
||
|
n |
|
|
ном |
|
|
||||
|
k i |
|
|
|
|
i |
|
|||
Tui |
J k J i |
|
|
|
|
|
|
, |
(8.11) |
|
|
|
|
|
|
2K |
|
|
|
|
|
k i |
|
|
|
|
|
|
||||
|
|
|
|
љi |
i |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
где Jk – момент инерции k-го звена относительно i-й степени подвижности, кг м2; J – момент инерции объекта относительно i-й степени подвижности, кг м2; i- угловое ускорение i-го звена, с-2:
|
|
|
w |
2 |
|
|
|
w |
2 |
|
|
|
|
ном |
i |
|
ном |
|
|||
|
|
|
|
|
i |
|
||||
|
|
|
|
|
|
|
|
|
||
|
i |
|
2 |
|
|
|
2K |
|
|
|
|
|
|
pi |
|
|
|
||||
|
|
|
|
|
|
|
|
љi |
i |
|
|
|
|
|
|
|
|
|
|
|
|
,
w |
íîì |
– номинальная угловая скорость i-го звена, с-1; pi – угол |
||
|
i |
|
|
|
разгона i-го звена, рад; |
i |
– полное угловое перемещение i-го зве- |
||
на, рад;
K öi
– характеристика цикла i-го привода:
|
|
|
|
|
K љi |
|
pi |
. |
|
|
||||
|
|
|
||
|
|
i |
|
Формула справедлива для готовой или спроектированной конструкции исполнительного устройства робота, когда моменты инерции всех звеньев известны.
В проектных расчетах, когда моменты инерции звеньев исполнительного устройства робота неизвестны, динамический момент находят по формуле:
|
K |
|
J w2 |
|
|
Tui |
|
3 i |
ном i |
, |
(8.12) |
|
|
|
|||
|
|
2K љi i |
|
||
190

где К3i – коэффициент конструкции:
|
|
|
|
|
n |
|
|
|
|
|
|
|
J k |
||
K |
|
|
|
1 |
k i |
|
|
3 i |
|
J |
|
||||
|
|
|
|||||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
.
В проектных расчетах принимают К3i=1,8...2,3.
Момент инерции объекта относительно i-й степени подвижности равен:
J J o mhi2 ,
где Jo – момент инерции объекта относительно центральной оси х, у или z. Для объекта в виде шара J o 0,4mR2 ; R – радиус шаровой поверхности, мм. Для других тел центральные моменты инерции приведены в специальной литературе; hi- расстояние от i-й степени подвижности до объекта по горизонтали:
i |
|
n |
k |
|
|
||
h |
|
|
|
|
|
k i |
|
k
cos j j 1
,
k
– длина k-го звена.
Следовательно, динамический момент инерции равен:
|
K |
|
J |
|
mh2 |
|
w2 |
|
|
Tui |
|
3 i |
|
o |
i |
|
ном i |
. |
(8.13) |
|
|
|
|
2K љi i |
|
||||
|
|
|
|
|
|
|
|
||
После подстановки (8.10) и (8.13) в (8.8) получим формулу проектного расчета для определения момента сопротивления i-го привода исполнительного устройства робота:
|
|
|
|
n |
|
|
k |
|
|
|
K |
|
J |
|
|
2 |
w |
2 |
|
|
|
|
|
|
|
|
|
|
3i |
o |
mh |
ном |
|
||||||
T |
K |
|
mg |
|
|
cos |
|
|
|
|
|
|
|
i |
|
i |
|||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
i |
|
2i |
|
|
|
j |
|
|
|
|
|
2K |
|
|
|
|
|||
|
|
|
|
k 1 |
|
|
j 1 |
|
|
|
|
|
|
|
i |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
љi |
|
|
|||
.
(8.14)
Подставляя (8.9) и (8.11) в (8.8), получим формулу проверочного расчета для определения момента сопротивления i-го привода исполнительного устройства робота:
|
|
|
|
|
|
|
|
|
|
|
|
n |
J |
|
|
w2 |
|
|
|
n |
|
|
|
|
k |
|
|
|
|
|
k |
J |
|||
|
|
|
|
|
|
|
|
|
|
|
|
ном i |
|||||
|
|
|
|
|
|
|
|
|
k i |
|
|
|
|
|
|||
T |
m |
m g r |
cos |
|
|
|
|
|
|
. (8.15) |
|||||||
j |
|
|
|
|
|
||||||||||||
i |
|
k |
|
Ci |
|
|
|
|
|
|
2K љi i |
||||||
|
k i |
|
|
|
|
j 1 |
|
|
|
|
|
|
|||||
191

8.9. Выбор двигателя привода
Если в качестве двигателя используют пневмоцилиндры и гидроцилиндры, то типоразмер цилиндра выбирают по усилию на штоке Føò , которое определяется силой сопротивления F или мо-
ментом сопротивления Т, необходимым для перемещения объекта в зависимости от вида движения – поступательного или вращательного:
Føò |
F или Føò |
T |
, |
|
h |
||||
|
|
|
||
где h – плечо действия силы |
Føò , м. |
|
|
По соответствующим стандартам подбирают ближайший типоразмер цилиндра. В конструкциях исполнительных устройств роботов используют стандартные пневмоцилиндры и гидроцилиндры.
Если давление в сети отличается от номинального, то определяют размер поршня, мм:
где
nу
|
4n |
F |
|
|
D |
у |
шт |
, |
|
P |
||||
|
|
|||
– коэффициент, учитывающий тип уплотнения. Для порш-
ней с манжетным уплотнением он равен 1,5; для поршней с металлическими кольцами nу =1,1...1,3; Р – давление в сети, МПа.
По найденному значению диаметра поршня выбирают из стандартов типоразмер цилиндра.
Типоразмер поршневых и шиберных поворотных двигателей, шиберных пневмомоторов и электрогидравлических шаговых приводов определяют по значению вращающего момента на выходном
валу Тk=Т.
При проектировании специальных цилиндров необходимо выполнять условие L/D 18...20, где L – длина цилиндра, мм.
Увеличение этого отношения ведет к возникновению вибраций и автоколебаний.
Отношение диаметра штока dш к диаметру поршня D выбирают конструктивно в пределах 0,2...0,7. Большие значения выбирают для более нагруженных цилиндров.
Электродвигатель выбирают по требуемой мощности, приведенной к валу двигателя, и требуемому моменту.
Для привода линейного движения требуемую мощность элек-
тродвигателя, Вт, определяют по формуле: |
|
|||
P |
F v |
, |
(8.16) |
|
|
||||
|
|
|
||
192

где F – усилие сопротивления на выходном звене привода, Н; v – линейная скорость выходного звена привода, м/с; – коэффициент полезного действия привода.
Для привода углового движения требуемую мощность электродвигателя, Вт, определяют по формулам:
P T |
w |
|
|
||
|
или
P
T n 9,55
,
(8.17)
где Т – момент сопротивления на выходном звене привода, Н м; w
– угловая скорость выходного звена привода, с-1; n – частота вращения выходного звена привода, об/мин.
Так как электродвигатели одной и той же мощности имеют разные номинальные Tном и максимальные Tд.max вращающие моменты, то необходимо определить требуемые номинальные моменты Tд.тр и требуемые максимальные моменты Tд.тр.max:
|
|
|
T |
|
|
; |
|
|
|
|
|
|
|
T |
|
|
н |
|
|
|
|
|
|
|
|||
|
д.тр |
|
u |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
T |
|
T |
|
|
T |
|
|
|
|
|
|
|
|
u |
|
|
|||||
|
|
|
|
н |
|
|
, |
||||||
T |
д.тр.max |
|
|
|
|
|
|
||||||
|
|
|
|
|
u |
|
|
u |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
(8.18)
где Tí – момент сопротивления от неуравновешенности масс звеньев и объекта, Н м; Tu – динамический момент сопротивления,
Н м; T – момент сопротивления на выходном звене привода, Н м; u – передаточное отношение привода (см. п. 8.10).
Окончательно тип электродвигателя выбирают по каталогам, исходя из условий:
|
|
Pд P; |
|
Tном Tд.тр; |
(8.19) |
|
|
Tд.max Tд.тр.max. |
|
Приводы исполнительных устройств промышленных роботов работают в повторно-кратковременном режиме. На рис. 8.5 приведена циклограмма нагружения привода. Учитывая, что время разгона и торможения привода значительно меньше времени установившегося движения, можно определить значение требуемой среднеквадратичной статической мощности, приведенной к валу двигателя, Вт:
193

|
|
n |
|
|
|
|
W |
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
P |
|
|
|
|
ном |
t 2 |
|
|
|
|
CK |
|
|
|
|
PK |
||
P |
|
K 1 |
|
|
|
WPK |
|
|||
|
|
n |
|
|
|
|
|
|
||
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
K |
tPK |
|
||
|
|
|
|
K 1 |
|
|
|
|
|
|
, |
(8.20) |
где
чем
PCK – требуемая статическая мощность двигателя на К-м рабоучастке нагрузочной циклограммы двигателя, Вт.
Рис. 8.5
Для привода поступательного движения:
PCK |
F |
v |
K |
|
HK |
|
, |
||
|
|
|||
|
|
|
||
(8.21)
где FHK – сила сопротивления от неуравновешенности масс на К-м
рабочем участке циклограммы, Н; |
vK - линейная скорость выходно- |
|||||||
го звена привода на К-м рабочем участке циклограммы, м/с. |
|
|||||||
Для привода вращательного движения: |
|
|
|
|
||||
P |
T |
wK |
|
или P |
T |
nK |
, |
(8.22) |
|
|
|||||||
CK |
HK |
CK |
HK 9,55 |
|
|
|||
где THK – момент сопротивления от неуравновешенности масс на К-м рабочем участке циклограммы, Н м; nK – частота вращения выходного звена привода на К-м рабочем участке циклограммы,
194

об/мин; wK – угловая скорость выходного звена привода на К-м
рабочем участке циклограммы, с-1; К – число включенных состояний двигателя за цикл; wíîì – номинальная скорость вращения вала двигателя, с-1; wPK - рабочая скорость вращения вала двигателя на К-м рабочем участке циклограммы, с-1; tPK – длительность К-го
рабочего участка циклограммы, с; |
w |
- коэффициент, учитываю- |
|
|
K |
щий теплоотдачу при понижении |
скорости вращения двигателя |
|
(скорости перемещения исполнительного устройства) по отношению к номинальной. Такое понижение скорости может быть вызвано условиями обеспечения требуемого технологического процесса:
|
|
|
|
|
1 |
|
|
w |
|
|
|
|
|
|
PK |
||||
|
|
|
|
|
|
|
|
|
|
|
w |
K |
|
o |
|
o |
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ном |
,
(8.23)
где o =0,7...0,78 – для двигателей закрытого исполнения. Вычисляем требуемый номинальный момент двигателя, Н м:
T |
|
|
T |
|
НКmax |
||
|
|
|
|
|
д.тр |
|
u |
|
|
|
(8.24)
и требуемый максимальный
Tд.тр.max
момент двигателя, Н м |
||||||
|
T |
|
T |
T |
|
|
Кmax |
НК |
ИК max |
||||
|
|
|||||
|
u |
|
|
u |
|
|
,
(8.25)
где TÍÊmax – максимальный момент сопротивления от неуравновешенности масс звеньев и объекта на выходном звене привода на К-м рабочем участке циклограммы, Н м, TÊmax – максимальный момент сопротивления на выходном звене привода на К-м рабочем участке циклограммы, Н м; TÈÊ – динамический момент сопро-
тивления на К-м рабочем участке циклограммы, Н м.
Тип электродвигателя выбирают по каталогам, исходя из условий:
P P ; |
|
|
|
|
|||
|
д |
|
c |
|
|
|
|
|
T |
|
|
; |
|
||
T |
ном |
д.тр |
|
||||
|
|
|
|
|
|||
|
|
|
T |
|
|
. |
|
T |
д.max |
д.тр.max |
|||||
|
|
|
|
||||
(8.26)
При выборе типа электродвигателя необходимо также учитывать его конструктивные особенности, геометрические параметры, массо-габаритные характеристики, срок службы и др.
195

8.10. Передаточное отношение привода
Передаточное отношение привода степени подвижности исполнительного устройства робота при незначительных динамических нагрузках (преобладают неуравновешенные нагрузки) может быть определено по формуле:
u |
|
д |
|
M |
Н |
|
, |
(8.27) |
||
|
|
|
|
|||||||
|
|
M |
|
|
|
|||||
|
ћ‰ |
|
д.тр |
|
|
|||||
|
|
|
|
|
|
|
|
|||
где д – номинальная скорость двигателя; – скорость выходного звена преобразователя движения; MH – нагрузка сопротивления на выходном звене преобразователя движения; M – требуемое
усилие двигателя.
В зависимости от характера движения выходных звеньев двигателя и механического преобразователя и M могут принимать
следующие значения: |
|
|
|
w – при угловом движении; |
|
|
v – при линейном движении. |
|
|
||
|
||
|
T – при угловом движении; |
|
M |
||
|
||
|
F – при линейном движении. |
Следует отметить, что передаточное отношение в общем случае имеет размерность. Так, при преобразовании вращательного движения в поступательное размерность передаточного отношения (1/м), при преобразовании поступательного движения во вращательное размерность передаточного отношения (м).
Для привода вращательной степени подвижности B (рис. 8.6) передаточное отношение находят по формуле:
u |
w |
д |
|
||
|
|
|
|
w |
|
|
T |
|
H |
|
|
|
|
|
T |
д.тр |
|
|
|
,
(8.28)
где wд – номинальная угловая скорость двигателя, c-1; w – угловая скорость выходного вала преобразователя движения, c-1; Tд.тр – требуемый вращающий момент на валу двигателя, Нм; – коэффициент полезного действия преобразователя движения привода; TH – момент сопротивления, Hм, на выходном валу степени по-
движности от неуравновешенности масс выходной системы подвижных звеньев исполнительного устройства (системы звеньев ВСД исполнительного устройства, расположенной за рассматриваемой степенью подвижности) и объекта вместе.
196

Для привода поступательной степени подвижности А (рис. 8.6) при преобразовании вращательного движения в поступательное:
|
u |
wд |
|
|
FH |
|
, |
(8.29) |
|
|
v |
Tд.тр |
|||||||
где v – линейная скорость функ- |
|||||||||
ционального |
звена |
поступатель- |
|||||||
ной |
степени |
подвижности, м/с; |
|||||||
FH |
– сила сопротивления, Н, на |
||||||||
функциональном |
звене |
степени |
|||||||
подвижности |
от |
неуравновешен- |
|||||||
ности масс выходной подвижной |
|||||||||
системы звеньев AВСД исполни- |
|||||||||
тельного |
устройства |
и |
объекта |
||||||
вместе. |
|
|
|
|
|
|
|
Рис. 8.6 |
|
|
|
|
|
|
|
|
|
|
|
|
Для |
привода |
вращательной |
||||||
степени подвижности С (рис. 8.6) при преобразовании поступательного движения во вращательное:
u |
v |
д |
|
||
|
|
|
|
w |
|
|
T |
|
|
H |
|
F |
д.тр |
|
|
|
,
(8.30)
где Fд.тр – требуемая сила на подвижном звене двигателя линейного перемещения, Н; vд – номинальная линейная скорость подвиж-
ного звена двигателя, м/с.
В том случае, когда на процесс перемещения в степени подвижности исполнительного устройства существенное влияние оказывают динамические нагрузки и не требуется получить заданную скорость перемещения выходного звена механического преобразователя, определяют оптимальное по быстродействию (время перемещения объекта по степени подвижности минимальное) передаточное отношение привода:
u 3 |
|
2 2 |
P |
|
|
|
|
д |
H |
, |
(8.31) |
||
|
|
|||||
|
q M u |
|||||
где РН – масса (момент инерции) выходной системы подвижных звеньев исполнительного устройства с объектом:
|
JH |
– при угловом движении; |
PH |
|
|
|
mH - при линейном движении; |
|
197

q – перемещение функционального звена (выходного звена механического преобразователя привода) рассматриваемой степени подвижности:
q
S
–при угловом движении;
–при линейном движении.
При эксплуатации робота перемещение функционального звена может изменяться в зависимости от технологического процесса. Поэтому при проектировании исполнительных устройств перемещение функционального звена можно приближенно принимать
равным половине его максимального перемещения, т.е. q qmax2 ;
M u – динамическая (инерционная) нагрузка, возникающая в пе-
риод разгона и торможения выходной системы подвижных звеньев исполнительного устройства и объекта:
M u
Tu Fu
–при угловом движении;
–при линейном движении.
Для привода вращательной степени подвижности B (рис. 8.6) оптимальное передаточное отношение:
u 3 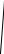
2w |
2 |
J |
|
||
д |
H |
||||
|
|
|
|||
T |
u |
|
|||
|
|
|
|
||
.
(8.32)
Эта формула справедлива только для трапецеидального закона изменения скорости w, характерного для приводов, в которых момент инерции нагрузки J H превышает собственный момент инерции двигателя:
|
J |
|
|
u |
|
H |
|
2 |
J |
|
|
|
|
|
|
|
|
|
д |
1
,
где J д – момент инерции вращающихся частей двигателя с учетом приведенного к валу двигателя момента инерции преобразователя движения степени подвижности, кг м2:
J д 1,1 1,3 J p , |
(8.33) |
J p – момент инерции ротора двигателя, кг м2, содержится в ката-
логах двигателей. Если отношение
J H |
1, |
|
u2 J д |
||
|
198

то передаточное отношение привода определяют по формуле:
u |
J |
|
J |
||
|
H д
.
(8.34)
Для привода поступательной степени подвижности А при преобразовании вращательного движения в поступательное:
2w |
2 |
m |
||
|
||||
u 3 |
д |
|
|
H |
|
|
|
||
s T |
u |
|
||
|
|
|
|
|
.
(8.35)
Для привода вращательной степени подвижности С при преобразовании поступательного движения во вращательное:
|
2v |
2 |
J |
|
|||
u 3 |
д |
H |
|||||
|
|
|
|
||||
|
|
|
|
|
|||
|
F |
u |
|
||||
|
|
|
|
|
|
||
В случае, когда масса объекта (момент инерции выходной системы подвижных звеньев) изменяется в широких пределах за время одного технологического цикла, для определения оптимального передаточного отношения используют формулу:
|
2 |
2 |
n |
|
|
P |
|
||
|
|
д Hj |
||
u |
|
|
j 1 |
|
n |
|
|
|
|
3 |
|
|
|
|
|
q j |
M u |
|
|
|
j 1 |
|
|
|
, |
(8.36) |
где
PHj
– масса (момент инерции) выходной системы подвижных
звеньев исполнительного устройства и объекта на j-м рабочем
участке технологического цикла; |
q j |
– перемещение функциональ- |
ного звена рассматриваемой степени подвижности на j-м рабочем участке технологического цикла.
Для привода вращательной степени подвижности В (рис. 8.6):
|
|
n |
|
|
|
|
|
2wд2 J Hj |
|
|
|
u 3 |
j 1 |
. |
(8.37) |
||
n |
|||||
|
|
j Tu |
|
|
|
|
|
j 1 |
|
|
|
199
