Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технологический университет "Станкин"

Предмет:

Проектирование и конструирование машин и роботов

Файл:

Конспект лекций по КМР

.pdf

Скачиваний:

435

Добавлен:

11.02.2015

Размер:

19.54 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 6513 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Т а б л и ц а 5.8

Таблица нормального закона распределения

P, %	UP	P, %	UP	P, %	UP

0,0001	-4,7534	19,00	-0,8779	84,00	0,9945
0,0010	-4,2649	20,00	-0,8416	85,00	1,0364
0,0100	-3,7190	22,00	-0,7722	86,00	1,0903
0,1000	-3,0902	24,00	-0,7063	87,00	1,1264
0,1500	-2,9677	26,00	-0,6433	88,00	1,1750
0,2000	-2,8782	28,00	-0,5828	89,00	1,2265
0,3000	-2,7478	30,00	-0,5244	90,00	1,2816
0,4000	-2,6521	32,00	-0,4677	91,00	1,3408
0,5000	-2,5758	34,00	-0,4125	92,00	1,4051
0,6000	-2,5121	36,00	-0,3585	93,00	1,4758
0,7000	-2,4573	38,00	-0,3055	94,00	1,5548
0,8000	-2,4089	40,00	-0,2533	95,00	1,6449
0,9000	-2,3656	42,00	-0,2019	96,00	1,7507
1,0000	-2,3263	44,00	-0,1510	97,00	1,8808
1,2000	-2,2571	46,00	-0,1004	98,00	2,0537
1,4000	-2,1973	48,00	-0,0502	98,20	2,0969
1,6000	-2,1444	50,00	0,0000	98,40	2,1444
1,8000	-2,0969	52,00	0,0502	98,60	2,1973
2,0000	-2,0537	54,00	0,1004	98,80	2,2571
3,0000	-1,8808	56,00	0,1510	99,00	2,3263
4,0000	-1,7507	58,00	0,2019	99,10	2,3656
5,0000	-1,6449	60,00	0,2533	99,20	2,4089
6,0000	-1,5548	62,00	0,3055	99,30	2,4573
7,0000	-1,4758	64,00	0,3585	99,40	2,5121
8,0000	-1,4051	66,00	0,4125	99,50	2,5758
9,0000	-1,3408	68,00	0,4677	99,60	2,6521
10,0000	-1,2816	70,00	0,5244	99,70	2,7478
11,0000	-1,2265	72,00	0,5828	99,80	2,8782
12,0000	-1,1750	74,00	0,6433	99,85	2,9677
13,0000	-1,1264	76,00	0,7063	99,90	3,0902
14,0000	-1,0803	78,00	0,7722	99,9900	3,7190
15,0000	-1,0364	80,00	0,8416	99,9990	4,2649
16,0000	-0,9945	81,00	0,8779	99,9999	4,7534
17,0000	-0,9542	82,00	0,9154
18,0000	-0,9154	83,00	0,9542

В формуле для определенияпри изгибе и растяжении

F ,	параметр принимает значения

(сжатии) и при кручении.

121

									Т а б л и ц а 5.9
		Значения функции F( , )

				F ,		2		при
	lg			F ,		1		при


		0,01	0,08		0,10		0,12			0,16	0,20

0,0032	-2,5	0,885	0,774		0,720		0,668			0,569	0,480
0,0100	-2,0	0,908	0,813		0,774		0,730			0,647	0,569
0,0316	-1,5	0,931	0,863		0,829		0,796			0,730	0,668
0,1000	-1,0	0,954	0,908		0,836		0,836			0,818	0,774
0,3162	-0,5	0,977	0,954		0,942		0,931			0,908	0,885
1,0000	0,0	1,000	1,000		1,000		1,000			1,000	1,000
3,1620	0,5	1,023	1,016		1,058		1,070			1,092	1,115
10,0000	1,0	1,046	1,092		1,115		1,137			1,182	1,226
31,6200	1,5	1,069	1,137		1,171		1,204			1,269	1,382
100,0000	2,0	1,092	1,182		1,226		1,269			1,353	1,430
316,2000	2,5	1,115	1,226		1,280		1,332			1,430	1,519
1000,0000	3,0	1,137	1,269		1,332		1,392			1,502	1,596
3162,0000	3,5	1,160	1,312		1,382		1,449			1,508	1,667
10000,0000	4,0	1,182	1,352		1,131		1,502			1,627	1,726

Если в уравнении (5.17)

вместо 1 подставить 1 , то по этому уравнению получится медианное значение предела выносливости детали

1Ä вок:

на множестве

	1	1
1Д	1	1
1Д		2
		2

всех пла-

	. (5.18)
	. (5.18)	Рис. 5.11
		Рис. 5.11

В ряде случаев удобнее пользоваться уравнением подобия усталостного разрушения в виде:

max U 1 10 lg UPS .

(5.19)

122

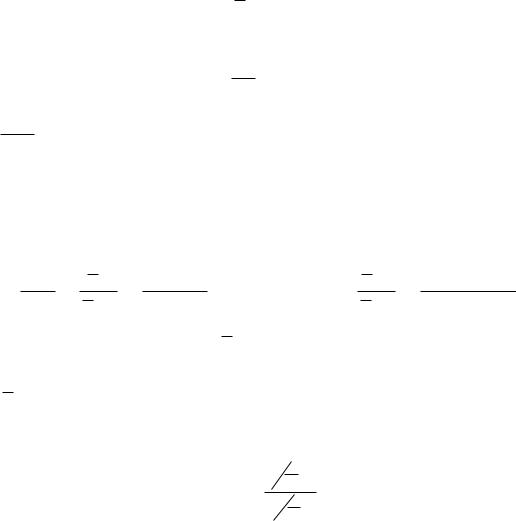
Оно получено из уравнения (5.15) заменой
	max	.
	U	.
	U

Уравнение (5.19) позволяет сразу найти значение max при за-

данном значении квантили UP, соответствующей вероятности разрушения Р.

Из уравнений (5.18) и (5.19) можно получить выражения для

определения предела выносливости детали

1Ä

, соответствую-

щего вероятности разрушения Р, для заданной плавки:

ЧS

1Д

(5.20)

lg +U

ЧS

1Д

1 10

(5.21)

– отношение, характеризующее одновременное влияние

концентрации напряжений и масштабного фактора на предел выносливости, а также отдельно эффективного коэффициента концентрации напряжений К и коэффициента влияния абсолютных

размеров

K d [20]:

;

гл

;

1Д

0,5 1 ‹гг

где

– предел выносливости гладкого образца диаметром d,

равным диаметру детали;

гл

– относительный критерий подобия

усталостного разрушения гладкого образца:

		L
			G		.
	гл	L
		L
			G	0

Для оценки функций распределения пределов выносливости

при кручении уравнения подобия усталостного разрушения аналогичны уравнениям подобия при растяжении (сжатии) и изгибе. Уравнение (5.15) при кручении имеет вид:

lg UP

S ,

(5.22)

max

1Д

где

;

1,5 ;S

S .

123

Формулы для определения G для деталей различной конфигурации приведены в табл. 5.5.

Коэффициенты вариации пределов выносливости деталей. Коэф-

фициентом вариации предела выносливости детали называют отношение среднего квадратического отклонения предела выносли-

вости	S	к среднему значению предела выносливости детали на
		1Д

множестве всех плавок данной марки

1 ä

		S
v			1Д
v			1Д
		1д
	1Д

(5.23)

При отсутствии сварки, фреттинг-коррозии, остаточных напряжений, поверхностного упрочнения и при стабильной технологии изготовления детали коэффициент вариации вычисляют по формуле [39]:

v			v2		v2
	1Д			max

	v2
1

(5.24.)

где

v max

– коэффициент вариации максимальных разрушающих

напряжений в зоне концентрации, соответствующий пределам выносливости деталей, изготовленных из металла одной плавки:

v max

		0,1
		1

(5.25)

В случае отсутствия данных в предварительных расчетах можно принимать:

v max

0,03 0,08

v 1 – коэффициент вариации средних (в пределах одной

плавки) значений пределов выносливости гладких лабораторных образцов диаметром d0=7,5 мм, учитывающий межплавочное рассеяние механических свойств металла:

где

v B

– коэффициент

v	0,04 0,10	,
1	B

вариации предела прочности металла на

множестве плавок;	v		- коэффициент вариации теоретического

коэффициента концентрации напряжений , определяемый слу-

чайными вариациями радиусов кривизны (галтелей, канавок, резьбы и т.п.) деталей в зонах концентрации напряжений. Его прини-

мают равным v		=0,02...0,10.

Коэффициент вариации пределов выносливости деталей находится в пределах v 1Ä 0,05...0,15.

124

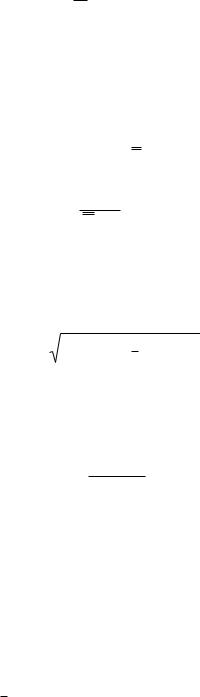
Предел выносливости детали при заданной вероятности разру-

шения определяют по формулам:
1Д		1Д 1 U P v		;	(5.26)
1Д	P	1Д 1 U P v		1Д
				.
P			1Д

5.5. Расчет на выносливость при регулярном переменном нагружении

При регулярном переменном нагружении условие прочности деталей и элементов конструкции исполнительного устройства робота основывается на статистической оценке возможных случайных отклонений амплитуды a переменных напряжений и предела вы-

носливости 1Д

детали.

Случайные отклонения амплитуды напряжений возникают вследствие нарушения режима работы и вариации нагруженности одинаковых деталей исполнительного устройства, вызванной производственными и эксплуатационными факторами.

Значения пределов выносливости также имеют значительные рассеяния вследствие неоднородности металла, различия механических свойств материалов, условий изготовления и проведения усталостных испытаний деталей.

Для линейного напряженного состояния, при изгибе или растяжении (сжатии), если пределы выносливости и амплитуды циклов распределены по нормальному закону со средними значениями

1Д	и a , вероятность разрушения Р можно получить из условия:
	U P	1 n
					,	(5.27)
		v2		v2	,	(5.27)
	n2	v2		v2
			1Д		a
			1Д		a

где UP – квантиль нормального распределения, соответствующая вероятности разрушения Р (%) (табл. 5.8); n – условный коэффициент запаса прочности по средним значениям нормальных напряжений:


	n		1Д			;
	n					;

				a
v	– коэффициент вариации амплитуд нормальных напряжений:
	a
	v		S		a	,
						,
		a	a
			a

125

– среднее значение амплитуд нормальных напряжений; S a –

среднее квадратическое отклонение амплитуды нормальных напряжений.

	При отсутствии статистических данных принимают [20]
v	=0,1...0,3.
	a
	При кручении расчет проводят аналогично.
	При совместном действии нормальных и касательных напря-

жений синхронном и однофазном их изменении квантиль нормального распределения, соответствующая вероятности разрушения

P, равна [22]:

				1			1					1
				1			n		2			n	2
									2				2

U
U	P							v		2							v	2
	P			1										1

		v2
		v2								a							a
			1Д		n	2			n		2				n	2	n		2
			1Д	1		2					2			1		2			2



					n	2									n	2
					n										n

(5.28)

			S
где	v				a
					a
		a
		a
				a

напряжений;

– коэффициент вариации амплитуд касательных

n – условный коэффициент запаса прочности по

средним значениям касательных напряжений:

1Д

5.6. Расчет на прочность при нерегулярном переменном нагружении

Нагрузки, действующие на детали исполнительного устройства робота в процессе эксплуатации, часто носят случайный характер, вследствие чего амплитуды напряжений изменяются во времени. Эти изменения могут циклически повторятся.

Учет нерегулярного характера нагруженности детали может быть осуществлен на основе использования корректированной линейной гипотезы суммирования усталостных повреждений [39], возникающих от действия амплитуд различных уровней. При этом коэффициент запаса выносливости определяют по формуле:

n	1Д	n ,	(5.29)

	экв

126

где

экв m					m
					m

	N			ai
a	N	G			1Д
P		G			1Д

			ai		n
			ai

(5.30)

– показатель наклона кривой усталости нормальных напряже-

ний в двойных логарифмических координатах [6]: m CK ;

C 5		( B в МПа),
	B
	80
	80

К – коэффициент снижения предела выносливости (см. формулу

5.8).

NG – абсцисса точки перелома кривой усталости. При отсут-

ствии

данных натурных

6	циклов;	aP
2 10

усталостных испытаний принимают [6]:

– предельное значение суммы относи-

тельных повреждений [39]:

max

0,5

1Д

при a

0,1.

0,5

1Ђ

max

Здесь aP находится в пределах 0,1...1,0. Если получим то следует принять aP =0,1;

– площадь под кривой распределения амплитуд:

<0,1,

;

i 1

max

– число

ступеней в

блоке

после

отбрасывания

ступеней

ai 0,5 1Д ,

– число

циклов повторения амплитуды ai

нор-

мальных напряжений в

блоке

после

отбрасывания

ступеней

ai 0,5 1Д ;

i – число циклов повторения амплитуды ai

в од-

ном блоке нагружения;

– число блоков нагружения за весь срок службы:

1Д

;

1Д

– максимальные амплитуды нормальных напряжений;

max

ai - амплитуды на i-м участке нагружения.

127

В расчет принимают только амплитуды, имеющие значения

0,5 1Д .

При действии нерегулярно изменяющихся во времени касательных напряжений коэффициент запаса выносливости вычисляют по аналогичной формуле:

n			1Д
n			1Д


			экв

где

(5.31)

экв‰							m	i
							m

	a	N			ai
m	a	N	G			1Д
	P		G			1Д
				ai
				ai		n
						n

(5.32)

При совместном действии нерегулярных тельных напряжений коэффициент запаса

[22]:

n	n	n	.
n			.

	n2	n2

нормальных и касавыносливости равен

(5.33)

(

Для деталей, у которых суммарное число циклов

r
i	– общее количество циклов повторения амплитуд всех
i 1

уровней в блоке нагружения), вырабатываемое за срок службы ве-

лико (

10	7	8
10		10

) вероятность разрушения Р находят из выра-

жения [22]:

			U P			1 n~				,
			U P	n~		v			v	,
				n~		v	2		v	2
				2			2			2
								1Д
								1Д
	~	n
где	~	P	– относительный коэффициент запаса; nP –
где	n	n	– относительный коэффициент запаса; nP –
		n
коэффициент нагруженности:
			n amax					;
			P		1Д
					1Д

n – коэффициент нагруженности:

n amax ;

1Д

(5.34)

предельный

128

v – коэффициент вариации амплитуд напряжений:

v	v

	a

0,1 0,3

По табл. 5.8 нормального распределения находят вероятность разрушения Р.

При действии касательных напряжений расчет проводят аналогично.

Более подробный расчет на усталостную прочность приведен в литературе [6, 20, 21, 22, 39].

129

Глава 6 РАСЧЕТ ИСПОЛНИТЕЛЬНЫХ УСТРОЙСТВ НА ЖЕСТКОСТЬ

Деформация исполнительного устройства робота состоит в основном из деформаций исполнительного механизма и преобразователей движения приводов.

На деформацию исполнительного механизма оказывают влияние длины звеньев и способ их закрепления, внешние нагрузки (массы объекта манипулирования, звеньев, приводов) и жесткость функциональных звеньев.

Деформации преобразователей движения приводов зависят от их типа, внешней нагрузки, упругой податливости элементов преобразователей движения.

При проведении расчетов на жесткость функциональных звеньев исполнительного устройства составляют его расчетную схему. Функциональные звенья представляют в виде прямолинейных стержней с сосредоточенными массами, расположенными в центре масс звеньев, и постоянной жесткости. Длины и взаимное положение стержней схемы равны реальным длинам и их реальному расположению в исполнительном устройстве. Места соединения стержней считают абсолютно жесткими. Массы приводов (двигателей и преобразователей движения) располагают на стержнях в соответствии с их реальным расположением на исполнительном устройстве. Таким образом, исполнительное устройство можно рассматривать как стержневую систему, у которой в рассматриваемый момент времени все стержни жестко соединены друг с другом.

6.1. Расчет звеньев исполнительного устройства на жесткость

Расчет на жесткость проводят с целью определения упругих деформаций, а также размеров поперечных сечений звеньев исполнительного устройства под действием внешних нагрузок. Деформации звеньев могут привести к значительной погрешности позиционирования робота.

Условие жесткости исполнительного устройства:


	Ki
	Ki

(6.1)

где Ki – линейное перемещение точки К i-го звена (угловое перемещение сечения К) под действием внешних нагрузок; Ki – допускаемое перемещение точки К i-го звена.

129

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 6513 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>