
Конспект лекций по КМР
.pdf
Кd и Кd – коэффициенты влияния абсолютных размеров поперечного сечения (масштабный фактор) [6]:
K |
d |
K |
d |
|
|
|
|
|
|
0,5 1 |
|
|
|
|
1 |
e |
2 h |
|
,
=0,01...0,03 1/мм. Меньшие значения для углеродистых сталей, средние – для легированных сталей, большие – для высокопрочных легированных сталей; h – наибольшая толщина стенки звена, мм. Для сплошного сечения h=Н/2 , где H – наибольший размер сечения. Для тонкостенных сечений значения масштабного фактора приближаются к единице.
K Kd
и
K Kd
– коэффициенты, характеризующие влияние фрет-
тинг-коррозии на предел выносливости при расчетах на усталостную прочность.
В местах напрессовки на вал или ось деталей (шестерен, шкивов, колец, подшипников, втулок и т.п.) возникает резкое снижение (в 3...6 раз) их пределов выносливости. Зарождение усталостной трещины возникает, как правило, у края напрессованной детали. Причинами такого резкого снижения предела выносливости детали является концентрация напряжений у края поверхности контакта и сложные механические и физико-химические процессы, протекающие на стыке двух сопрягаемых деталей при малых взаимных циклических проскальзываниях вследствие упругих деформаций деталей. После распрессовки на поверхности соединяемых деталей можно обнаружить следы коррозии в виде затемненных пятен, каверн, а также красный порошок, состоящий из оксидов железа (при контакте стальных деталей). Это явление называют фреттинг-коррозией или коррозией трения.
Трещины усталости в детали при фреттинг-коррозии образуются при весьма малых напряжениях (для углеродистой стали при
=30...50 МПа ).
Для вала с напрессованной деталью при передаче изгибающего момента и силы [6]:
K |
|
1 |
|
K |
|
, |
|
|
|
|
|||||
|
|
|
|||||
Kd |
|
|
|
|
|
|
|
|
1Ђ Kd 0 |
|
|||||
где
|
K |
|
|||
|
|
||||
|
|
||||
|
|
|
|
||
Kd 0 |
|||||
|
K |
|
|
||
|
|
|
|||
|
|
||||
|
|
|
|
||
Kd 0
0,38 1,48 lg d при d 150 мм;
3,6 при d 150 мм;
111

0,305 0,00139 B |
B в МПа ; |
0,65 0,014P |
при P 25Мп; |
1 |
при P 25Мп. |
Здесь d – размер детали, мм; Р – давление посадки, МПа, которое может быть подсчитано по формуле [30]:
P |
|
|
|
|
|
|
|
|
|
min |
U |
|
|
|
|
|
|
|
, |
|||
|
|
1 |
d |
|
d |
|
|
|
1 |
d |
|
d |
|
|
|
|
||||||
|
|
2 |
2 |
|
|
|
|
2 |
2 |
|
|
|||||||||||
|
d |
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
||
|
|
E |
|
d |
d |
2 |
|
1 |
|
|
E |
|
|
d |
2 |
d |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
||||||
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||
где min - наименьший табличный натяг посадки:
min
ei
ES
,
ei – нижнее предельное отклонение охватываемой детали (вала); ES – верхнее предельное отклонение охватывающей детали (отверстия – втулки). Значения ei и ES приведены в ГОСТ 25347-82, ГОСТ 25346-82 и справочной литературе; U – поправка на срезание и сглаживание шероховатости при запрессовке (если сборку выполняют нагреванием или охлаждением, U=0):
U
1,2 RZ1
RZ2
,
RZ1 и RZ2 – высоты шероховатостей посадочных поверхностей вала и втулки соответственно. Наиболее распространенные значения RZ для поверхностей прессовых посадок соединений: 10...6,3; 3,2...1,6 мкм, что соответствует 6...8 классам шероховатости; d1 – внутренний диаметр вала (если вал сплошной d1=0 ); d2 – внешний диаметр втулки; E1 и E2 – модули упругости первого рода материалов вала и втулки соответственно. Для стали Е=(2,0...2,2) 105 МПа, для чугуна Е=(1,2...1,4 ) 105 МПа, для бронзы Е=(1,0...1,1 ) 105 МПа; 1
и 2 – коэффициенты Пуассона материалов вала и втулки соответственно. Для стали =0,3, для чугуна =0,25, для бронзы =0,33.
При отсутствии передачи изгибающего момента и силы через
напрессованную деталь значение
K Kd
, подсчитанное по приведен-
ной формуле, следует умножить на коэффициент 0,85.
При кручении значение
K Kd
находят по формуле:
K |
|
K |
|
|
1 0,6 |
1 . |
|||
|
|
|||
Kd |
|
|
|
|
Kd |
|
|||
112

В табл. 5.6 приведены значения
K K d
и
K K d
для случая соеди-
нения цилиндрических деталей типа вал – втулка.
Т а б л и ц а 5.6
Значения |
K |
и |
|
K |
для звеньев в местах посадки деталей |
|
||||||||
Kd |
Kd |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Диаметр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К /Кd |
|
|
К /Кd |
|
|||
звена |
Посадка |
|
|
|
|
В, МПа |
|
|
В, МПа |
|
||||
d, мм |
|
|
|
500 |
|
700 |
900 |
1200 |
500 |
700 |
900 |
|
1200 |
|
30...50 |
S7(s6) |
|
|
2,50 |
|
3,00 |
3,50 |
4,25 |
1,90 |
2,20 |
2,50 |
|
3,00 |
|
|
K7(k6) |
|
|
1,90 |
|
2,25 |
2,60 |
3,20 |
1,55 |
1,75 |
2,00 |
|
2,30 |
|
|
H7(h6) |
|
|
1,60 |
|
1,95 |
2,30 |
2,75 |
1,40 |
1,60 |
1,80 |
|
2,10 |
|
50...100 |
S7(s6) |
|
|
3,05 |
|
3,65 |
4,30 |
5,20 |
2,25 |
2,60 |
3,10 |
|
3,60 |
|
|
K7(k6) |
|
|
2,30 |
|
2,75 |
3,20 |
3,90 |
1,90 |
2,15 |
2,50 |
|
2,80 |
|
|
H7(h6) |
|
|
2,00 |
|
2,40 |
2,80 |
3,40 |
1,60 |
1,85 |
2,10 |
|
2,40 |
|
>100 |
S7(s6) |
|
|
3,30 |
|
3,90 |
4,60 |
5,60 |
2,40 |
2,80 |
3,20 |
|
3,80 |
|
|
K7(k6) |
|
|
2,45 |
|
2,95 |
3,45 |
4,20 |
1,90 |
2,20 |
2,50 |
|
2,90 |
|
|
H7(h6) |
|
|
2,15 |
|
2,55 |
3,00 |
3,60 |
1,70 |
1,95 |
2,20 |
|
2,60 |
|
K F
и K F - коэффициенты влияния шероховатости поверхно-
сти при изгибе и кручении соответственно [6]:
K |
|
1 0,22 lg R |
|
lg |
|
|
|
F |
|
|
B |
1 , |
|||
|
Z |
|
20 |
|
|||
|
|
|
|
|
|
||
B
в
МПа
;
KF
0,575KF
0,425
,
RZ – шероховатость поверхности, Для алюминиевых сплавов:
K |
F |
1 |
|
|
|
|
|
Зависимость коэффициента |
K |
||
мкм.
0,15 lg RZ .
F шероховатости поверхности от
предела прочности В материала приведена на рис. При наличии коррозионных воздействий KF
5.7.
и
KF
следует
заменить на Kкор. – коэффициент, характеризующий снижение предела выносливости от влияния коррозии.
Коррозия при одновременном действии переменных напряжений способствует образованию и развитию усталостных трещин.
Явление постепенного накопления повреждений в металле под воздействием коррозионной среды и переменных напряжений называют коррозионной усталостью. Трещины коррозионной усталости возникают в поверхностных слоях металла. Развитие поверх-
113
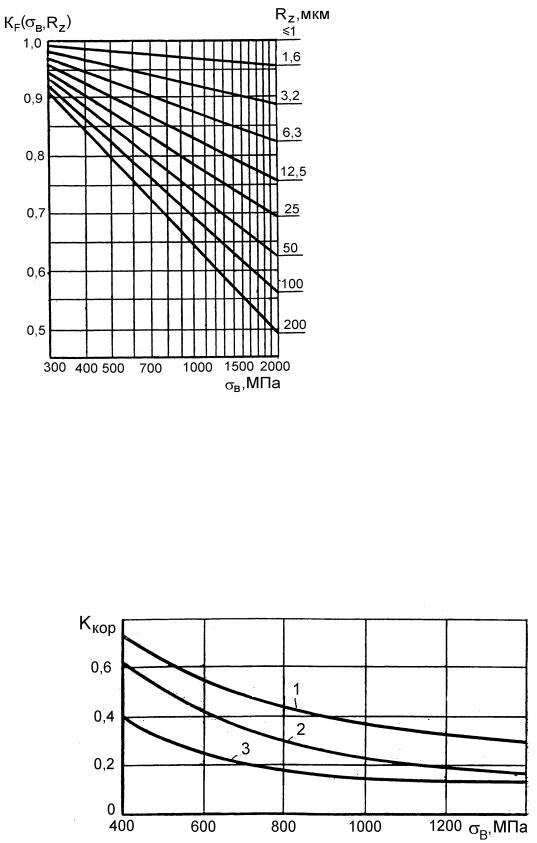
ностной коррозии зависит от свойств материала детали, коррозионной среды, времени пребывания детали в агрессивной среде, числа циклов переменных напряжений в условиях кор-
розии.
Влияние коррозии при одновременном действии коррозионной среды и переменных напряжений с частотой 30...50 Гц показаны на рис. 5.8, где 1 – для пресной воды при наличии концентрации, 2 – для пресной воды при отсутствии концентрации, 3 – для морской воды при отсутствии концентрации.
K v – коэффициент вли-
яния поверхностного упрочнения.
Поверхностное упрочнение детали можно осуществить поверхностным пластическим деформированием (обкаткой
роликами, обдувкой дробью, алмазным выглаживанием, чеканкой, раскаткой); поверхностной закалкой с нагревом током высокой частоты (ТВЧ) или лучом лазера; химико-термическими методами (цементацией, азотированием, цианированием); плазменным напылением, ионной имплантацией, поверхностным легированием).
Рис. 5.8
114

В табл. 5.7 приведены значения коэффициента ных видах поверхностного упрочнения.
Kv
при различ-
Т а б л и ц а 5.7
Коэффициент влияния поверхностного упрочнения Кv
|
Предел |
|
|
|
К v |
|
|
|
Вид поверхностной |
прочности |
Гладкие |
Звенья с концентрацией |
|||||
обработки |
сердцевины |
звенья |
|
напряжений |
|
|||
|
В, МПа |
|
|
К <1,5 |
К =1,8 |
...2,0 |
||
Закалка с нагревом |
600 |
...800 |
1,5 |
...1,7 |
1,6 |
...2,4 |
2,4... |
2,8 |
ТВЧ |
800... |
1000 |
1,2... |
1,6 |
1,6... |
2,0 |
2,0... |
2,8 |
Азотирование |
900... |
1200 |
1,1... |
1,25 |
1,3... |
2,0 |
2,0... |
3,0 |
Цементация |
900... |
1200 |
1,1... |
2,0 |
2,0... |
2,2 |
2,2... |
2,5 |
Дробеструйный наклеп |
600... |
1500 |
1,1... |
1,3 |
1,3... |
2,0 |
2,0... |
2,5 |
Обкатка роликом |
|
– |
1,1... |
1,4 |
1,4... |
1,8 |
1,8... |
2,2 |
K A
- коэффициент анизотропии [6]:
K |
|
1 |
|
B |
, |
|
|
A |
|
B |
|||||
|
|
|
|
|
|||
|
|
6000 |
|
||||
|
|
|
|
|
|||
в
МПа
.
При кручении анизотропию не учитывают.
5.4. Статистическая теория подобия усталостного разрушения
Для качественного и количественного описания влияния конструктивных факторов (концентрации напряжений, масштабного фактора, формы поперечного сечения, вида нагружения) на сопротивление усталости, была разработана статистическая теория подобия усталостного разрушения, в основе которой лежит статистическая теория прочности «наиболее слабого звена» Вейбулла.
Уравнение подобия усталостного разрушения. Его можно запи-
сать в виде [21]:
P 1 где
J |
|
|
|
max |
|
|
|||||
|
|
|
|
|
|
|
|
A |
U |
|
|
|
|
|
|
|
|
f
e |
J |
, |
|
|
|
|
|
||
x, y |
U |
m |
||
|
||||
0 |
|
|
|
|
|
|
|
||
dA A0
,
(5.9)
(5.10)
Р – вероятность появления усталостной трещины в детали при максимальном напряжении в зоне концентрации, не превышающем заданное значение max ; max f x, y – функция, характери-
115
зующая распределение напряжений по поперечному сечению; U – минимальная граница пределов выносливости, выраженных черезmax 1Д (вероятность события max <U принимается равной
нулю);
U=0,5
1
;
0
– параметр распределения Вейбулла, равный:
0
m
U |
m |
|
|
0,0152 m |
|
1
;
A0 – площадь единичного элемента (можно принять A0=1мм2); AU
– зона интегрирования, представляющая собой ту часть площади
поперечного сечения, для которой max U
метр распределения Вейбулла; |
|
0,2000 |
; m |
|
1 |
0,64 - пара- |
|
|
||||
|
|
|||
|
|
|
|
|
0,0001 B - характери- |
||||
стика механических свойств материала, определяющая его чувствительность к концентрации напряжений и масштабному фактору.
Уравнение подобия усталостного разрушения обычно записывают в виде [21]:
|
|
|
|
|
|
f x, y U |
m |
|
J |
|
|
max |
|
||||
|
0 |
|
|
|||||
|
|
|
|
|
|
|
||
|
|
A |
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dA |
P . |
(5.11) |
2,3 lg 1 |
||
A |
|
|
0 |
|
|
Рассмотрим |
пластину |
|
с двумя боковыми надрезами (рис. 5.9) при растяжении (сжатии). Линия
ABC |
изображает эпюру |
|
распределения |
напряже- |
|
ний |
max f x |
по попе- |
речному сечению (от координаты Y напряжения не зависят). В точке х=а
напряжение |
max , |
в |
|
точке |
x=a0 |
напряжение |
|
U |
. Таким образом, |
зо- |
|
ной интегрирования является отрезок a0 x a и
симметрично ему распо- Рис. 5.9 ложенный такой же отрезок слева (так как при x<a0 напряжение <U). На отрезке интегри-
рования эпюру распределения напряжений в зоне концентрации напряжений заменяют прямой линией, касательной к эпюре в точке С. Уравнение этой прямой имеет вид:
116
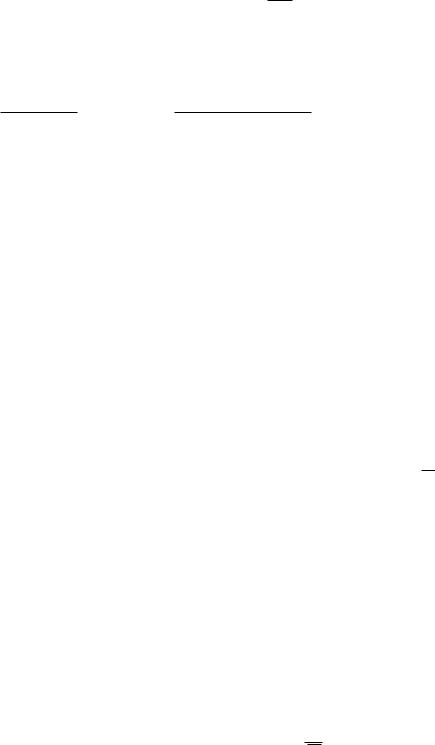
|
|
|
|
|
|
U G x a0 , |
|
|
|
||||||||
где G – градиент напряжений, МПа/мм: |
|
G |
d |
. |
|||||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
||
Откуда max f x U U G x a0 . |
|
|
dx x |
||||||||||||||
|
|
|
|
|
|||||||||||||
Тогда интеграл в уравнении (5.11) приобретет вид: |
|||||||||||||||||
|
a |
G |
x a |
|
m |
dx |
|
2 G |
m |
a a |
m 1 |
|
|||||
|
|
|
|
||||||||||||||
J 2 |
|
|
|
|
|
. |
|||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
||||
|
|
0 |
|
|
A |
|
|
|
A |
m m 1 |
|
||||||
a |
|
|
|
|
|
0 |
|
|
|
0 |
|
0 |
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При х=а и |
max |
из уравнения (5.12) получим: |
|||||||||||||||
|
|
|
|
|
|
a a0 |
|
max |
U |
. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
(5.12)
(5.13)
Подставляя это значение в выражение (5.13) и вводя обозначе-
|
|
|
|
1Д |
|
|
|
G |
|
|
ние: |
|
max |
; G |
; L 2 , |
||||||
|
U |
|
||||||||
|
|
U |
|
|
|
|
||||
|
|
|
|
|
|
|
|
max |
|
|
после преобразований получим уравнение подобия усталостного разрушения в виде:
|
|
|
L |
|
1 |
|
|
U |
m |
m 1 |
|
|
|
J |
|
|
|
|
|
|
1 |
2,3 lg 1 P , |
(5.14) |
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||
|
GA0 |
m 1 |
|
0 |
|
|
|
|
|||||
|
|
|
|
|
|||||||||
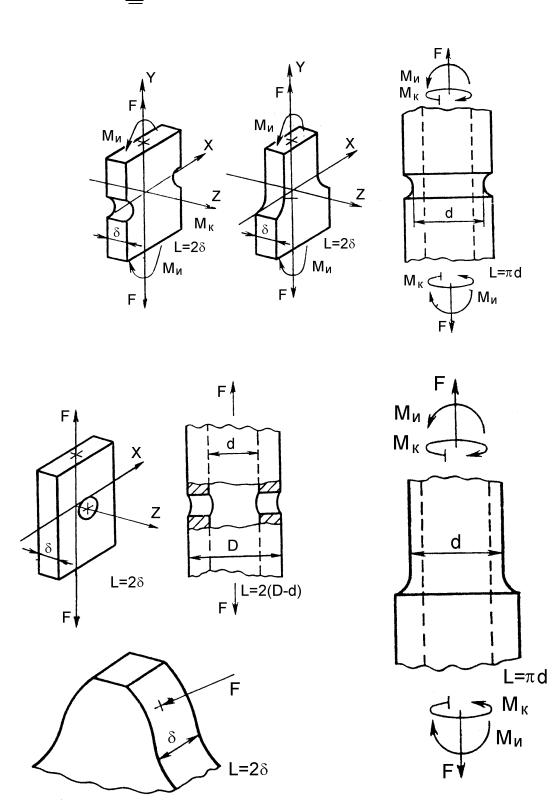
где L – периметр или часть периметра рабочего сечения детали, прилегающий к зоне повышенных напряжений, мм; формулы для
определения L для различных деталей приведены на рис. 5.10; относительный градиент первого главного напряжения в зоне центрации напряжений, 1/мм (табл. 5.5).
|
U |
m |
|
1 |
|
0,0152 m 1 . |
|
|
|
0,0152 |
0,36 |
||||
|
|
||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
G –
кон-
Это уравнение описывает семейство функций распределения величин (связь между и вероятностью Р), а, следовательно, и
пределов выносливости деталей |
|
1Д |
|
U |
различных размеров и |
|
|
|
|
|
|
|
|
|
|
|
|
очертаний при растяжении (сжатии) и изгибе. Характеристика раз-
меров и очертаний деталей дается отношением GL , называемым
критерием подобия усталостного разрушения.
Таким образом, если модель и деталь имеют различные очертания, размеры и вид нагружения, но одинаковые значения крите-
117
рия подобия
L G
, то функции распределения их пределов выносли-
вости должны совпадать.
а) |
б) |
в) |
г) |
д) |
ж)
е)
Рис. 5.10
118
Иногда
разрушения величины x
удобнее
ввиде,
lg
пользоваться уравнением подобия усталостного
соответствующего нормальному распределению |
|
1 : |
|
lg 1 lg UP S , |
(5.15) |
119

где – относительный критерий подобия усталостного разрушения:
|
L |
|
d |
|
|
|
|
G 0 |
|
2 |
|
2 |
2 |
0 |
|
|
88,3 мм |
|
L |
|
|
1 |
|
L |
|
|
|
|
G |
|
|
, |
(5.16) |
||||
L |
88,3 |
G |
|||||||
|
|
|
|
|
|||||
|
G |
0 |
|
|
|
|
|
|
– значение критерия подобия усталостного
разрушения для гладкого лабораторного образца диаметром d0=7,5 мм при изгибе с кручением.
Если образец, модель или деталь имеют разные размеры, очертания, вид нагружения, но одинаковое значение , то функции распределения их пределов выносливости совпадают.
S – среднее квадратическое отклонение случайной величины |
|||
x lg 1 , распределенной по нормальному закону [20]: |
|||
S |
0,62 |
, |
|
m 1 |
|||
|
|
||
UP – квантиль нормального распределения, соответствующая вероятности разрушения Р, % (табл. 5.8). Квантиль находится в пределах UP=0...1,0.
При UP=0 среднее значение величины x lg 1 равно: x lg 50 1 lg ,
где 50 является значением , соответствующим вероятности разрушения Р=50%. Из полученного уравнения можно найти:
|
|
|
|
1Д |
|
||
|
|
|
|
|
|||
50 |
0,5 |
|
|||||
|
|
||||||
|
|
|
|||||
|
|
|
|
|
|
1 |
|
1 |
|
|
|
.
Откуда
где 1Д |
– медианное |
|
|
|
1 |
|
|
|
|
1Д |
|
1 |
|
|
|
|
|
|
2 |
|
|
, |
(5.17) |
||
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значение для данной плавки (соответствую-
щее вероятности разрушения Р=50%) значение
1Д
; 1 – меди-
анное для данной плавки значение предела выносливости 1 . Значения функций:
F , |
2 |
|
|
|
|
||
1 |
|
||
|
|||
|
|
приведены в табл. 5.9 и на рис. 5.11.
120
