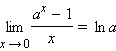Определения

Пусть имеется множество , на котором введено отношение порядка.

Последовательность элементов множества называется неубывающей, если каждый элемент этой последовательности не превосходит следующего за ним.

 — неубывающая 

Последовательность элементов множества называется невозрастающей, если каждый следующий элемент этой последовательности не превосходит предыдущего.

 — невозрастающая 

Последовательность элементов множества называется возрастающей, если каждый следующий элемент этой последовательности превышает предыдущий.

 — возрастающая 

Последовательность элементов множества называется убывающей, если каждый элемент этой последовательности превышает следующий за ним.

 — убывающая 

Последовательность называется монотонной, если она является неубывающей, либо невозрастающей.

Последовательность называется строго монотонной, если она является возрастающей, либо убывающей.

Очевидно, что строго монотонная последовательность является монотонной.

Иногда используется вариант терминологии, в котором термин «возрастающая последовательность» рассматривается в качестве синонима термина «неубывающая последовательность», а термин «убывающая последовательность» — в качестве синонима термина «невозрастающая последовательность». В таком случае возрастающие и убывающие последовательности из вышеприведённого определения называются «строго возрастающими» и «строго убывающими», соответственно.

№28. Теорема Вейерштрасса. Всякая монотонная и ограниченная последовательность имеет предел (эта теорема даётся в средней школе без доказательства). 

Основные свойства пределов.  Нижеприведенные свойства пределов справедливы не только для числовых последовательностей, но и для функций.

Если { u_n } и { v_n }   две сходящиеся последовательности, то:

Если члены последовательностей { u_n }, { v_n }, { w_n } удовлетворяют неравенствам 

№29. Число е, натуральный логарифм.

e — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число eназывают числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».

Максимум функции достигается при .

Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделахматематики.

Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718281828. Натуральный логарифм обычно обозначают как ln(x), log_e(x) или иногда просто log(x), если основание e подразумевается.

№30. Предельная точка последовательности — это точка, в любой окрестности которой содержится бесконечно много элементов этой последовательности.^[1]

 — предельная точка последовательности 

Наибольшая предельная точка последовательности называется её верхним пределом, а наименьшая предельная точка — нижним пределом.

Иногда в множество возможных предельных точек включают «» и «». Так если из последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой отрицательны, то говорят, что «» является предельной точкой этой последовательности. Если же из последовательности можно выделить бесконечно большую подпоследовательность с исключительно положительными элементами, то говорят, что «» является её предельной точкой.^[1] При этом, разумеется, у последовательности могут быть и другие предельные точки.

№31. Предел функции.

Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Число L называется пределом функции  y = f ( x ) при  x, стремящемся к  a :

если для любого  > 0 найдётся такое положительное число  = ( ), зависящее от  , что из условия | x  a | < следует  |  f ( x ) – L | < 

Это определение означает, что L есть предел функции  y = f ( x ), если значение функции неограниченно приближается к  L , когда значение аргумента  x приближается к  a. Геометрически это значит, что для любого   > 0  можно найти такое число  , что еслиx  находится в интервале ( aa ), то значение функции лежит в интервале ( L ,  L + ). Отметим, что в соответствии с этим определением аргумент функции лишьприближается  к  a , не принимая этого значения! Это следует учитывать при вычислении предела любой функции в точке её разрыва, где функция не существует.

№32. Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).

Пусть переменная  x  стремится к  a, оставаясь больше  a, и при этом  . Тогда числоA  называют правосторонним пределом (или пределом справа) функции  и обозначают любым из символических выражений

Понятие левостороннего предела (или предела слева) вводится аналогичным образом. В этом случае  приx → a  со стороны меньших значений:

Для существования обычного (двустороннего) предела функции  в точкеa  необходимо и достаточно равенство между собой односторонних пределов:

Например, в точке  x = 3  односторонние пределы функции

отличаются друг от друга:

 

Поэтому в рассматриваемой точке предел функции  не существует.

№33.  Предел в бесконечности      Число А называется пределом функции f(x) при x → + ∞ , если для каждого ε > 0 существует такое δ > 0, что всех x > δвыполняется неравенство | f (x) – A | < ε. И это записывается как

                                       

      Аналогично формулируется определение предела при x, стремящемся к минус бесконечности: число А называетсяпределом функции f(x) при x → - ∞ , если для каждого ε > 0 существует такое δ > 0, что всех x < - δ выполняется неравенство | f (x) – A | < ε.        Число А называется пределом функции f(x) при x → ∞ , если для каждого ε > 0 существует такое δ > 0, что всех  | x | > δ выполняется неравенство | f (x) – A | < ε.     При решение некоторых пределов полезно обращаться к так называемым замечательным пределам:                                          Из замечательных пределов и свойств обратной функции вытекают следующие важные пределы (при a > 0, a ≠ 1):