§6. Плоское криволинейное движение.

До сих пор мы молчаливо предполагали, что во время движения орты постоянны и дифференцировать их по времени нет необходимости. Это предположение справедливо не всегда. Например. Оно не справедливо, если происходит криволинейноедвижение. Простейший случай такого движения – движение по окружности или, в более общем случае – поплоскойкривой. Кривая называется плоской, если все её точки лежат в одной плоскости (см. рис. 1). Как легко заметить, орты координат при этом изменяют своё направление, то есть зависят от времени.

В случае вращения по окружности с постоянной по модулю скоростью известно, что на материальную точку действует центростремительнаясила

,

где – масса материальной точки,– модуль её скорости,– радиус окружности,– радиус-вектор, проведенный из центра окружности в ту точку, где в данный момент находится материальная точка. Знак минус указывает, что действующая на материальную точку сила направлена к центру окружности.

При движении по плоской кривой формулу для центростремительной силы можно обобщить. Для этого надо сделать несколько шагов.

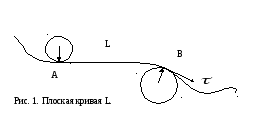
Выделим на плоской кривой Lпроизвольные точкиAиB. Построим окружности, касающиеся этих точек; стрелки указывают радиусыи, проведенные из центров окружностей в точки касания. Соответствующие радиусы (не векторы) называютсярадиусамикривизныв точкахи. Обратная величина, например,, называетсякривизнойкривойLв точке. Кривая должно быть плавной. В точке излома (в физике таких кривых не бывает) кривизна не определена. Для прямой линии кривизна стремится к нулю (радиус кривизны бесконечен). В точкекривизна считается положительной, в точке– отрицательной.

Если точка движется со скоростями и, то на неё действуют центростремительные силы, определяемые указанной формулой. Это, в частности, означает, что они движутся с центростремительным ускорением

или.

Но это не полное ускорение материальной точки. Для того, чтобы найти полное ускорение учтем, что при движении по плоской кривой скорость имеет вид

,

где – вектор, касательный к рассматриваемой точке (например, к точке В , см. рис. 1), причем он зависит от времени,- модуль скорости в этой точке.

Чтобы найти ускорение надо продифференцировать скорость:

.

Первое слагаемое называется тангенциальным (касательным) ускорением,

,

и учитывает поворот касательного орта (для движения по прямой тангенциальное ускорение равно нулю), второе слагаемое – центростремительное ускорение,

,

и учитывает изменение модуля скорости.

Таким образом, полное ускорение равно

,

а так как радиус, проведенный в точку касания перпендикулярен касательной, модуль полного ускорения равен

.

§7. Закон сохранения импульса.

В §3 мы ввели понятие импульса материальной точки как величины, равной . Импульс – аддитивная величина, то есть импульс системы материальных точек есть геометрическая сумма всехимпульсов системы:

.

Продифференцируем эту сумму по времени и учтем, что производная импульса есть сила:

.

Здесь и– силы, действующие со стороны второй и третьей материальной точки на первую точку,иа – силы, действующие со стороны первой точки на вторую и третью. Вследствие Третьего закона Ньютона они попарно сокращаются. Также попарно сокращаются все внутренние силы, действующие в систем е материальных точек. Остается только– результирующая или равнодействующая сил, действующих на систему материальных точек извне:

.

Если же система замкнута, то равна нулю и тогда после интегрирования производной полного импульса, находим

.

Это есть математическая формулировка закона сохранения полного импульса замкнутой системы материальных точек. «Полный импульс замкнутой системы материальных точек не зависит от времени, то есть сохраняется».

Задачи, для решения которых применяется закон сохранения полного импульса, достаточно известны. В частности ранее утверждалось, что если на корме небольшой лодки поставить вентилятор, который будет дуть в парус, то лодка останется неподвижной. Это не всегда так и опыты подтверждают это. Так, если не весь поток воздуха будет попадать на парус, то часть импульса проходящего мимо паруса не будет компенсировать силу отдачи и лодка начнет двигаться кормой вперед. Похожий эффект возникает, если молекулы воздуха упруго отражаются от паруса. Тогда импульсы и силы перераспределяются в пространстве, что создает отличную от нуля внешнюю силу. Картина в целом напоминает случаи рассеяния света на поглощающей и отражающей поверхностях.