§17. Момент силы, момент импульса. Уравнения моментов.

Кроме момента инерции для динамики твердого тела важны момент силы и момент импульса. Если сопоставлять движение твердого тела и движение материальной точки эти моменты являются близкими аналогами силы и импульса.

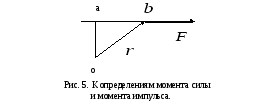
По определению, моментом силы относительно неподвижной точки о является векторная величина – векторное произведение радиус-вектора, проведенного из рассматриваемой точки о в точку приложения силы b, на вектор силы, т.е.. Аналогичным образом определяется момент импульса,. Рисунок 5 поясняет эти определения на примере момента силы. Там же указана «линия действия силы»abи «плечо силы»oa.

При определении момента импульса сила на рисунке 5 заменяется вектором импульса.

Вычислить векторное произведение можно двумя эквивалентными способами.

Первый способ связан с использованием определителей:

.

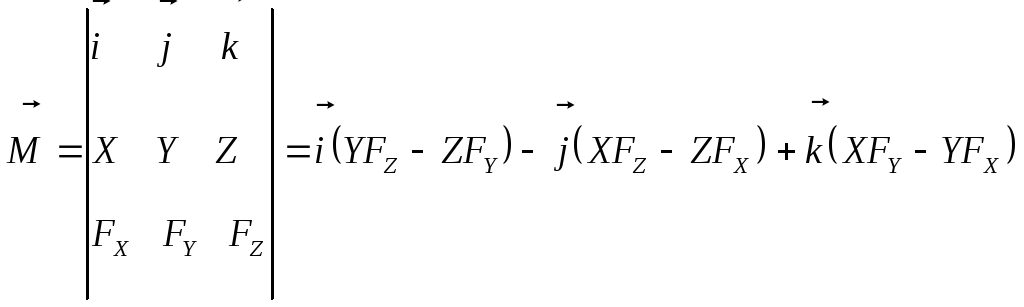Сомножители, стоящие при единичных векторах, называются проекциями моментов на соответствующие оси. Они определяют момент силы и момент импульса относительно неподвижной оси. Моменты относительно неподвижных осей – скалярные величины.

Второй способ использует представление модуля векторного произведения в виде формулы

,

где – угол между векторамии, а направление векторного произведения определяется единичным вектором, который задается движением правого буравчика, «ручка» которого привязана к радиус вектору, который поворачивается по кратчайшему расстоянию к вектору силы (буравчик перпендикулярен плоскости, в которой лежат перемножаемые векторы),

Продифференцируем момент импульса по времени. Получим

Первое слагаемое обращается в нуль, поскольку векторно перемножаются два параллельных вектора и. Учтено также, что.

Соотношение

называется уравнением моментов. При изучении движения твердого тела оно имеет такое же значение, как и Второй закон Ньютона для изучения поступательного движения материальной точки. Уравнение моментов можно назвать также уравнением вращения твердого тела.

После небольших преобразований уравнение моментов относительно неподвижной оси можно записать в виде

.

Это основной закон динамики вращательного движения твердого тела вокруг неподвижной оси. Момент инерции твердого тела, угловая скорость его вращения и результирующая моментов внешних сил, действующих на тело, рассматриваются относительно той же неподвижной оси вращения.

Если учесть теорему о движении центра масс, и потребовать, чтобы и, то можно убедиться, что два последних условия означают, что центр масс твердого тела будет двигаться прямолинейно и равномерно (или покоиться), а само тело будет равномерно вращаться вокруг оси, проходящей через центр масс (или вообще не будет вращаться). Другими словами, при выполнении указанных условий тело будет находиться в равновесии.