Вопрос 16 Интерференция двух монохроматических волн

Рассмотрим идеализированный случай сложения двух монохроматических волн одинаковой частоты. Уравнение плоской монохроматической волны, распространяющейся в положительном направлении оси X, имеет вид:

.

Если амплитуда  и начальная фаза  одинаковы во все моменты времени во всем пространстве, то волна называется однородной. Строго монохроматические волны никогда не могут быть точно реализованы в действительности и представляют идеализацию реальных волновых процессов. Условия применимости этой идеализации в каждой конкретной задаче требуют специального рассмотрения.

П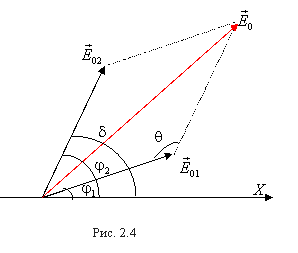усть две плоские монохроматические волны одной частоты, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления: и , где , .

Для сложения колебаний воспользуемся методом векторной диаграммы. Как видно из рис. 2.4, согласно теореме косинусов амплитуда результирующего колебания будет равна

.

Так как угол , то амплитуда результирующего колебания в данной точке определится выражением: , а интенсивность:

,

(2.4)

где  .

Если , , то интенсивность максимальна: , если , то интенсивность минимальна: .

Таким образом, при наложении двух монохроматических волн происходит устойчивое во времени перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. В тех точках пространства, для которых , результирующая интенсивность ; в точках, где , результирующая интенсивность .

Особенно отчетливо проявляется интерференция в том случае, когда интенсивности обеих интерферирующих волн одинаковы: . Тогда в максимумах , в минимумах же . Для некогерентных волн при том же условии получается всюду одинаковая интенсивность .

Ширина интерференционных полос.

Обычно экран для наблюдения интерференционной картины располагают так, чтобы оба луча и нормаль к экрану находились в одной плоскости. В этом случае ширина интерференционных полос полностью определяется углами падения световых волн на экран и длиной световой волны и не зависит от оптической схемы формирования интерферирующих волн.

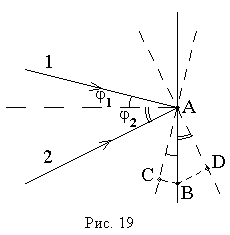Пусть две плоские световые волны падают на экран под углами  и  (рис. 19), точки  и  - середины двух соседних светлых полос на экране,  - поверхность равной фазы первой волны,  - поверхность равной фазы второй волны. Поверхность  имеет ту же фазу, что и поверхность , так как в точке  фазы двух волн одинаковые (светлая полоса). Поэтому можно считать, что это одна и та же поверхность равной фазы волны, идущей от одного точечного источника разными путями. Следовательно, оптическую разность хода, например для точки экрана , можно отсчитывать от пары точек  и  как бы общей поверхности равной фазы.

Из рис. 19 видно, что поверхность равной фазы  первой волны еще не дошла до точки  на отрезок , а поверхность  второй волны уже зашла за точку  на отрезок . Тогда оптическая разность хода  для точки  равна

.

Точки  и  - середины соседних светлых полос, тогда оптическая разность хода равна длине волны , так как при переходе по экрану на одну полосу разность хода меняется на . Выражая из этого равенства ширину полосы , и обозначая ее через , получаем

,

где знак '+' соответствует положительным углам падения  и  отсчитанным в разные стороны от нормали к экрану, как на рис. 19.

В большинстве задач углы падения малы, тогда  и выражение для ширины полос упрощается

,

где  - угол между лучами сходящимися на экране.

Эта формула сводит оптическую задачу к геометрической. Для определения ширины интерференционных полос нужно построить два луча, выходящие из одной точки источника света и попадающие в одну точку экрана. Ширина полос - это отношение длины волны света к углу между лучами, сходящимися в одну точку.

Если ширины соседних полос заметно различаются, то термина "ширина полос" избегают. Такая ситуация возникает при интерференции плоской и сферической волн, например при наблюдении колец Ньютона. Кольца Ньютона наблюдаются при интерференции волны, отраженной от сферической поверхности выпуклой линзы, и волны, отраженной от плоской поверхности, соприкасающейся со сферической поверхностью линзы. В этой задаче вместо ширины полос ищут радиус светлого (или темного) кольца с произвольным номером .