Вопрос 11

Независимые волны, которые в процессе своего распространения одновременно проходят через одну и ту же точку среды, складываются, но друг друга на искажают. Перекрещивающиеся волны, разойдясь, не несут на себе никаких следов наложения.

Подчеркните, что принцип суперпозиции точно справедлив лишь для волн бесконечно малой амплитуды.

Монохроматическая световая волна описывается уравнением гармонических колебаний:

где       y – величины напряжённостей   и , векторы которых колеблются во взаимоперпендикулярных плоскостях.

Если имеются две волны одинаковой частоты:

и                                             ;

приходящие в одну точку, то результирующее поле равно их сумме (в общем случае – геометрической):

где                                    

Если ω₁ = ω₂ и (φ₀₁ – φ₀₂) = const, волны называются когерентными.

Вопрос 12

Результат сложения волн, когда в одних местах они усиливают друг друга, а в других ослабляют, называется интерференцией (наложением).

Этот термин в 1801 году предложил английский учёный Юнг. В буквальном переводе он означает вмешательство, столкновение, встреча.

Для наблюдения интерференции необходимы условия её возникновения, их два:

1)       интерференция возникает лишь тогда, когда налагающие волны имеют одинаковую длину λ (частоту ν);

2)       неизменность (постоянство) разности фаз колебаний.

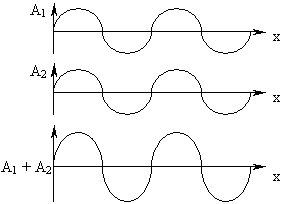
Примеры сложения волн:

Одинаковая фаза – усиление амплитуды.

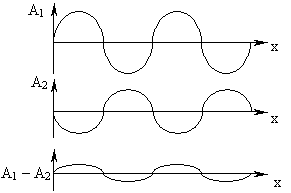
В противофазе – ослабление амплитуды.

Источники, обеспечивающие явление интерференции, называются когерентными, а волны – когерентными волнами.

Для выяснения вопроса о том, что будет в данной точке max или min, нужно знать в каких фазах волны встретятся, а для знания фаз необходимо знать разность хода волн. Что это такое?

Пусть требуется определить результат сложения в точке M, находящийся на расстояниях от источника S1 – на r1 и от источника S2 – на r2. (r2 – r1) – разность хода волн. Отсюда вывод: если источники колебались в одинаковых фазах, то:

1)        при (r₂ – r₁) = Δr, равной целому числу длин волн или четному числу полуволн, в точке М будет усиление колебаний;

2)        при d, равной нечетному числу полуволн в точке М будет ослабление колебаний.

Условие max

 

Условие min

Сложение световых волн происходит аналогично.

Сложение электромагнитных волн одной частоты колебаний, идущих от различных источников света, называется интерференцией света.

Вопрос 13

Условия наблюдения интерференций[править | править исходный текст]

Рассмотрим несколько характерных случаев:

1. Ортогональность поляризаций волн.

При этом   и  . Интерференционные полосы отсутствуют, а контраст равен 0. Далее, без потери общности, можно положить, что поляризации волн одинаковы.

2. В случае равенства частот волн  и контраст полос не зависит от времени экспозиции .

3. В случае   значение функции    и интерференционная картина не наблюдается. Контраст полос, как и в случае ортогональных поляризаций, равен 0

4. В случае   контраст полос существенным образом зависит от разности частот и времени экспозиции.

Общий случай интерференции[править | править исходный текст]

При взятии интеграла в соотношении [1] полагалось, что разность фаз  не зависит от времени. Реальные же источники света излучают с постоянной фазой лишь в течение некоторого характерного времени, называемого временем когерентности. По этой причине, при рассмотрении вопросов интерференции оперируют понятием когерентности волн. Волны называют когерентными, если разность фаз этих волн не зависит от времени. В общем случае говорят, что волны частично когерентны. При этом поскольку существует некоторая зависимость  от времени, интерференционная картина изменяется во времени, что приводит к ухудшению контраста либо к исчезновению полос вовсе. При этом в рассмотрении задачи интерференции, вообще говоря и не монохроматического (полихроматического) излучения, вводят понятие комплексной степени когерентности . Интерференционное соотношение принимает вид

Оно называется общим законом интерференции стационарных оптических полей.

Когерентность

Источники света одинаковой частоты колебаний, у которых разность фаз не зависит от времени и которые, таким образом, дают устойчивую во времени интерференцию света.

Величина А в зависимости от разности фаз лежит в пределах:

|А₁ – А₂| ≤ А ≤ (А₁ + А₂)

(0 ≤ А ≤ 2А, если А₁ =А₂)

Если А₁ = А₂, (φ₀₁ – φ₀₂) = π или (2k + 1)π, cos(φ₀₁ – φ₀₂) = –1, то А = 0, т.е. интерферирующие волны полностью гасят друг друга (min освещённости, если учесть, что Е²  J, где J – интенсивность).

Если А₁ = А₂, (φ₀₁ – φ₀₂) = 0 или 2kπ, то А² = 4А², т.е. интерферирующие волны усиливают друг друга (имеет место max освещённости).

Если (φ₀₁ – φ₀₂) – изменяется хаотически со временем, с очень большой частотой, то А₁ = 2А₁, т.е. равна просто алгебраической сумме обоих амплитуд волн, излучаемых каждым источником. В этом случае положения max и min быстро меняют своё положение в пространстве, и мы будем видеть некоторую среднюю освещённость с интенсивностью 2А₁. Эти источники – некогерентные.

Любые два независимых источника света – некогерентны.

Когерентные волны можно получить от одного источника, путём разбиения пучка света на несколько пучков, имеющих постоянную разность фаз.