Задача №3

Автомобиль массой m=2000кг движется прямолинейно со скоростью υ₀=72км/ч. В момент времени t=0 на него начинает действовать тормозящая сила, линейно растущая со временем согласно формуле , где. Определите времяt₁, необходимое для полной остановки автомобиля, и соответствующий тормозной путь S₁.

Решение

Это прямая задача механики, где по заданной силе необходимо определить движение тела.

1. При t>0 на автомобиль действует единственная горизонтальная сила , направленная против вектора скорости автомобиля. Векторное уравнение движения автомобиля в горизонтальной плоскости запишется следующим образом:

.

(1.3.1)

2. Перейдем к скалярной форме записи с помощью проекции уравнения (1.3.1) на направление вектора скорости :

.

(1.3.2)

Это обыкновенное дифференциальное уравнение первого порядка по времени относительно неизвестной функции υ.

3. Дифференциальное уравнение (1.3.2) решается методом разделения переменных υ и t:

.

(1.3.3)

Проинтегрируем левую часть по скорости от её начального значения υ₀ до текущей величины υ(t), а правую часть по времени от начального момента t=0 до текущего момента времени t

.

(1.3.4)

Выполняя интегрирование, получим

(1.3.5)

или

.

(1.3.6)

4. В момент остановки автомобиля t=t₁

,

(1.3.7)

поэтому из (1.3.6) находим, что

.

(1.3.8)

5. Тормозной путь S₁ находится с помощью определения величины скорости для прямолинейного движения:

,	(1.3.9)
,	(1.3.10)
	(1.3.11)

Ответ: t₁=8,94с; S₁=119м.

2. Гармонические колебания. Кинематика гармонических колебаний. Свободные незатухающие колебания

Рассмотрим одномерное движение частицы массой m вдоль оси х под действием консервативной силы:

,

(2.0.1)

где U(x) – потенциальная энергия частицы.

Согласно II-ому закону Ньютона уравнение движения частицы имеет вид:

.

(2.0.2)

Нас интересуют возможные положения равновесия частицы, где скорость, ускорение и действующая на частицу сила равны нулю:

(2.0.3)

Согласно (2.0.2) в положении равновесия производная потенциальной энергии по координате обращается в ноль,

,

(3.0.4)

поэтому потенциальная энергия в этих точках имеет экстремум и принимает либо максимальное, либо минимальное значение (точки перегиба здесь не рассматривается). Максимум потенциальной энергии соответствуетнеустойчивому положению равновесия, поскольку при сколь угодно малом отклонении частицы от данного положения равновесия частица под действием силы будет удаляться от исходного положения. В точке минимума потенциальной энергии имеет местоустойчивое положение равновесия. В этом случае частица, выведенная из положения равновесия внешним воздействием, стремится вернуться в исходное положение под действием возвращающей силы. При любом смещении частицы из положения устойчивого равновесия возвращающая сила всегда направлена к точке равновесия.

Наше рассмотрение ограничено важным частным случаем движения частицы в малой окрестности устойчивого положения равновесия в точке х=0, когда потенциальная энергия описывается формулой:

.

(2.0.6)

Здесь k>0 – постоянная величина.

Для этого случая уравнение движения частицы записывается следующим образом:

,

(2.0.7)

или

.

(2.0.8)

Перенесем член -kx в левую часть равенства с изменением знака и получим следующее уравнение:

.

(2.0.9)

Разделим левую и правую части полученного уравнения на массу m

,

(2.0.10)

и введем обозначение . В результате приходим к дифференциальному уравнению вида

.

(2.0.11)

Данное обыкновенное дифференциальное уравнение второго порядка по времени описывает механическую систему, которая называется гармоническим осциллятором. Примером гармонического осциллятора может служить шарик, подвешенный на вертикальной пружине.

Общее решение полученного дифференциального уравнения может быть записано в виде:

,

(2.0.12)

где – амплитуда гармонических колебаний, – круговая, или циклическая частота колебаний, связанная с частотой колебаний. Аргумент косинуса называется фазой колебаний, а постоянная- начальной фазой. При подстановке функции (2.0.12) в дифференциальное уравнение (2.0.11) это уравнение превращается в числовое тождестводля всех моментов времени.

Неизвестные величины А и находятся с помощью двух начальных условий, определяющих начальное состояние частицы и обычно задаваемых для момента времени t=0,

, .

(2.0.13)

Из начальных условий (3.0.13) следует, что

, .

(2.0.14)

Число начальных условий должно равняться числу неизвестных постоянных в общем решении обыкновенного дифференциального уравнения. В свою очередь число произвольных постоянных в общем решении обыкновенного дифференциального уравнения равно порядку этого уравнения, который определяется высшей производной искомой функции по времени.

Приведённое выше решение уравнения гармонического осциллятора описывает свободные незатухающие колебания. Смещение x, скорость V и ускорение a данных колебаний определяются формулами:

,	(2.0.15)
,	(2.0.16)
.	(2.0.17)

В случае свободных незатухающих гармонических колебаний полная механическая энергия осциллятора Е сохраняется постоянной. Она равна сумме его кинетической

(2.0.18)

и потенциальной

(2.0.19)

энергий. С учетом (2.0.12) выражение для полной энергии принимает вид:

.

(2.0.20)

Здесь использовано соотношение .
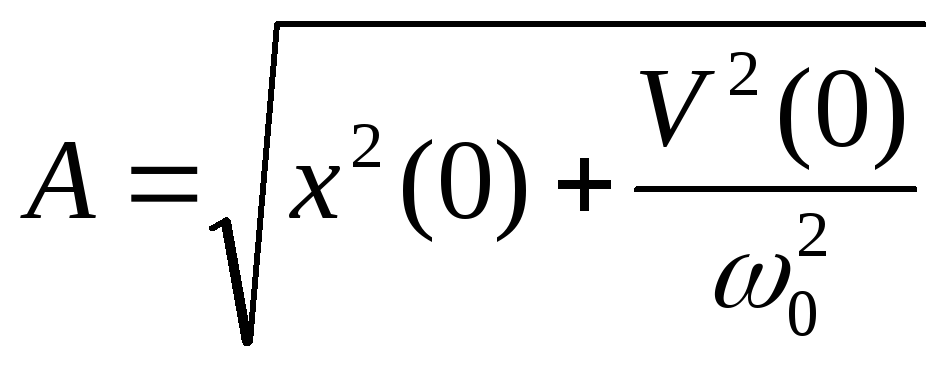
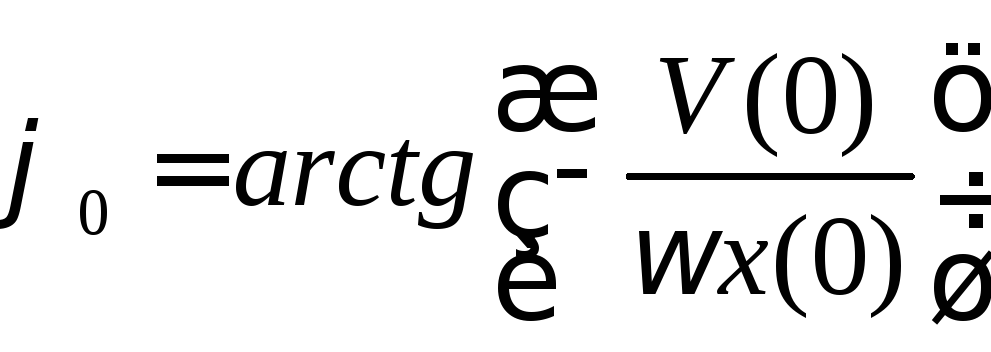