
- •А.А. Колоколов «Механика и молекулярная физика»
- •1. Динамика материальной точки
- •Задача № 1
- •Решение
- •Задача №2
- •Решение
- •Задача №3
- •Решение
- •2. Гармонические колебания. Кинематика гармонических колебаний. Свободные незатухающие колебания
- •Задача №4
- •Решение
- •Задача №5
- •Решение
- •Задача №6
- •Решение
- •3. Динамика вращательного движения твердого тела. Закон сохранения момента импульса
- •Задача №7
- •Решение
- •Задача №8
- •Решение
- •Задача №9
- •Решение
- •Молекулярная физика.
- •4. Первое начало термодинамики
- •Задача №10
- •Задача№11
- •5. Второе начало термодинамики
- •Задача №12
- •Задача №13
- •Задача №14
- •6. Процессы переноса
- •В равновесном состоянии ,, поэтомуи, а потоки частиц и теплоты обращаются в нуль. Задача №15
- •Решение Задача нахождения величины Dрешается с помощью закона Фика
- •Плотность потока теплоты
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Московский государственный технологический университет «Станкин»
Кафедра «Физика»
А.А. Колоколов «Механика и молекулярная физика»
Методические указания к решению задач
для студентов I-го курса дневного отделения
Москва
2014
УДК
Колоколов А.А.
А.А.Колоколов. – М.: ГОУ ВПО МГТУ «СТАНКИН», 2014. – __с.
Методические указания предназначены для студентов первого курса…
УДК
© Колоколов А.А.
© ГОУ ВПО МГТУ «Станкин», 2014
1. Динамика материальной точки
В
классической нерелятивистской механике,
где скорость движения тел считается
много меньше скорости света в вакууме
![]() ,
основным законом динамики являетсяII-ой
закон Ньютона.
Согласно этому закону в инерциальной
системе отсчета
первая производная импульса
,
основным законом динамики являетсяII-ой
закон Ньютона.
Согласно этому закону в инерциальной
системе отсчета
первая производная импульса
![]() тела по времени
тела по времени![]() равнаполной
силе
равнаполной
силе
![]() ,
действующей на это тело,
,
действующей на это тело,
|
|
(1.0.1) |
Здесь
![]() ,m
– инертная масса тела,
,m
– инертная масса тела,
![]() - мгновенная скорость тела,
- мгновенная скорость тела,![]() - радиус-вектор тела, определяющий его
положение в выбранной инерциальной
системе отсчета.
- радиус-вектор тела, определяющий его
положение в выбранной инерциальной
системе отсчета.
При определении мгновенной скорости тело рассматривается как материальная точка, т.е. линейные размеры тела считаются малыми по сравнению с характерными расстояниями решаемой задачи и не учитывается вращательное движение тела.
Если масса тела m при движении сохраняется постоянной, уравнение (1.0.1) упрощается и принимает вид
|
|
(1.0.2) |
где
![]() - мгновенное ускорение тела. Это
обыкновенное дифференциальное уравнение
второго порядка по времени. Для
однозначного определения решения
уравнения (1.0.2), т.е. нахождения функции
- мгновенное ускорение тела. Это
обыкновенное дифференциальное уравнение
второго порядка по времени. Для
однозначного определения решения
уравнения (1.0.2), т.е. нахождения функции![]() ,
необходимо в некоторый момент времени
,
необходимо в некоторый момент времени![]() задать дваначальных
условия:
задать дваначальных
условия:
|
|
(1.0.3) |
В
этом случае при заданной силе
![]() все последующие состояния тела
все последующие состояния тела![]() ,
,![]() для
для![]() находятся однозначно.
находятся однозначно.
Определение движения тела по заданным начальным условиям и известной силе называется прямой задачей динамики. В обратной задаче требуется найти силу, которая обеспечивает необходимые характеристики движения тела (это задача управления движением тела).
Задача № 1
Два тела с массами m1 и m2 связаны между собой нерастяжимой и невесомой (m=0) нитью, перекинутой через невесомый блок (рис.1.1). Коэффициент трения скольжения между телом 1 и горизонтальной поверхностью μ=0,2. Ускорение свободного падения g=9,8м/с2. Блок считается невесомым. Трением в блоке можно пренебречь. Определить ускорения тел a1 и a2, если в начальный момент времени t=0 они были неподвижны. Рассмотреть два случая: 1) m1=10кг, m2=5кг; 2) m1=10кг, m2=1кг.

Рис.1.1
Решение
Это прямая задача динамики, где по заданным действующим силам необходимо рассчитать движение тел в системе с кинематическими связями. Решение задачи выполняется с помощью следующего алгоритма.
1.
Укажем все силы, которые согласно
условиям задачи действуют на тела
системы с отличной от нуля массой
(движение невесомых тел определяется
связями): силы тяжести
![]() и
и![]() ,
силы натяжения
,
силы натяжения![]() и
и![]() ,
сила реакции опоры
,
сила реакции опоры![]() ,
сила трения
,
сила трения![]() .
.
2. Согласно II-ому закону Ньютона запишем в векторной форме уравнения движения тел 1 и 2:
|
|
(1.1.1) |
|
|
(1.1.2) |
3. Поскольку тела движутся вдоль прямых, то удобно перейти от векторных уравнений к одномерным скалярным уравнениям, используя проекции уравнений (1.1.1)-(1.1.2) на направления соответствующих движений:
|
|
(1.1.3) |
|
|
(1.1.4) |
|
|
(1.1.5) |
В полученные 3 уравнения входят 6 неизвестных величин: a1, a2, T1, T2, N и Fтр. Для однозначного нахождения всех 6 неизвестных систему уравнений (1.1.3)-(1.1.5) необходимо дополнить еще тремя независимыми уравнениями.
4. Для получения дополнительных уравнений воспользуемся условиями задачи и законами физики.
Поскольку нить нерастяжима, то величины ускорений должны быть одинаковыми:
|
|
(1.1.6) |
Нить и блок считаются невесомыми, трение в блоке не учитывается, поэтому величины сил натяжения равны друг другу во всех точках нити:
|
T1=T2=T . |
(1.1.7) |
Сила трения имеет различную физическую природу и величину в зависимости от того, движется тело 1 относительно поверхности или нет:
|
|
(1.1.8) |
Здесь Fтр.п. – сила трения покоя и Fтр.ск. – сила трения скольжения.
В зависимости от условий задачи возможны два решения.
I. Допустим, что действующие силы обеспечивают движение тел и
|
Fтр=Fтр.ск.=μN . |
(1.1.9) |
В этом случае полная система уравнений принимает вид:
|
|
(1.1.10) |
|
|
(1.1.11) |
|
|
(1.1.12) |
Решая эту систему равнений, получим:
|
|
(1.1.13) |
|
|
(1.1.14) |
|
N=m1g . |
(1.1.15) |
Данное решение справедливо, если a>0 или m2>μm1.
Физический
смысл последнего условия заключается
в том, что сила тяжести m2g,
действующая на тело 2, должна превышать
максимальное значение силы трения покоя
![]() =Fтр.ск.=μN=μm1g,
действующей на тело 2 и препятствующей
движению.
=Fтр.ск.=μN=μm1g,
действующей на тело 2 и препятствующей
движению.
II. Если m2<μm1, тела остаются в состоянии покоя и
|
Fтр=Fтр.п. . |
(1.1.16) |
Соответствующая
полная система уравнений принимает вид
(![]() ):
):
|
|
(1.1.17) |
|
|
(1.1.18) |
|
|
(1.1.19) |
Решение этой системы дает:
|
|
(1.1.20) |
|
|
|
Для m1=10кг, m2=5кг и μ=0,2 справедливо условие m2>μm1, поэтому тела движутся с ускорением
|
|
(1.1.21) |
При m1=10кг, m2=1кг и μ=0,2 выполняется условие m2<μm1, сила трения покоя Fтр.п.=m2g и тела остаются в состоянии покоя, когда
|
|
(1.1.21) |
Ответ:
1)
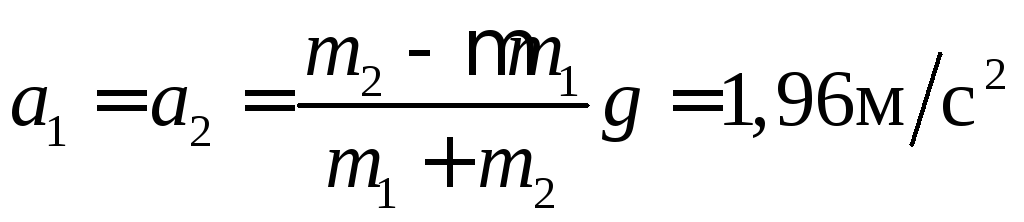 ;
2)
;
2)![]() .
.


 ,
, ,
, .
.