
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
« Магнитогорский государственный технический университет им. Г.И. Носова»
Сыромятников В. Я.
Сыромятникова Т. Н.
Решение примеров и задач в электроприводе
Утверждено Редакционно-издательским советом
университета в качестве практикума
Магнитогорск 2013
Рецензенты:
Сыромятников В. Я., Сыромятникова Т. Н.
Решение примеров и задач в электроприводе: практикум, Магнитогорск: Изд-во Магнитогорск, гос. техн. ун-та им. Г. И. Носова, 2013. 60 с.
В практикуме приведены примеры решения задач в электроприводе. Предназначен для студентов спец. 140211, изучающих дисциплину электропривод.
Оглавление
Расчетные формулы механики электропривода
Для поступательного движения электропривода зависимость между силами сопротивления и движущими силами выражается уравнением:
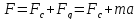 ,
(1)
,
(1)
где
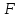 – движущая сила, Н;
– движущая сила, Н;
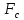 –сила статического
сопротивления, Н;
–сила статического
сопротивления, Н;
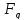 =
=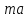 – сила динамического сопротивления,
Н;
– сила динамического сопротивления,
Н;
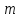 –масса всех
движущихся элементов, приведенная к
определенной точке какого – либо
элемента, кг;
–масса всех
движущихся элементов, приведенная к
определенной точке какого – либо
элемента, кг;
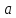 –линейное ускорение
(замедление) точки, к которой приведена
масса, м/с2.
–линейное ускорение
(замедление) точки, к которой приведена
масса, м/с2.
Для вращательного движения уравнение (1) примет вид:
 ,
(2)
,
(2)
где
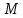 – вращающийся момент двигателя, Н·м;
– вращающийся момент двигателя, Н·м;
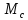 –приведенный к
определенному валу момент статического
сопротивления, Н·м;
–приведенный к
определенному валу момент статического
сопротивления, Н·м;
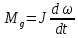 –приведенный к
определенному валу момент динамического
сопротивления, Н·м;
–приведенный к
определенному валу момент динамического
сопротивления, Н·м;
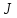 –приведенный к
определенному валу момент инерции всех
движущихся элементов, кг·м2;
–приведенный к
определенному валу момент инерции всех
движущихся элементов, кг·м2;
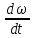 –угловое ускорение
(замедление) вращающегося элемента, к
валу которого приведен момент инерции,
с-2.
–угловое ускорение
(замедление) вращающегося элемента, к
валу которого приведен момент инерции,
с-2.
Если агрегат имеет переменный момент инерции (поршневые машины, подъемная установка с переменным радиусом навивки и др.), то момент на валу определяется уравнением:
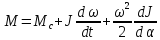 ,
(3)
,
(3)
где
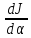 – скорость изменения момента инерции,
приведенного к валу двигателя в
зависимости от угла поворота вала
(углового перемещения)
– скорость изменения момента инерции,
приведенного к валу двигателя в
зависимости от угла поворота вала
(углового перемещения)
Если при установившемся движении известна мощность на валу двигателя и скорость вращения, то статический момент определяют из равенства:
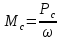 ,
(4)
,
(4)
где
 – мощность, Вт;
– мощность, Вт;
ω – угловая скорость вращения, с-1.
Для определения моментов всех движущихся элементов необходимо произвести опыт свободного выбега, из которого находят:
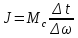 ,
(5)
,
(5)
где
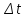 - промежуток времени (с) в течение которого
скорость вращения снизится на
- промежуток времени (с) в течение которого
скорость вращения снизится на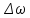 при постоянном
при постоянном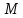 .
.
Если система состоит из вращающихся и поступательно движущихся элементов, то приведенный к валу двигателя статический момент при передаче мощности от двигателя к вращающейся машине определяется уравнением:
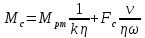 ,
(6)
,
(6)
где
 – статический момент на валу любого
вращающегося элемента, Н·м;
– статический момент на валу любого
вращающегося элемента, Н·м;
 - сила статического
сопротивления, Н;
- сила статического
сопротивления, Н;
 и
и
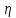 - передаточное число и КПД промежуточных
передач;
- передаточное число и КПД промежуточных
передач;
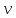 –линейная скорость,
м/с;
–линейная скорость,
м/с;
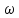 - номинальная
скорость вала двигателя, с-1.
- номинальная
скорость вала двигателя, с-1.
При передаче мощности от рабочей машины к двигателю (спуск груза) в формуле (6) КПД из знаменателя переходит в числитель, т.е.:
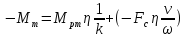 ,
(7)
,
(7)
или точнее формула имеет вид:
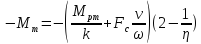 ,
(7а)
,
(7а)
Когда статический момент на валу рабочей машины отличается от номинального, КПД зубчатой передачи можно определить по кривым (рис.1) зависимости КПД передачи от коэффициента загрузки (а).
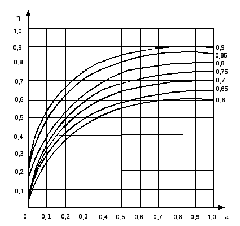 Рисунок
1
Рисунок
1
Приведенный к валу двигателя момент инерции:
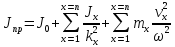 ,
(8)
,
(8)
где
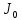 - момент инерции ротора (якоря) двигателя,
кг/м2;
- момент инерции ротора (якоря) двигателя,
кг/м2;
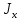 - момент инерции
любого вращающегося элемента;
- момент инерции
любого вращающегося элемента;
 - масса любого
элемента, движущегося поступательно,
кг.
- масса любого
элемента, движущегося поступательно,
кг.
Для приведения вращательного движения к поступательному необходимо определить приведенную массу, которую обычно, приводят к окружности какого – либо вращающегося элемента:
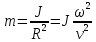 (9)
(9)
Если агрегат состоит из упругих элементов, имеющих различную скорость, то приведенный к валу двигателя коэффициент жесткости определяется уравнением:
 ,
(10)
,
(10)
где
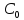 - коэффициент жесткости вала двигателя,
Н·м/рад;
- коэффициент жесткости вала двигателя,
Н·м/рад;
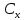 - коэффициент
жесткости элементов, имеющих скорость
отличную от скорости вала двигателя,
Н·м/рад.
- коэффициент
жесткости элементов, имеющих скорость
отличную от скорости вала двигателя,
Н·м/рад.
При параллельном соединении упругих элементов, приведенный коэффициент жесткости:
 (11)
(11)
Предварительное определение оптимального передаточного числа между двигателем и рабочей машиной в отношении минимальной продолжительности пуска и останова при постоянном статическом моменте и равномерно – ускоренном движении производится по формулам:
– для периода пуска:
 ,
(12а)
,
(12а)
– для периода замедления:
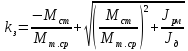 ,
(12б)
,
(12б)
где
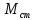 – статический момент на валу рабочей
машины, Н·м;
– статический момент на валу рабочей
машины, Н·м;
 –средний пусковой
момент, Н·м;
–средний пусковой
момент, Н·м;
 - средний момент
торможения за время останова, Н·м;
- средний момент
торможения за время останова, Н·м;
 –момент инерции
рабочей машины на ее валу, кг·м2;
–момент инерции
рабочей машины на ее валу, кг·м2;
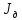 - момент инерции
ротора двигателя, кг·м2.
- момент инерции
ротора двигателя, кг·м2.
Обычно принимают среднее значение:
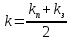 (12в)
(12в)
