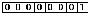3.7. Преобразование дополнительного кода отрицательного числа в обратный и прямой коды

Так как в дополнительном коде значащие разряды отрицательного числа имеют количественный эквивалент qⁿ–|N|, то для определения значащих разрядов

• прямого кода достаточно вычислить

• обратного кода достаточно вычислить

Рассмотрим преобразования на примерах. Вычисляется прямой код в соответствии с первой формулой. Из константы qⁿ вычитаются значащие разряды дополнительного кода числа. Знаковый разряд копируется. Формат значащих разрядов результата расширяется до формата константы.

В следующем примере в вариантах A,B,C и D вычисляется прямой код в соответствии со второй формулой. Для получения значения выражения (qⁿ–q^m)–(qⁿ–|N|) цифры значащих разрядов дополнительного кода числа заменяются на обратные им. К полученному коду значащих разрядов прибавляется q^m, причем перенос из старшего значащего разряда фиксируется в дополнительном старшем значащем разряде результата. Знаковый разряд исходного кода копируется в знаковый разряд результата.

В вариантах E,F,G и H вычисляется прямой код в соответствии с третьей формулой. Выполняется вычитание из значащих разрядов дополнительного кода значения q^m, причем заем из старшего значащего разряда фиксируется в дополнительном старшем значащем разряде результата. Цифры значащих разрядов промежуточной разности заменяются на обратные им.

Знаковый разряд исходного кода копируется в знаковый разряд результата.

В следующем примере вычисляется обратный код в соответствии с четвертой формулой. С целью расширения разрядной сетки результата к значащим разрядам дополнительного кода приписывается слева цифра с количественным эквивалентом q–1, что не изменяет количественный эквивалент дополнительного кода. Из расширенного дополнительного кода вычитается q^m. Знаковый разряд исходного кода можно копировать в знаковый разряд результата.

3.8. Некоторые возможности упрощения преобразований двоичного прямого или обратного кода в дополнительный и наоборот

В двоичной системе счисления цифры в младшем разряде прямого и дополнительного кода совпадают всегда. Цифры младшего разряда обратного и дополнительного кода инверсные. Эти свойства двоичной системы счисления позволяют упростить любые из рассмотренных выше вариантов взаимных преобразований кодов: прямой – дополнительный и обратный – дополнительный.

Прямой код отрицательных чисел

В знаковый разряд помещается цифра 1, а в разряды цифровой части числа – двоичный код его абсолютной величины.

Пример (при n = 8):

Прямой код числа –1

Прямой код числа –127

Диапазон представимых чисел: –(2^n–1–1)...0.

Обратный код отрицательных чисел

Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы – нулями.

Пример (n = 8):

Число: –1 Код модуля числа: Обратный код числа:

Число: –127 Код модуля числа: Обратный код числа:

Диапазон представимых чисел: –(2^n–1–1)…0.

Дополнительный код отрицательных чисел

Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду. Например:

Дополнительный код числа –1:

Дополнительный код числа –127:

Другой способ – перевод прямого кода отрицательного двоичного числа в дополнительный. Определяется следующим правилом: оставить без изменения все младшие нули и одну младшую единицу, остальные разряды (кроме знакового!) проинвертировать.

Исключение из правила: код 1|00…0 (–0) следует замещать кодом 0|00…0 (+0). Например:

X_пр: 1|0010000 1|1011100 1|1011001 1|1000000 1|0000000

X_доп: 1|1110000 1|0100100 1|0100111 1|1000000 0|0000000

Для преобразования дополнительного кода отрицательного двоичного числа в прямой код достаточно инвертировать цифры значащих разрядов дополнительного кода, кроме цифры младшего разряда, и, если младший разряд равен 0, прибавить 1 ко второму разряду полученного кода. Дополнительный старший значащий разряд результата принять равным 0 или значению переноса из старшего значащего разряда, если выполнялось сложение.

Диапазон представимых чисел: –2^n–1...–1.