3. Способы представления чисел (прямой, обратный и дополнительный коды)

В целях упрощения выполнения арифметических операций и определения знака результата применяют специальные коды для представления чисел. Операция вычитания (или алгебраического сложения) чисел сводится к арифметическому сложению кодов, облегчается выработка признаков переполнения разрядной сетки. В результате упрощаются устройства, выполняющие арифметические операции.

Для представления чисел со знаком в ЭВМ применяют прямой, обратный и дополнительный коды.

Общая идея построения кодов такова. Код трактуется как число без знака, а диапазон представляемых кодами чисел без знака разбивается на два поддиапазона. Один из них представляет положительные числа, другой – отрицательные. Разбиение выполняется таким образом, чтобы принадлежность к поддиапазону определялась максимально просто.

Наиболее распространенным и удобным является формирование кодов таким образом, чтобы значение старшего разряда указывало на знак представляемых чисел, т.е. использование такого кодирования позволяет говорить о старшем разряде как о знаковом (бит знака) и об остальных как о цифровых разрядах кода.

Для представления знаковых целых чисел используются три способа:

1) прямой код;

2) обратный код;

3) дополнительный код.

Все три способа используют самый левый (старший) разряд битового набора длины n для кодирования знака числа: знак «плюс» кодируется нулем, а «минус» – единицей. Остальные n–1 разрядов (называемые мантиссой или цифровой частью) используются для представления абсолютной величины числа.

Запись числа α_nα_n–1…α_i…α₁α₀α_–1…α_m , где α_n∈{0,1} – знак числа, при всех прочих равных условиях имеет разные количественные эквиваленты в зависимости от того в каком коде, прямом, обратном или дополнительном, оно записано.

3.1. Положительные целые числа

Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково – цифровая часть содержит двоичную запись числа (значащие разряды α_n–1÷α_m кодируют количественный эквивалент числа), в знаковом разряде содержится 0. Например, для n = 8:

110=12

12710=11111112

Диапазон представимых чисел: 0…2^n–1–1.

3.2. Отрицательные целые числа

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.

Значащие разряды α_n–1÷α_m отрицательного числа N кодируют:

• в прямом коде – модуль количественного эквивалента |N|;

• в обратном коде – дополнение модуля количественного эквивалента до веса знакового разряда, уменьшенного на вес младшего разряда, т.е. величину (qⁿ–q^m)–|N|;

• в дополнительном коде – дополнение модуля количественного эквивалента до веса знакового разряда qⁿ, т.е. величину qⁿ–|N|.

Например, число –137 в десятичной q = 10 и в двоичной q = 2 системах счислениях в разных кодах записывают так:

1|137_пр 1|862_обр 1|863_доп

1|10001001_пр 1|01110110_обр 1|01110111_доп

Формулы для вычисления количественного эквивалента кода

• прямого

• дополнительного

• обратного

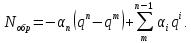
Прямой, обратный и дополнительный коды обладают следующими свойствами:

1. В прямом и обратном кодах число ноль можно записать двумя способами. В прямом коде: 0|0₁₀ или 1|0₁₀; 0|00...0₂ или 1|00...0₂.

В обратном коде: 0|0₁₀ или 1|9₁₀; 0|00...0₂ или 1|11...1₂.

2. В прямом и обратном кодах диапазоны представления положительных и отрицательных чисел одинаковы и симметричны относительно нуля. Модуль минимального числа равен максимальному числу.

3. Сложение положительного числа с его отрицательным значением в обратном коде дает так называемую машинную единицу (МЕ_обр) 1|9₁₀ (1|11...1₂), состоящую из единиц в знаковом и значащих разрядах числа. Значение отрицательного нуля совпадает с МЕ_обр.

4. В дополнительном коде число ноль можно записать только одним способом как 0|0₁₀ (0|00...0₂) – машинный ноль. Отрицательный ноль в дополнительном коде не существует.

5. В дополнительном коде диапазоны представления положительных и отрицательных чисел не симметричны относительно нуля. Модуль минимального числа превышает максимальное число на величину равную весу младшего разряда q^m. Код минимального числа в дополнительном коде 1|00...0 при любом натуральном q, а его количественный эквивалент – qⁿ.

6. В дополнительном коде сумма положительного и равного ему по абсолютному значению отрицательного числа равна машинному нулю.

7. Минимальное число представимое в дополнительном коде (–qⁿ) нельзя записать в прямом или в обратном коде, сохранив разрядность кодов.