1. Системы счисления
Под системой счисления понимают способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами. Существуют различные системы счисления. От их особенностей зависят наглядность представления числа при помощи цифр и сложность выполнения арифметических операций.
Любая предназначенная для практического применения система счисления должна обеспечивать:
возможность представления любого числа в рассматриваемом диапазоне величин;
единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);
простоту оперирования числами.
Системы счисления подразделяются на позиционные и непозиционные. Обе системы счисления используют определённый набор символов – цифр.
Последовательное сочетание цифр образует число.
Непозиционная система счисления – система счисления, в которой для обозначения чисел вводятся специальные знаки, количественное значение которых («вес» символа) всегда одинаково и не зависит от их места в записи числа.
Классическим примером такой системы счисления является римская. В ней для записи чисел используются буквы латинского алфавита. При этом буква I означает единицу, V – пять, Х – десять, L – пятьдесят, С – сто, D – пятьсот, М – тысячу.
Для записи чисел в римской системе используются два правила:
1) каждый меньший знак, поставленный слева от большего, вычитается из него;
2) каждый меньший знак, поставленный справа от большего, прибавляется к нему.
|
III = 1+1+1 = 3 |
IV = –1+5 = 4 |
VI = 5+1 = 6 |
|
XL = –10+50 = 40 |
LX = 50+10 = 60 |
XC = –10+100 = 90 |
|
CIX = 100–1+10 = 109 MCMXCVIII = 1000–100+1000–10+100+5+1+1+1=1998 | ||
Позиционной системой счисления называется система счисления, в которой значение каждой цифры в изображении числа зависит от ее положения в ряду других цифр, изображающих число.
В позиционной системе счисления количество символов в наборе равно основанию системы счисления.
Место каждой цифры в числе называется позицией.
Номер позиции символа в числе называется разрядом.
Количество различных цифр, используемых для представления чисел, называют основанием системы счисления.
Для позиционной системы счисления справедливо равенство (полином):
где A(q) – произвольное число, записанное в системе счисления с основанием q; ai – коэффициенты ряда (цифры системы счисления); n, m – количество целых и дробных разрядов.
На практике используют сокращенную цифровую запись чисел – последовательность цифр, разделенных запятой на две группы: группу разрядов, изображающую целую часть числа, и группу разрядов, изображающую дробную часть числа:
где а0, а1… – цифры нулевого, первого и т.д. разрядов целой части числа;
а–1, а–2… – цифры первого, второго и т.д. разрядов дробной части числа.
При этом всегда выполняется неравенство:
Единице каждого разряда целой части числа приписан определенный вес
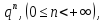
а единице каждого разряда дробной части числа –
где n и m – номера разрядов, равные индексам при буквах, изображающих цифры разрядов.
Таблица 1
Представление чисел в различных системах счисления
|
Система счисления |
Цифровая форма |
Многочленная форма |
|
Двоичная (q = 2) |
11010,1012 |
1·24+1·23+0·22+1·21+0·20+1·2–1+0·2–2+1·2–3 |
|
Троичная (q = 3) |
22120,2123 |
2·34+2·33+1·32+2·31+0·30+2·3–1+1·3–2+2·3–3 |
|
Восьмеричная (q = 8) |
3714,43148 |
3·83+7·82+1·81+4·80+4·8–1+3·8–2+1·8–3+4·8–4 |
|
Десятичная (q = 10) |
4509,5210 |
4·103+5·102+0·101+9·100+5·10–1+2·10–2 |
|
Шестнадцатеричная (q = 16) |
A3F,1CD16 |
A·162+3·161+F·160+1·16–1+C·16–2+D·16–3 |
Для получения числа в некоторой позиционной системе счисления необходимо сложить произведения значений цифр на степени оснований, показатели которых равны номерам разрядов (табл.1). Одно и то же число в зависимости от основания q системы счисления при кодировании формируется из разного количества разрядов.
Для кодирования заданного диапазона чисел в машине в зависимости от выбранной системы счисления требуется разное количество оборудования.
Определим, при каком основании q0 для представления данного множества чисел М требуется наименьшее количество аппаратуры (аппаратных затрат). Множество чисел
Предположим, что объём используемых электронных элементов для обработки каждого разряда пропорционален основанию системы счисления. Тогда для реализации множества чисел (4) потребуется N электронных схем:
где α – коэффициент пропорциональности, q – основание системы счисления, n – количество разрядов.
Так как
Подставим (**) в выражение (*).
Поскольку N есть функция q при прочих постоянных значениях, для определения q0 найдём и приравняем нулю первую производную:
Таким образом, наиболее экономичным основанием позиционной системы счисления является число e = 2,718.
Из целочисленных значений оснований ближайшими к значению e являются цифры 2 и 3. Код с нецелым основанием q технически нереализуем. По соображениям простоты технической реализации явное преимущество на стороне кода с q = 2. Для него необходимы дискретные элементы с двумя устойчивыми состояниями (триггеры). Кроме двоичной системы в вычислительной технике используются позиционные системы счисления с основанием q кратным 2:
восьмеричная;
шестнадцатеричная;
двоично-десятичная.ованием стемы счисления является число
скольку p.выражение для ения, М=ов для обработки каждого разряда пропорционален основаниюппаратных затрат).