Вычисление контрольных битов для кода (7,4)

ПОЗИЦИЯ КОДА	КОНТРОЛЬНЫЕ БИТЫ
	С3	С2	С1
3 бит (М1)	0	1	1
5 бит (М2)	1	0	1
6 бит (М3)	1	1	0
7 бит (М4)	1	1	1
СУММИРУЕМЫЕ ПО МОДУЛЮ 2 БИТЫ	М2 М3 М4	М1 М3 М4	М1 М2 М4

Таким образом, передатчик вычисляет значения контрольных разрядов по следующим логическим выражениям:

С₁=М₁⊕М₂⊕М₄;

С₂=М₁⊕М₃⊕М₄;

С₃=М₂⊕М₃⊕М₄.

Приемник проверяет правильность принятого кода, вычисляя следующие выражения:

С₁₁=С₁⊕М₁⊕М₂⊕М₄;

С₁₂=С₂⊕М₁⊕М₃⊕М₄;

С₁₃=С₃⊕М₂⊕М₃⊕М₄.

Построим код Хэмминга для передачи семибитового кода.

Условие 1. Это условие будет выполняться при N=11:

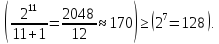
Таким образом, для семи информационных битов (М=7), требуются четыре контрольных бита (С=4).

Условие 2. Определяем местоположение информационных и контрольных битов в коде.

Положение информационных и контрольных битов	M7	M6	M5	C4	M4	M3	M2	C3	M1	C2	C1
Номер позиции кода	11	10	9	8	7	6	5	4	3	2	1

Условие 3. Определяем логические выражения для вычисления контрольных битов. Для этого построим таблицу.

Таблица 2

Вычисление контрольных битов для кода (11,4)

ПОЗИЦИЯ КОДА	КОНТРОЛЬНЫЕ БИТЫ
	С4	С3	С2	С1
3 бит (М1)	0	0	1	1
5 бит (М2)	0	1	0	1
6 бит (М3)	0	1	1	0
7 бит (М4)	0	1	1	1
9 бит (М5)	1	0	0	1
10 бит (М6)	1	0	1	0
11 бит (М7)	1	0	1	1
СУММИРУЕМЫЕ ПО МОДУЛЮ 2 БИТЫ	М5 М6 М7	М2 М3 М4	М1 М3 М4 М6 М7	М1 М2 М4 М5 М7

Таким образом, передатчик вычисляет значения контрольных разрядов по следующим логическим выражениям:

С₁=М₁⊕М₂⊕М₄⊕М₅⊕М₇;

С₂=М₁⊕М₃⊕М₄⊕М₆⊕М₇;

С₃=М₂⊕М₃⊕М₄;

С₄=М₅⊕М₆⊕М₇.

Приемник проверяет правильность передачи кода, вычисляя следующие выражения:

С₁₁=С₁⊕М₁⊕М₂⊕М₄⊕М₅⊕М₇;

С₁₂=С₂⊕М₁⊕М₃⊕М₄⊕М₆⊕М₇;

С₁₃=С₃⊕М₂⊕М₃⊕М₄;

С₁₄=С₄⊕М₅⊕М₆⊕М₇.

Рассмотрим примеры передачи информации с использованием кода Хэмминга для случаев, когда ошибки при передаче нет, и когда есть.

Начнем с кода (7,4).

Пример. В канал связи нужно передать следующий блок информации: 1101₂.

Передатчик формирует код Хэмминга:

M4	M3	M2	C3	M1	C2	C1
1	1	0	*	1	*	*

С₁=М₁⊕М₂⊕М₄=1⊕0⊕1=0;

С₂=М₁⊕М₃⊕М₄=1⊕1⊕1=1;

С₃=М₂⊕М₃⊕М₄=0⊕1⊕1=0,

тогда код, передаваемый в канал, будет:

M4	M3	M2	C3	M1	C2	C1
1	1	0	0	1	1	0

Рассмотрим случай, когда не было ошибки при передаче кода.

Тогда точно такой же код принял приемник. Теперь приемник проверяет правильность передачи кода, вычисляя следующие выражения:

С₁₁=С₁⊕М₁⊕М₂⊕М₄=0⊕1⊕0⊕1=0;

С₁₂=С₂⊕М₁⊕М₃⊕М₄=1⊕1⊕1⊕1=0;

С₁₃=С₃⊕М₂⊕М₃⊕М₄=0⊕0⊕1⊕1=0.

Поскольку значение, составленное из контрольных битов, равно нулю, ошибки нет, и код передается от приемника далее.

Рассмотрим случай, когда была ошибка при передаче кода.

Пусть ошибка произошла в третьем бите, т.е. принят код:

M4 4	M3 3	M2 2	C3 3	M1 1	C2 2	C1 1
1	1	0	0	0	1	0

Теперь приемник проверяет правильность передачи кода, вычисляя следующие выражения:

С₁₁=С₁⊕М₁⊕М₂⊕М₄=0⊕0⊕0⊕1=1;

С₁₂=С₂⊕М₁⊕М₃⊕М₄=1⊕0⊕1⊕1=1;

С₁₃=С₃⊕М₂⊕М₃⊕М₄=0⊕0⊕1⊕1=0.

Поскольку, значение, составленное из контрольных разрядов, равно 011₂, ошибка в бите № 3. Приемник меняет значение этого бита на противоположное.

Теперь рассмотрим код (11,7).

Пример. В канал связи нужно передать следующий блок информации: 1101010₂.

Передатчик формирует код Хэмминга:

M7	M6	M5	C4	M4	M3	M2	C3	M1	C2	C1
1	1	0	*	1	0	1	*	0	*	*

С₁=М₁⊕М₂⊕М₄⊕М₅⊕М₇=0⊕1⊕1⊕0⊕1=1;

С₂=М₁⊕М₃⊕М₄⊕М₆⊕М₇=0⊕0⊕1⊕1⊕1=1;

С₃=М₂⊕М₃⊕М₄=1⊕0⊕1=0;

С₄=М₅⊕М₆⊕М₇=0⊕1⊕1=0,

тогда код, передаваемый в канал, будет:

M7	M6	M5	C4	M4	M3	M2	C3	M1	C2	C1
1	1	0	0	1	0	1	0	0	1	1

Рассмотрим случай, когда не было ошибки при передаче кода.

Тогда точно такой же код принял приемник. Теперь приемник проверяет правильность передачи кода, вычисляя следующие выражения:

С₁₁=С₁⊕М₁⊕М₂⊕М₄⊕М₅⊕М₇=1⊕0⊕1⊕1⊕0⊕1=0;

С₁₂=С₂⊕М₁⊕М₃⊕М₄⊕М₆⊕М₇=1⊕0⊕0⊕1⊕1⊕1=0;

С₁₃=С₃⊕М₂⊕М₃⊕М₄=0⊕1⊕0⊕1=0;

С₁₄=С₄⊕М₅⊕М₆⊕М₇=0⊕0⊕1⊕1=0.

Поскольку значение, составленное из контрольных битов, равно нулю, ошибки нет, и код передается от приемника далее.

Рассмотрим случай, когда была ошибка при передаче кода.

Пусть ошибка произошла во втором бите, т.е. принят код:

M7	M6	M5	C4	M4	M3	M2	C3	M1	C2	C1
1	1	0	0	1	0	1	0	0	0	1

Теперь приемник проверяет правильность передачи кода, вычисляя следующие выражения:

С₁₁=С₁⊕М₁⊕М₂⊕М₄⊕М₅⊕М₇=1⊕0⊕1⊕1⊕0⊕1=0;

С₁₂=С₂⊕М₁⊕М₃⊕М₄⊕М₆⊕М₇=0⊕0⊕0⊕1⊕1⊕1=1;

С₁₃=С₃⊕М₂⊕М₃⊕М₄=0⊕1⊕0⊕1=0;

С₁₄=С₄⊕М₅⊕М₆⊕М₇=0⊕0⊕1⊕1=0.

Поскольку значение, составленное из контрольных битов, равно 0010₂, ошибка во втором бите. Приемник меняет значение этого бита на противоположное.

Код Хэмминга является равномерно защищенным, исправляет ошибки как в информационных, так и в контрольных битах. С его помощью возможно исправление одиночной и обнаружение двойной ошибки. Для того чтобы обнаружить двойную ошибку, в код Хэмминга вводят дополнительный контрольный бит E₀. Значение E₀ вычисляется как сумма по модулю 2 всех разрядов кода Хэмминга, т.е. он дополняет код Хэмминга по четности. На стороне приемника, кроме получения контрольных разрядов, которые определяют позицию с ошибкой, вычисляется контрольный разряд E₁₀:

E₁₀=Е₀⊕<сложенные по модулю 2 все остальные биты принятого кода>.

Если E₁₀=0, то ошибок нет. Если значение, полученное из контрольных разрядов, не равно 0 и E₁₀=1, то имеет место одиночная ошибка, позиция которой определяется значением контрольных разрядов. Если значение С≠0 и E₁₀=0 , то имеет место двойная ошибка.

Рассмотрим пример для кода, исправляющего одиночную ошибку и обнаруживающего двойную.

Для кода (11,7) формат блока информации:

M7

M6

M5

C4

M4

M3

M2

C3

M1

C2

C1

Е0

Пример. В канал связи нужно передать следующий блок информации: 1101010₂.

Передатчик формирует код Хэмминга:

M7	M6	M5	C4	M4	M3	M2	C3	M1	C2	C1	Е0
1	1	0	*	1	0	1	*	0	*	*	*

С₁=М₁⊕М₂⊕М₄⊕М₅⊕М₇=0⊕1⊕1⊕0⊕1=1;

С₂=М₁⊕М₃⊕М₄⊕М₆⊕М₇=0⊕0⊕1⊕1⊕1=1;

С₃=М₂⊕М₃⊕М₄=1⊕0⊕1=0;

С₄=М₅⊕М₆⊕М₇=0⊕1⊕1=0,

Е₀=С₁⊕С₂⊕М₁⊕С₃⊕М₂⊕М₃⊕М₄⊕С₄⊕М₅⊕М₆⊕М₇=1⊕1⊕0⊕0⊕1⊕0⊕⊕1⊕0⊕0⊕1⊕1=0,

тогда код, передаваемый в канал, будет:

M7	M6	M5	C4	M4	M3	M2	C3	M1	C2	C1	Е0
1	1	0	0	1	0	1	0	0	1	1	0

Рассмотрим случай, когда не было ошибки при передаче кода.

Тогда точно такой же код принял приемник. Теперь приемник проверяет правильность передачи кода, вычисляя следующие выражения:

С₁₁=С₁⊕М₁⊕М₂⊕М₄⊕М₅⊕М₇=1⊕0⊕1⊕1⊕0⊕1=0;

С₁₂=С₂⊕М₁⊕М₃⊕М₄⊕М₆⊕М₇=1⊕0⊕0⊕1⊕1⊕1=0;

С₁₃=С₃⊕М₂⊕М₃⊕М₄=0⊕1⊕0⊕1=0;

С₁₄=С₄⊕М₅⊕М₆⊕М₇=0⊕0⊕1⊕1=0,

Е₁₀= Е₀⊕С₁⊕С₂⊕М₁⊕С₃⊕М₂⊕М₃⊕М₄⊕С₄⊕М₅⊕М₆⊕М₇=

=0⊕1⊕1⊕0⊕0⊕1⊕0⊕1⊕0⊕0⊕1⊕1=0.

Поскольку значение, составленное из контрольных битов, равно 0, и Е₁₀=0, ошибки нет, и код передается от приемника далее.

Рассмотрим случай, когда была одиночная ошибка при передаче кода.

Пусть ошибка произошла во втором бите (не считая Е₀, т.е. в С₂) и принят код:

M7	M6	M5	C4	M4	M3	M2	C3	M1	C2	C1	Е0
1	1	0	0	1	0	1	0	0	0	1	0

Теперь приемник проверяет правильность передачи кода, вычисляя следующие выражения:

С₁₁=С₁⊕М₁⊕М₂⊕М₄⊕М₅⊕М₇=1⊕0⊕1⊕1⊕0⊕1=0;

С₁₂=С₂⊕М₁⊕М₃⊕М₄⊕М₆⊕М₇=0⊕0⊕0⊕1⊕1⊕1=1;

С₁₃=С₃⊕М₂⊕М₃⊕М₄=0⊕1⊕0⊕1=0;

С₁₄=С₄⊕М₅⊕М₆⊕М₇=0⊕0⊕1⊕1=0,

Е₁₀= Е₀⊕С₁⊕С₂⊕М₁⊕С₃⊕М₂⊕М₃⊕М₄⊕С₄⊕М₅⊕М₆⊕М₇=

=0⊕1⊕0⊕0⊕0⊕1⊕0⊕1⊕0⊕0⊕1⊕1=1.

Поскольку значение Е₁₀=1 и значение, составленное из контрольных разрядов, равно 0010₂, то ошибка во втором бите. Приемник меняет значение этого бита на противоположное.

Рассмотрим случай, когда была двойная ошибка при передаче кода.

Пусть ошибка произошла во втором (т.е. в С₂) и в пятом битах (т.е. М₂) и принят код:

M7	M6	M5	C4	M4	M3	M2	C3	M1	C2	C1	Е0
1	1	0	0	1	0	0	0	0	0	1	0

Теперь приемник проверяет правильность передачи кода, вычисляя следующие выражения:

С₁₁=С₁⊕М₁⊕М₂⊕М₄⊕М₅⊕М₇=1⊕0⊕0⊕1⊕0⊕1=1;

С₁₂=С₂⊕М₁⊕М₃⊕М₄⊕М₆⊕М₇=0⊕0⊕0⊕1⊕1⊕1=1;

С₁₃=С₃⊕М₂⊕М₃⊕М₄=0⊕0⊕0⊕1=1;

С₁₄=С₄⊕М₅⊕М₆⊕М₇=0⊕0⊕1⊕1=0,

Е₁₀= Е₀⊕С₁⊕С₂⊕М₁⊕С₃⊕М₂⊕М₃⊕М₄⊕С₄⊕М₅⊕М₆⊕М₇=

=0⊕1⊕0⊕0⊕0⊕0⊕0⊕1⊕0⊕0⊕1⊕1=0.

Поскольку значение Е₁₀=0 и значение, составленное из контрольных разрядов, равно 0111₂≠0, то произошла двойная ошибка. Приемник не передает код далее, а запрашивает от источника повторную передачу этого блока информации.