Непозиционные системы счислен (например, римская)
I – единица, V – пять, Х – десять,
L – пятьдесят, С – сто, D –
пятьсот, |
IV = –1+5 = 4 |
VI = 5+1 = 6 |
||
III = 1+1+1 = 3 |
|
|||
XL = |
тысяча |
XC = –10+100 = 90 |
||
|
–10+50 = |
40 LX = 50+10 = 60 |
||
CIX = 100–1+10 = 109
MCMXCVIII = 1000–100+1000–10+100+5+1+1+1=1998
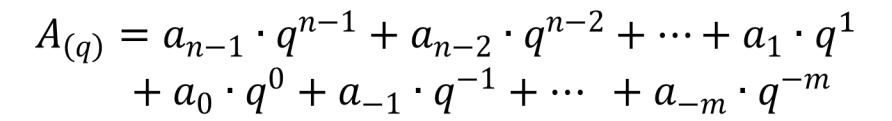
Позиционные системы счисления
A(q) – произвольное число, записанное в системе счисления с основанием q;
ai – коэффициенты ряда (цифры системы
счисления); n, m – количество целых и дробных разрядов.
Позиционные системы счисления
Представление чисел в различных системах счисления
Система счисления
Двоичная (q=2) Троичная (q=3) Восьмеричная (q=8) Десятичная (q=10)
Шестнадцатеричная
(q=16)
Цифровая
форма 
11010,1012
22120,2123
3714,43148 
4509,5210
A3F,1CD16
Многочленная форма
1·24+1·23+0·22+1·21+0·20+1·2–1+0·2–2+1·2–3 2·34+2·33+1·32+2·31+0·30+2·3–1+1·3–2+2·3–3 3·83+7·82+1·81+4·80+4·8–1+3·8–2+1·8–3+4·8–4 
4·103+5·102+0·101+9·100+5·10–1+2·10–2
A·162+3·161+F·160+1·16–1+C·16–2+D·16–3
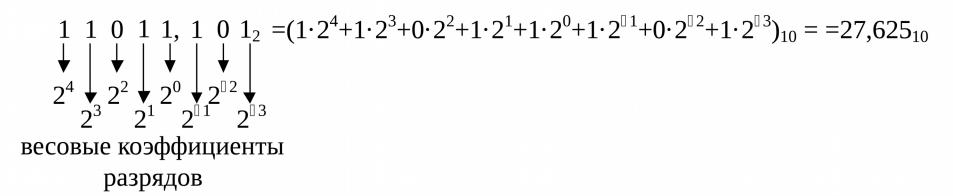
Двоичная система счисления
Основание системы счисления: q = 2 Алфавит системы счисления: 0, 1
Восьмеричная система счисления
снование системы счисления: q = 8 фавит системы счисления: 0, 1, 2, 3, 4, 5,
Десятичная система счисления
ование системы счисления: q = 10
ит системы счисления: 0, 1, 2, 3, 4, 5, 6,
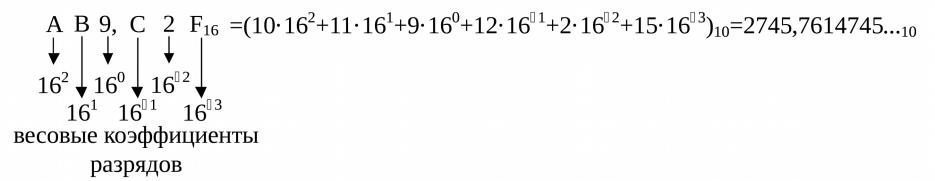
естнадцатеричная система счисле
ование системы счисления: q = 16
ит системы счисления: 0, 1, 2, 3, 4, 5, 6,
, D, E, F
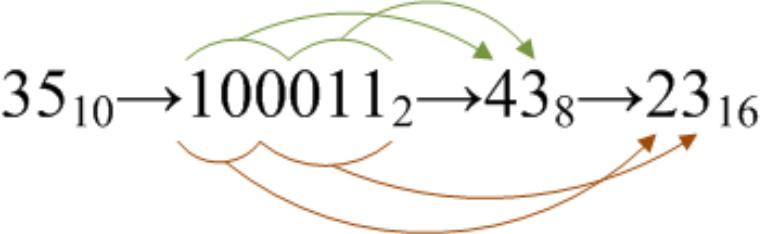
Связь между системами счисления
D |
B |
Q |
H |
D |
B |
Q |
H |
0 |
0 |
0 |
0 |
9 |
1001 |
11 |
9 |
1 |
1 |
1 |
1 |
10 |
1010 |
12 |
A |
2 |
10 |
2 |
2 |
11 |
1011 |
13 |
B |
3 |
11 |
3 |
3 |
12 |
1100 |
14 |
C |
4 |
100 |
4 |
4 |
13 |
1101 |
15 |
D |
5 |
101 |
5 |
5 |
14 |
1110 |
16 |
E |
6 |
110 |
6 |
6 |
15 |
1111 |
17 |
F |
7 |
111 |
7 |
7 |
16 |
10000 |
20 |
10 |
8 |
1000 |
10 |
8 |
17 |
10001 |
21 |
11 |
еревод из D в B, Q, H (целая часть
