2.3. Передаточные функции сау

Понятие передаточной функции является очень важной кате­горией в теории автоматического управления и регулирования. Переда­точная функция является своего рода математической моделью САР, т.к. полностью характеризует динамические свойства системы.

Под передаточной функцией элемента или системы понимают от­ношение операторного (лапласового) изображения соответствующей вы­ходной величины к операторному изображению входной величины.

При этом также считают, что элемент или система находились при ну­левых начальных условиях, т.е. элемент или система находились в уста­новившемся состоянии, т.е. в состоянии покоя.

Следовательно, передаточная функция определяется в виде отношения

. (2.8)

Для системы, описываемой операторным уравнением (2.7), переда­точная функция будет иметь следующий вид:

. (2.9)

Следовательно, передаточная функция W(p) равна отношению двух полиномов:

, (2.10)

. (2.11)

Как видно из уравнения (2.9), передаточная функция является дробно-рациональной функцией от независимого переменного р. Числитель пе­редаточной функции является левой частью уравнения элемента или сис­темы, а знаменатель - правой частью.

Уравнение

(2.12)

является характеристическим уравнением дифференциального уравнения, а поэтому оно также называется характеристическим уравнением звена. Поэтому D(p) называется характеристическим полиномом звена.

В системах автоматического управления степень полинома знамена­теля в выражении (2.9) всегда выше или равна степени полинома числи­теля, т.е. m≤n.

Из приведенных соотношений также видно, что передаточную функ­цию легко получить из дифференциального уравнения простой формаль­ной заменой производных оператором p в соответствующей степени.

Из выражения (2.8) следует, что изображение выходной величины оп­ределяется передаточной функцией и изображением входной величины

. (2.13)

Запись соотношений между выходом и входом звена в виде последнего уравнения (2.13) имеет большое практическое значение и дает значительное

преимущество при исследовании САР, т.к. оно позволяет графически изобразить звено следующим образом (рис. 2.1).

В замкнутых САР имеется сложное взаимодействие блоков: выход одного блока может служить входом другого блока и т.д.

Использование понятия передаточной функции звеньев позволяет без особого труда находить связь между лю­быми координатами всей системы на основании знания передаточных функций соответствующих звеньев, составляющих эту систему. Не пред­ставляет трудности при этом и составление общего графического изображе­ния ее в виде структурной схемы.

Рассмотрим также в общем виде очень важное понятие коэффи­циента передачи (коэффициента усиления) К в установившемся режиме для звена с произвольной передаточной функцией W(p).

Если на вход звена подать постоянный входной сигнал X_вх.у, то выходной сигнал Х_вых(t) при t→∞, будет стремиться к некоторому установившемуся значению .

Тогда по определению

. (2.14)

Или считая, что в установившемся режиме все производные становятся равными нулю, получим выражение для передаточной функции (2.9.)

. (2.15)

Следовательно, при р=0 передаточная функция вырождается в обычный коэффициент усиления элемента или системы.

Пример

Представить математическое описание и передаточную функцию для R-L цели, представленной на рис. 2.2.

Решение

Для R-L цепи можно представить следующее дифференциальное уравнение:

, (2.16)

. (2.17)

Решив уравнение (2.17) относительно тока i и подставив в уравнение (2.16), получим

или

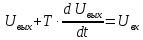, (2.18)

где -постоянная времени R-L цепи.

Представим уравнение (2.18) в операторном виде

или

.

Отсюда передаточная функция данного звена будет иметь вид