4.3.3.Передаточная функция системы, охваченной обратной связью

Обратная связь может быть положительной, если сигнал об­ратной связи Х_ос суммируется со входным сигналом Х_вх , или отрицательной, если Х_ос вычитается из Х_вх (минус у суммирующего элемента). Для замкнутой системы (рис. 4.7) можно записать уравнение:

;

; (4.16)

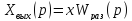
где W_oc(p) - передаточная функция звена обратной связи;

W_раз(p) - передаточная функция разомкнутой части звена (системы). Подставляя значение Х_oc(p) из второго уравнения системы (4.16) в пер­вое, а затем полученное выражение в третье, получим:

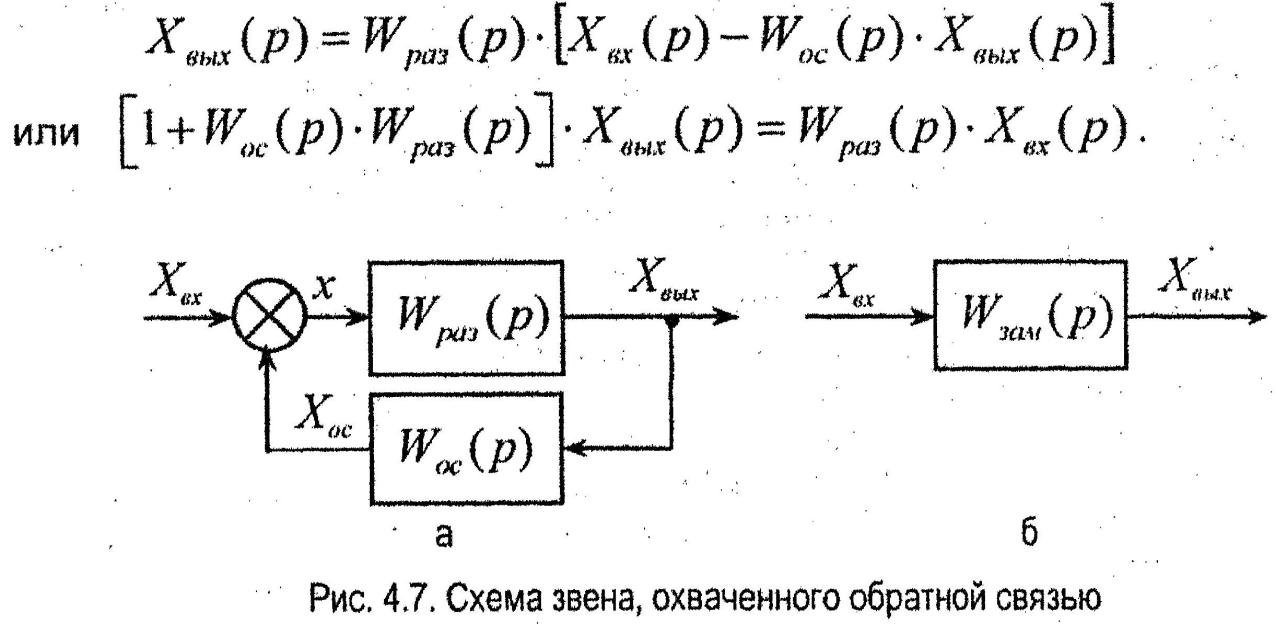
Отсюда передаточная функция замкнутой системы при отрицательной обратной связи

. (4.17)

В случае положительной обратной связи

. (4.18)

В общем случае имеем

. (4.19)

Если в схеме имеется единичная обратная связь

. (4.20)

4.4. Преобразование структурных схем

На практике системы автоматического регулирования чаще всего оказываются многоконтурными, содержащими произвольное число связанных друг с другом контуров регулирования. Передаточная функция системы в этом случае может быть найдена двумя путями:

1) путем преобразования многоконтурной системы в эквивалентную одноконтурную;

2) применением готовой формулы для передаточной функции замк­нутой системы произвольной сложности.

В основном применяется первый путь. В этом случае возникает необ­ходимость преобразования структурных схем САР и превращения их в одноконтурные. При преобразовании схем необходимо пользоваться пра­вилами преобразования. Кроме того, применяется ряд дополнительных правил преобразования, рассмотренных ниже.

1. Если структурная схема САР не имеет перекрещивающихся об­ратных связей и все элементы, входящие в структурную схему, пред­ставляют собой группы элементов с последовательным или параллель­ным соединением и с охватом их обратными связями, то передаточные функции системы определяются на основании уже рассмотренных правил.

В качестве примера рассмотрим преобразование следующей струк­турной схемы (рис. 4.8).

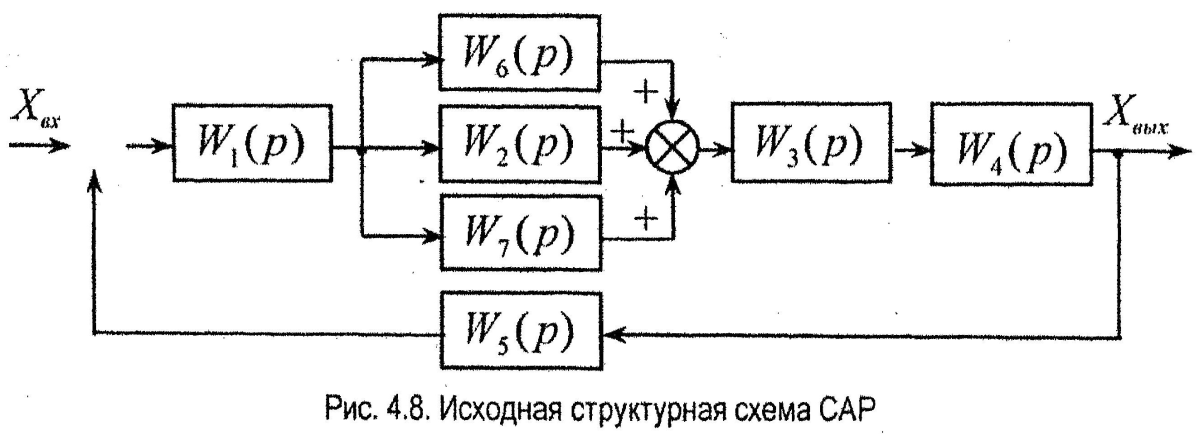
Для параллельно соединенных звеньев передаточная функция

.

В этом случае структурная схема (см, рис. 4.8) превратится в схему

(рис. 4.9.а).

Передаточная функция разомкнутой части САР

.

Передаточная функция замкнутой САР

.

2. Если структурная схема CAP имеет перекрещивающиеся парал­лельные связи, то расчёт передаточных функции систем усложняется.

Расчет передаточных функций в этих случаях можно выполнить, про­водя предварительные преобразования структурной схемы. Основной задачей преобразования многоконтурной структурной схемы является приведение ее к схеме с неперекрещивающимися связями, когда отдель­ные контуры схемы не сцепляются друг с другом. В результате исходная схема приводится к одноконтурной.

При таких преобразованиях пользуются некоторыми дополнительны­ми правилами преобразования структурных схем, которые сводятся к сле­дующему:

1. Перестановка однородных элементов и взаимная перестановка сумматоров всегда допустима, т к. от перестановки слагаемых сумма не меняется. Можно перестанавливать местами динамические звенья с постоянными параметрами (рис.4.10).

2. Перестановка сумматоров (прямое дублирование). При переносе сумматора через узел по ходу сигнала, или узла через сумматор против хода сигнала, сумматор необходимо повторить, т. е. задублировать в ответвляющейся цепи, чтобы сохранить в ней величину сигнала (рис. 4.11).

3. Перестановка узлов (рис. 4.12).

4. Передвижение сумматора с выхода элемента на его вход (рис. 4.13).

5. Передвижение сумматора со входа элемента на его выход (рис. 4.14).

6. Перенос звена через узел разветвления (рис. 4.15).

7. Правила переноса звеньев (рис.4.16).

Пример преобразования структурной схемы на рис.4.17.

;

.

Результирующая передаточная функция системы

.