
- •Глава 1. Общие сведения о системах автоматического управления и регулирования
- •1.1.Основные понятия и виды
- •1.2.Виды воздействий в системах автоматического регулирования
- •1. Единичный скачок и ступенчатое воздействие
- •2. Единичный импульс
- •3. Импульсное воздействие
- •5. Синусоидальное воздействие
- •1.3. Классификация систем автоматического
- •4.Понятие о линейных и нелинейных системах
- •5.Классификация сар в зависимости от способов их настройки
- •1.4. Контрольные вопросы для сямопроверки
- •Глава 2. Математическое описание систем автоматического управления
- •2.1.Постановка задачи
- •2.2. Математическое описание линейных сау
- •2.3. Передаточные функции сау
- •. (2.19)
- •2.4.Переходные функции( временные характеристики) элементов сау
- •2.5.Импульсная переходная(весовая)
- •2.6.Частотные характеристики сау
- •2.7. Логарифмические частотные характеристики сау
- •2.8. Контрольные вопросы для самопроверки
- •Глава 3. Типовые звенья систем
- •3.1.Разделение сау на типовые звенья
- •3.2. Безынерционное звено
- •3.3. Апериодическое звено первого порядки
- •. (3.9)
- •3.4. Колебательное звено
- •5.5. Апериодическое (инерционное) звено второго порядка
- •Временные характеристики звена
- •3.7.2. Реальные интегрирующие звенья или интегрирующие звенья с замедлением
- •3.8. Пропорционально-интегральное звено (изодромное)
- •Частотные характеристики звена (рис. 3.31)
- •Логарифмические частотные характеристики
- •3.9. Дифференцирующие звенья
- •3.9.1 Идеальное дифференцирующее звено
- •3.9.2. Реальное дифференцирующее звено
- •3.10.Пропорционально-дифференцирующее звено
- •Частотные характеристики пд-звена
- •3.11. Пропорционально-интегрально-дифференциальное звено (пид-звено)
- •Частотные характеристики
- •3.12.Запаздывающее звено
- •3.13. Особые звенья линейных сау
- •3.13.1. Устойчивые неминимально-фазовые звенья
- •3.13.2. Неустойчивые звенья
- •3.14.Контрольные вопросы для самопроверки
- •Глава 4. Структурные схемы сар и их преобрабования
- •4.1.Понятия о структурной схеме
- •4.2.Пример составления структурной схемы системы
- •4.3. Получение передаточной функции разомкнутой системы по передаточным функциям звеньев
- •4.3.1.Передаточная функция цепи последовательно соединенных звеньев направленного действия
- •4.3.2. Параллельное соединение звеньев направленного действия (рис. 4.6)
- •4.3.3.Передаточная функция системы, охваченной обратной связью
- •4.4. Преобразование структурных схем
- •4.5. Построение частотных характеристик разомкнутой системы по частотным характеристикам звеньев
- •4.6.Построение логарифмических частотных характеристик разомкнутых сар
- •4.7.Передаточные функции замкнутых сар
- •4.7.1. Передаточные функции замкнутой системы по отношению к задающему и возмущающему воздействиям
- •4.8. Контрольные вопросы для самопроверки
Частотные характеристики
АФХ:
 .
(3.100)
.
(3.100)
АЧХ:
 .
(3.101)
.
(3.101)

ФЧХ:
 .
(3.102)
.
(3.102)
ЛАЧ:
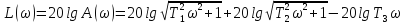 .
(3.103)
.
(3.103)
Логарифмические частотные характеристики представлены на рис.3.44.
3.12.Запаздывающее звено
Запаздывающее звено - это звено, которое на выходе воспроизводит входной сигнал без искажений, однако с некоторым постоянным запаздыванием τ (рис. 3.45).

Уравнение запаздывающего звена
 .
(3.104)
.
(3.104)
Уравнение в операторном виде
 .
(3.105)
.
(3.105)
Передаточная функция
 .
(3.106)
.
(3.106)
Амплитудно-фазовая характеристика
 .
(3.107)
.
(3.107)
 .
(3.108)
.
(3.108)
Графически АФХ может быть представлена окружностью с центром в начале координат с радиусом, равным k (рис. 3,46).
 ;
;
 ;
;
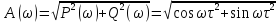 .
.

Логарифмическая
амплитудная частотная характеристика
 ,
т.е. совпадает с осью абсцисс.
,
т.е. совпадает с осью абсцисс.
3.13. Особые звенья линейных сау
Кроме типовых линейных, в САУ встречаются звенья, которые по характеристикам существенно отличаются от типовых. К таким звеньям относятся:
- неминимально-фазовые звенья, передаточные функции которых дробно-рациональны и имеют нули в правой полуплоскости;
- неустойчивые звенья, имеющие полюсы в правой полуплоскости;
- звенья с распределенными параметрами.
3.13.1. Устойчивые неминимально-фазовые звенья
В ряде устройств САР могут встречаться звенья, описываемые дифференциальными уравнениями, имеющими отрицательные коэффициенты в правой части уравнения и соответственно нули в правой полуплоскости. При этом фазовый сдвиг между входным и выходным сигналом может превышать π/2.
Дифференциальное уравнение устойчивого неминимально-фазового звена первого порядка
 .
.
Передаточная функция звена
 .
.
Комплексная частотная передаточная функция
 .
.
Частотные характеристики для данного звена представлены на рис. 3.47.

Построение выполнено для характеристик
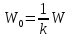
при
 .
.
Частотные годографы имеют вид полуокружностей
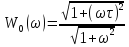 .
.
По передаточной функции могут быть найдены переходная функция (рис. 3.48, а)

и весовая функция (рис. 3.48, б).
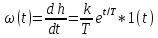 .
.

Рассмотренные типовые позиционные звенья являются устойчивыми и относятся к так называемым минимально-фазовым звеньям. Устойчивость - способность звена переходить в новое установившееся устойчивое состояние равновесия после приложения ограниченного внешнего (управляющего или возмущающего) воздействия.
Имеются неустойчивые звенья и САР, в которых после приложения ограниченного внешнего воздействия выходные координаты неограниченно возрастают или возрастает амплитуда незатухающих колебаний.
3.13.2. Неустойчивые звенья
Наиболее общая форма дифференциального уравнения неустойчивого звена первого порядка может быть записана в следующем виде:
 .
.
Передаточная функция звена
 ,
,
т.е. в отличие от устойчивого звена изменяется знак при Т.
Наиболее распространенным примером неустойчивого звена является квазиинерционное звено, описываемое следующим уравнением:
 .
.
Передаточная функция звена
 .
.
Комплексная частотная передаточная функция звена
 .
.
Частотные характеристики звена (рис. 3.49)
 ,
,
 .
.
Временные характеристики звена (рис. 3.50)
 ,
,
 .
.
Графически временные характеристики h(t) и ω(t) представлены на рис. 3.50.
Из рассмотрения полученных характеристик можно сделать вывод, что
неустойчивые
звенья могут иметь точно такие же
амплитудные частотные характеристики,
как и устойчивые, но фазовые характеристики
существенно различаются.
Следовательно, для таких звеньев имеют место большие фазовые сдвиги, чем для устойчивых звеньев, поэтому эти звенья относятся к неминимально-фазовым звеньям. Для линейных неустойчивых звеньев не существует устойчивого режима, и с течением времени при любой входной величине выходная величина стремится к бесконечности.
Колебательные неустойчивые звенья имеют следующие переходные функции:
 .
.
Они имеют незатухающий переходной процесс (рис. 3.51).

