3.7.2. Реальные интегрирующие звенья или интегрирующие звенья с замедлением

Реальные интегрирующие звенья обычно обладают опреде­лённой инерционностью, вследствие чего, их выходная величина при по­даче на вход входного сигнала изменяется с определённым замедлением.

Исходное дифференциальное уравнение интегрирующего звена с за­медлением будет иметь вид

(3.59)

или в операторном виде

,

или

.

Изображение выходной величины

. (3.60)

Если перейти от изображения к оригиналу при подаче на вход ступен­чатого воздействия X_вх=const и при нулевых начальных условиях, получим выражение переходной функции

. (3.61)

Принимая Х_вх=1, получим уравнение переходной функции, график ко­торой приведён на рис. 3.26.

Импульсная весовая переходная функция, т.е. реакция звена на еди­ничный импульс

. (3.62)

Передаточная функция имеет следующий вид:

. (3.63)

Уравнение амплитудно-фазовой характеристики

.

Если определить вещественную и мнимую части, то получим

. (3.64)

Амплитудная частотная характеристика

.

Фазовая частотная характеристика

. (3.66)

Амплитудная и фазовая частотные характеристики звена представле­ны на рис. 3.27.

ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ (РИС.3.28)

Логарифмическая амплитудная частотная характеристика

. (3.67)

3.8. Пропорционально-интегральное звено (изодромное)

Исходное дифференциальное уравнение звена

или

. (3.68)

Данное звено используется обычно в качестве регуляторов электро­приводов. Передаточная функция звена может быть получена:

;

;

;

;

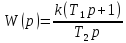. (3.69)

Следовательно, рассматриваемое звено является комбинацией про­порционального и интегрирующего звеньев.

На структурных схемах ПИ-звено изображается следующим образом (рис. 3.29).

ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ЗВЕНА (рис. 3.30)

Используя принцип наложения, переходная функция h(t) мо­жет быть получена как сумма переходных функций, пропорционального и интегрирующего звеньев, т.е.

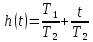. (3.70)

Весовая функция звена

. (3.71)

Для звеньев, которые содержат интегральную составляющую, при сигнале на входе равном нулю, выходной сигнал остается постоянным.

Частотные характеристики звена (рис. 3.31)

АФХ

. (3.72)

АЧХ

. (3.73)

ФЧХ

,

. (3.74)

Логарифмические частотные характеристики

ЛАЧХ

. (3.75)

Построение ЛАЧХ следует начинать с составляющей L₁(ω).

.

.

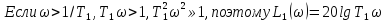Наклон этой части характеристики L₁(ω) находится следующим образом:

;

;

Следовательно, наклон характеристики L₁(ω) составляет +20 дБ/дек. Составляющая ЛАЧХ L₂(ω).

.

Если ;

,

т.е. наклон характеристики составляет -20 дБ/дек. ЛАЧХ L(ω) и её состав­ляющие L₁(ω) и L₂(ω), а также фазовая характеристика φ(ω) представле­ны на рис. 3.32.

3.9. Дифференцирующие звенья

3.9.1 Идеальное дифференцирующее звено

Идеальным дифференцирующим звеном (импульсным зве­ном первого порядка) называется звено, выходная величина которого пропорциональна скорости изменения входной величины.

, (3.76)

где k=Т, Т - коэффициент передачи (постоянная величина), имеет раз­мерность [с].

Примером дифференцирующих звеньев могут служить: гидравличе­ский успокоитель с пружиной, трансформатор, цепь RC, цепь RL, и т.д. Идеальными дифференцирующими звеньями можно считать все рассмот­ренные выше устройства, если в них пренебречь электрическими сопро­тивлениями и силами трения (в механических устройствах).

Операторное уравнение звена

.

Передаточная функция звена

. (3.77)

Графически дифференцирующее звено изображается следующим образом.

ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ЗВЕНА (рис. 3.33)

Переходная функция звена может быть получена непосред­ственно из уравнения (3.73).

Переходная функция или изменение выходной величины при подаче на вход ступенчатого воздействия может быть определена исходя из сле­дующих соображений.

Ступенчатая входная функция, как разрывная, не дифференцируется, но ско­рость изменения входной ве­личины на ступени равна бес­конечности, т.к. происходит конечное изменение входной величины в отрезок времени, стремящийся к нулю. А т.к. у дифференцирующего звена выходная величина пропорциональна скорости изменения входной, то у иде­ального звена при подаче на вход ступенчатого воздействия выходная вели­чина в момент времени, равный нулю, даст всплеск до бесконечности, а за­тем обратится в нуль, т.к. скорость изменения входной величины во все по­следующие моменты равна нулю.

Переходная функция

.

Весовая функция

.

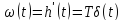ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНА (рис. 3.34)

Уравнение амплитудно-фазовой характеристики

, (3.78)

т.е.

.

Уравнения амплитудной и фазовой частотной характеристик:

, (3.79)

.

ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНА

ЛАЧХ: L(ω) = 20lgkω - это прямая, проведенная в лога­рифмическом масштабе с наклоном +20 дБ/дек и проходящая через точку с абсциссой ω=1 и ординатой 20lgk.

.

ЛАЧХ звена L(ω) получается сложением ординат слагаемых L₁ (ω) и L₂(ω) (рис. 3.35). При ω=1 L(ω)=20lgk. Частота ω_с, при которой L(ω) пересекает ось частот, находится следующим образом:

.

Отсюда .

ЛАЧХ L(ω) строится следующим образом.

Находится ω_c= 1/T, отмечается на оси частот, и через эту точку проводится прямая с наклоном +20 дБ/дек (рис. 3.36).