5.5. Апериодическое (инерционное) звено второго порядка

Исходное дифференциальное уравнение

.

Примерами этих звеньев являются двигатель постоянного тока, если на вход его подают напряжение, а выходом является его скорость; цепоч­ка R-L-C; генератор постоянного тока.

Операторное уравнение

.

Передаточная функция

.

Апериодическое звено 2-го порядка будет иметь место при последо­вательном соединении двух апериодических звеньев первого порядка ли­бо при колебательном звене, если Т₂>2Т₁ т.к. при этом корни характери­стического уравнения вещественные.

.

В этом случае исходное дифференциальное уравнение примет вид

.

Корни характеристического уравнения

;

.

Передаточная функция звена принимает вид

.

Временные характеристики звена

Если характеристическое уравнение не имеет кратных и нуле­вых корней, переходная функция h(t) определяется с помощью обратного преобразования Лапласа. Если передаточную функцию представить в виде ,

то в соответствии с обратным преобразованием Лапласа

.

Для рассматриваемого звена i=2.

Корни характеристического уравнения

;

;

.

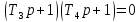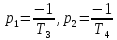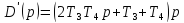Следовательно

(3.37)

или

(3.38)

При T₃>T₄.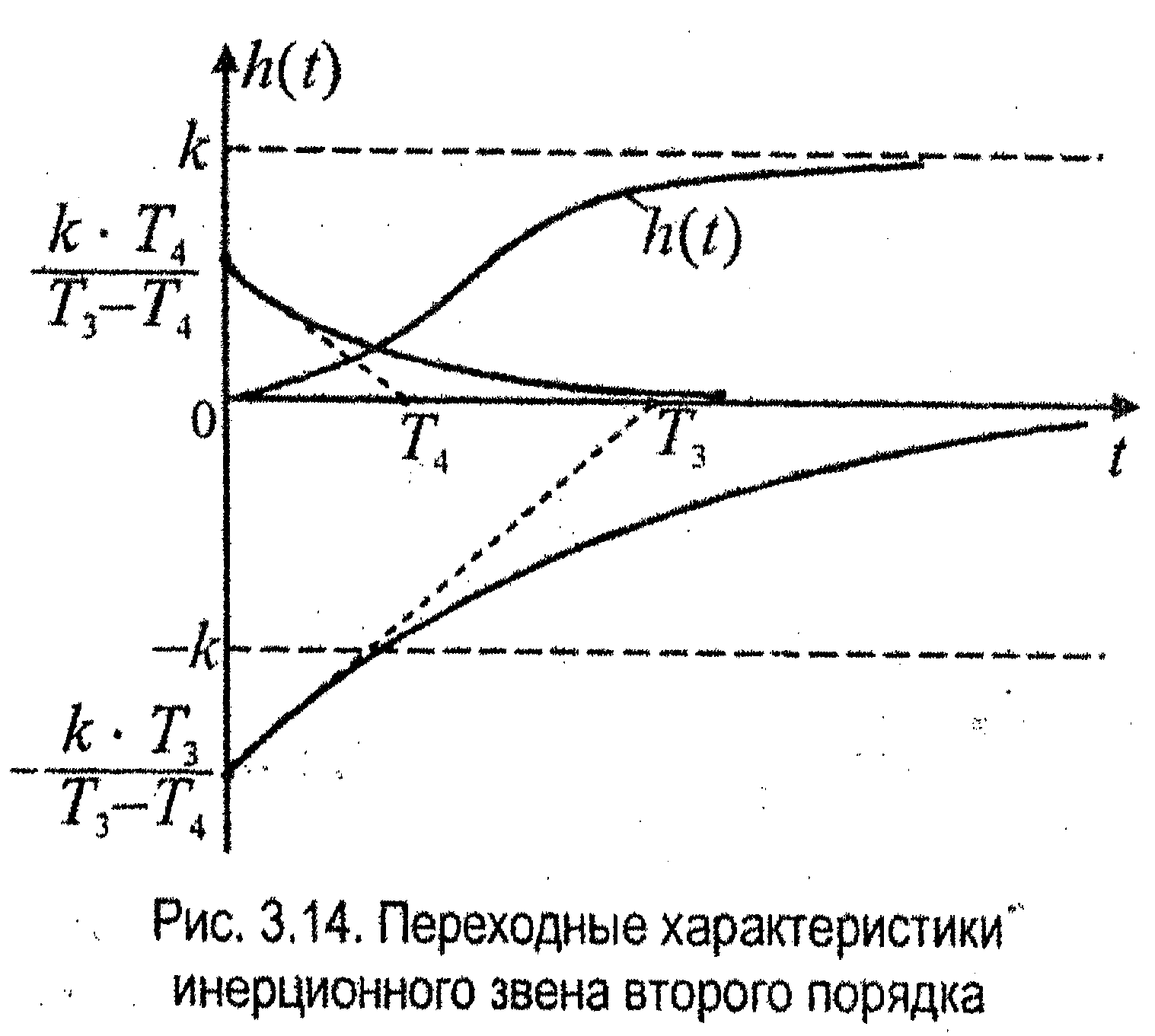

На рис. 3.14 представлены кривые переходного процесса инерционного звена 2-го порядка (его составляющие). Из графиков видно, что меньшие (малые) постоянные времени влияют на начало переходно­го процесса, а большие по­стоянные времени определя­ют среднюю часть и оконча­ние процесса.

Время переходного про­цесса (регулирования) может быть определено

.

Импульсная (весовая) пе­реходная функция (рис. 3.15)

.

ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНА

АФЧХ инерционного звена 2-го порядка имеет вид (рис. 3.16)

.

Амплитудно-частотная характеристика А(ω) (рис. 3,17).

.

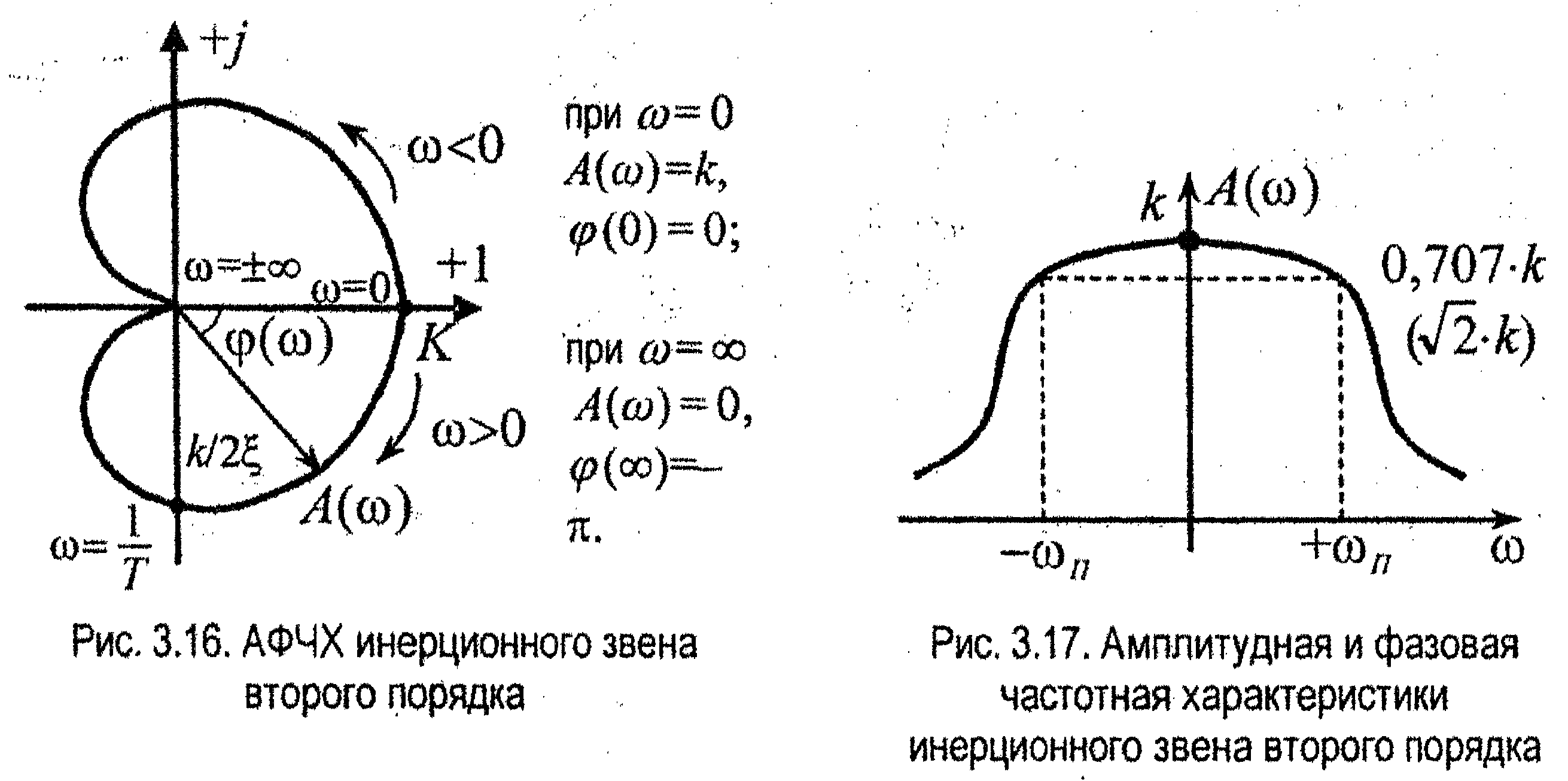
Фазочастотная характеристика φ(ω) (рис. 3.17)

.

Логарифмические амплитуды L(ω) и фазовой φ(ω) частотные харак­теристики инерционного звена второго порядка представлены на рис. 3.18.

5.6. КОНСЕРВАТИВНОЕ ЗВЕНО

Консервативное звено может быть получено из колебатель­ного звена при ξ=0. Исходным уравнением консервативного звена будет

. (3.39)

Данное звено является генератором гармонических синусоидальных колебаний.

Операторное уравнение звена

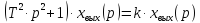. (3.40)

Передаточная функция звена

. (3.41)

Структурная схема звена.

ПЕРЕХОДНАЯ ФУНКЦИЯ ЗВЕНЯ h(t)

Характеристическое уравнение звена

.

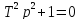Отсюда корни уравнения определяются

,

Где - угловая частота колебаний.

.

Используя обратное преобразование Лапласа, получим следующие выражения для переходной функции:

. (3.42)

.

Следовательно

. (3.43)

Или окончательно (рис. 3.19, a)

, (3.44)

где .

Весовая функция звена (рис. 3.19, б)

. (3.45)

ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНА

Частотная комплексная передаточная функция

. (3.46)

Амплитудная частотная характеристика

. (3.47)

Амплитудная и фазовая частотные характеристики звена (АФЧХ) бу­дут иметь вид (рис. 3.20):

;

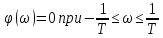; (3.48)

;

Логарифмические характеристики:

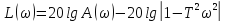; (3.49)

.

Если ,

.

Если ,

.

Суммарная ЛАЧХ консервативного звена представлена на (рис. 3.21).

3.7. ИНТЕГРИРУЮЩИЕ ЗВЕНЬЯ

3.7.1. ИДЕАЛЬНОЕ ИНТЕГРИРУЮЩЕЕ ЗВЕНО

Интегральным называется такое звено, выходная величина ко­торого пропорциональна интегралу по времени от входной величины. Звено описывается следующим дифференциальным уравнением:

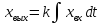
или

, (3.50)

где k - передаточный коэффициент интегрирующего звена, равный от­ношению скорости изменения выходной величины к входной. Такое звено называют также астатическим или нестабильным. Примером интегрирующего звена может служить электрический дви­гатель, если входом является скорость, а выходом - угол поворота вала, различные регуляторы САР, задающие устройства и др.

Операторное уравнение звена

.

Передаточная функция звена

, (3.51)

где k= 1/T; Т - постоянная времени интегрирующего звена.

На структурных схемах интегрирующее звено изображается следую­щим образом.

ПЕРЕХОДНАЯ ФУНКЦИЯ ИНТЕГРИРУЮЩЕГО ЗВЕНА

Если принять х_вх=1(t), то переходная функция (рис. 3.22) будет

или

.

Под постоянной времени интегрирующего звена понимают время, в те­чение которого при подаче на вход ступенчатого воздействия x_вх выходная величина достигнет этой величины.

Если входной сигнал исчезает, то выходная координата остаётся по­стоянной.

Весовая функция звена, т.е. реакция звена на единичный импульс, имеет вид

. (3.53)

ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ИНТЕГРИРУЮЩЕГО ЗВЕНА

Амплитудно-фазовая частотная функция

. (3.54)

Т.е. амплитудно-фазовая характеристика представляет собой уравнение прямой, совпадающей с отрицательным направлением мнимой оси (рис.3.23).

Уравнение вещественной и мнимой частотных характеристик будет иметь вид

.

Соответственно амплитудная и фазовая частотные характеристики определяются (рис. 3.24):

; (3.55)

; (3.56)

. (3.57)

Логарифмическая амплитудная частотная характеристика

, (3.58)

где 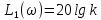- прямая, параллельная оси абсцисс;

- прямая, имею­щая наклон -20дБ/дек и проходящая через точку ω=1 на оси частот.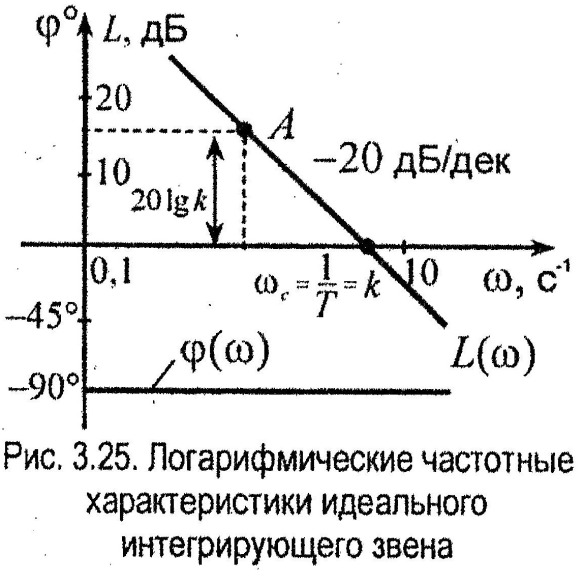

Следовательно, ЛАЧХ идеального интегрирующего звена представляет со­бой прямую, проходящую через точку с абсциссой ω= 1, ординатой 20lgk , дБ и имеющую наклон -20 дБ/дек. Логариф­мические частотные характеристики иде­ального интегрирующего звена пред­ставлены на рис. 3.25.

При изменении коэффициента k, L(ω) перемещается параллельно самой себе.