6.5. Алгебраический критерий устойчивости рауса-гурвица

Алгебраические критерии устойчивости позволяют установить, устойчива система или нет, по результатам алгебраических действий над коэффициентами характеристического уравнения. Впервые вопрос устойчи­вости динамических систем был исследован Максвеллом и Вышнеградским. В конце XIX века А. Гурвиц и Э.Дж. Раус независимо друг от друга опублико­вали работы, посвященные методу анализа устойчивости линейных систем. Критерий Рауса-Гурвица позволяет ответить на вопрос об устойчивости путём анализа характеристического уравнения системы, записанного в виде

Для ответа на поставленный вопрос необходимо установить, находит­ся ли хотя бы один из корней этого уравнения в правой половине ком­плексной плоскости.

Анализ характеристического уравнения показывает, что если все кор­ни расположены в левой полуплоскости, то все коэффициенты характери­стического полинома должны иметь один и тот же знак. Необходимо так­же, чтобы все коэффициенты были отличны от нуля (если система устой­чива). Однако эти условия являются лишь необходимыми, но не достаточ­ными. Это означает, что если данные условия не выполняются, то сразу можно сказать, что система неустойчива; но если даже эти условия выполняются, то для ответа на вопрос об устойчивости системы необходимы дальнейшие исследования.

Критерий Рауса-Гурвица даёт необходимое и достаточное условие ус­тойчивости линейных систем. Первоначально он был предложен в форме определителей, в соответствии с которыми для получения отрицательных, вещественной части, всех корней характеристического уравнения r-й степе­ни, необходимо и достаточно, чтобы при α₀>0 все n-определителей Гурвица были положительными, а затем в более удобной табличной форме.

С помощью критерия устойчивости Гурвица сравнительно просто иссле­довать устойчивость систем, описываемых уравнениями не выше 4-5-го по­рядков. Исследование же систем более высокого порядка с помощью крите­рия Гурвица становится сложным. Кроме того, недостатком этого критерия является то, что трудно проследить, как влияет тот или иной параметр системы (T, ξ, k) на устойчивость. Поэтому, наряду с алгебраическим критерием устойчивости Гурвица, применяются частотные критерии устойчивости.

В настоящее время применение алгебраических критериев не акту­ально. Ознакомиться подробнее с этими критериями можно в любом учебнике по ТАУ.

6.3.Частотный критерий устойчивости найквиста

Критерий устойчивости Найквиста, основанный на использо­вании частотных характеристик, позволяет судить об устойчивости замк­нутой САР по её амплитудно-фазовой характеристике в разомкнутом со­стоянии. Критерий был предложен Найквистом в 1932 году.

АФХ систем могут быть получены по передаточным функциям состав­ляющих её звеньев. Следовательно, если имеются структурная схема САР и передаточные функции типовых звеньев, из которых состоит эта система, то можно получить передаточную функцию разомкнутой систе­мы. Заменяя в этой передаточной функции оператор p на ϳω, получим выражение АФХ разомкнутой системы, по которому может быть построена АФХ на комплексной плоскости.

Амплитудно-фазовый критерий устойчивости формулируется сле­дующим образом.

Если АФХ разомкнутой устойчивой системы не охватывает точку с координатами (-1,ϳ0) на комплексной плоскости, то замкнутая система устойчива.

Амплитудно-фазовый критерий в такой формулировке справедлив лишь тогда, когда разомкнутая система устойчива, а в уравнении АФХ степень полинома числителя меньше степени полинома знаменателя.

Физическое толкование амплитудно-фазового критерия можно объяс­нить на примере одноконтурной системы (рис. 6.8).

В точке пересечения АФХ с отрицательной вещественной осью фазовый сдвиг между входным и выходным сигналом составляет φ=-π. В точке с координатами (-1,j0) отношение амплитуды выходного сигнала к ам­плитуде входного сигнала

т.е. колебания на выходе системы находятся в противофазе с колебаниями на входе, поэтому отрицательная обратная связь превращается в положи­тельную. В системе возникают незатухающие колебания при снятии входно­го сигнала, т.е. система будет находиться на границе устойчивости.

Если точка пересечения АФХ с вещественной осью находится между -∞ и (-1,j0), это значит, что отношение выходной амплитуды k входной больше 1, т.е. коэффициент усиления системы при данной частоте больше единицы. При подаче на вход возмущающего сигнала амплитуда выходного сигнала будет больше амплитуды входного сигнала. При замыкании такой системы в ней будут происходить свободные колебания с возрастающей амплитудой и с частотой, соответствующей точке пересечения характеристики с вещест­венной осью.

Если точка пересечения АФХ с вещественной осью находится между на­чалом координат и точкой (-1,j0), то коэффициент усиления системы при этой частоте меньше единицы и при замыкании системы свободные колебания в ней будут затухать. В многоконтурных системах формулировка и физическое толкование амплитудно-фазового критерия устойчивости усложняются.

Рассмотрим другой случай, когда АФХ разомкнутой устойчивой систе­мы имеет вид, представленный на рис. 6.9.

Если коэффициент усилений мал, то точка с координатами (-1,j0) займёт положение точки A₁ (система устойчивая). При увеличении коэф­фициента усиления k_y точка (-1,j0) перемещается вправо:

точка A₂ - система на границе устойчивости;

точка A₃ –система неустойчивая;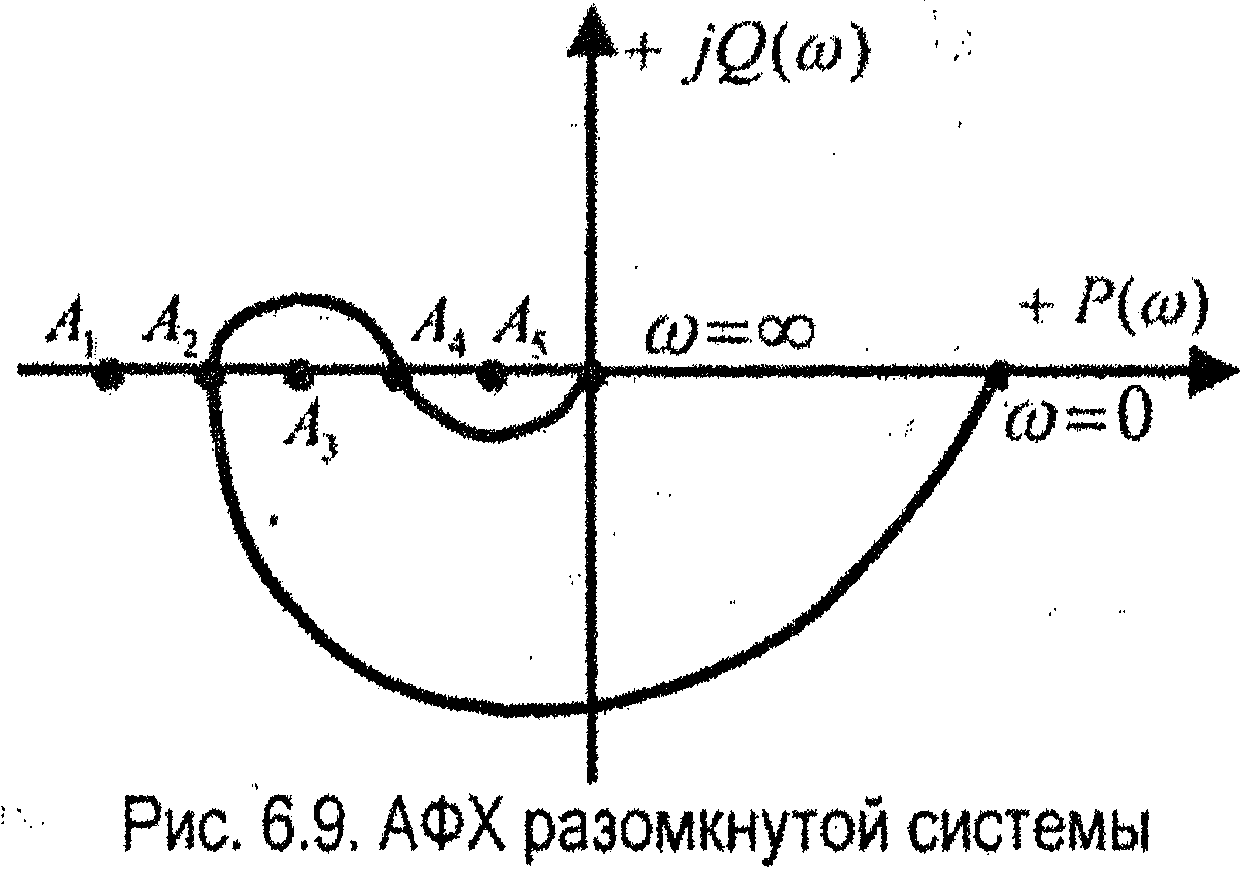

точка A₄ - система на границе устойчивости;

точка А₅ - система устойчивая.

Рассмотренная выше формули­ровка критерия Найквиста относится к системам, которые являются устойчи­выми в разомкнутом состоянии. В слу­чае одноконтурной системы устойчи­вость в разомкнутом состоянии всегда обеспечивается, если система состоит только из устойчивых звеньев (апериодических, устойчивых колебательных) и включает не более одного интег­рирующего звена. При наличии местных обратных связей должна быть ещё проверена устойчивость образованных этими связями контуров. Для этого, в свою очередь, может быть применен критерий Найквиста или любой другой.

Определить, охватывает ли АФХ точку с координатами (-1,j0), можно следующим образом. Из точки (-1,j0) проводится вспомогательный вектор AB к АФХ (рис. 6,10). При изменении ω от 0 до +∞, конец B этого вектора сколь­зит по АФХ, а вектор AB поворачивается вокруг точки A на некоторый угол. Если суммарный угол поворота вектора AB при изменении ω от 0 до +∞ ра­вен нулю, то характеристика не охватывает точку A (-1,j0) и система устой­чива (рис. 6.10, а). Если этот угол поворота не равен нулю, то характеристика охватывает точку A (-1,j0) и система неустойчива (рис. 6.10,б).

Передаточная функция астатических систем из-за наличия интегри­рующего звена имеет множитель 1/p, а в уравнении АФХ появляется соот­ветственно множитель 1/ϳω. При ω→0 АФХ разомкнутой системы уходит в бесконечность (кривая 0N₁M₁) (рис. 6.11).

Чтобы судить, охватывает ли эта кривая точку A (-1,j0), строят вспо­могательную кривую 0N₁N₂, являющуюся зеркальным отображением АФХ, и проводят дугу бесконечно большого радиуса с центром в начале коор­динат, соединяя характеристику 0N₁N₂ с характеристикой 0N₁M₁. Если те­перь обойти концом вектора AB по полученной замкнутой кривой, то сум­марный угол поворота его вокруг точки A определяет, устойчива или нет

замкнутая система. Если этот угол равен нулю (см. рис. 6.11, а), то система устойчива. Если суммарный угол поворота AB равен 4π, то замкнутая сис­тема неустойчива (см. рис. 6.11,6).

При увеличении коэффициента усиления k разомкнутой системы, АФХ, не меняя своей формы, «расширяется», т.е. расстояние каждой точ­ки характеристики от начала координат увеличивается в одинаковое число раз. Это свойство АФХ даёт возможность в некоторых сложных случаях правильно выбрать параметры системы, что трудно сделать с помощью других критериев устойчивости.

Если уменьшать коэффициент усиления в неустойчивой системе, её АФХ «сожмётся» к началу координат и система может стать устойчивой. На­оборот, при увеличении к характеристика устойчивой системы в конце кон­цов охватит точку (-1,j0) и система потеряет устойчивость (см. рис. 6.8, б).

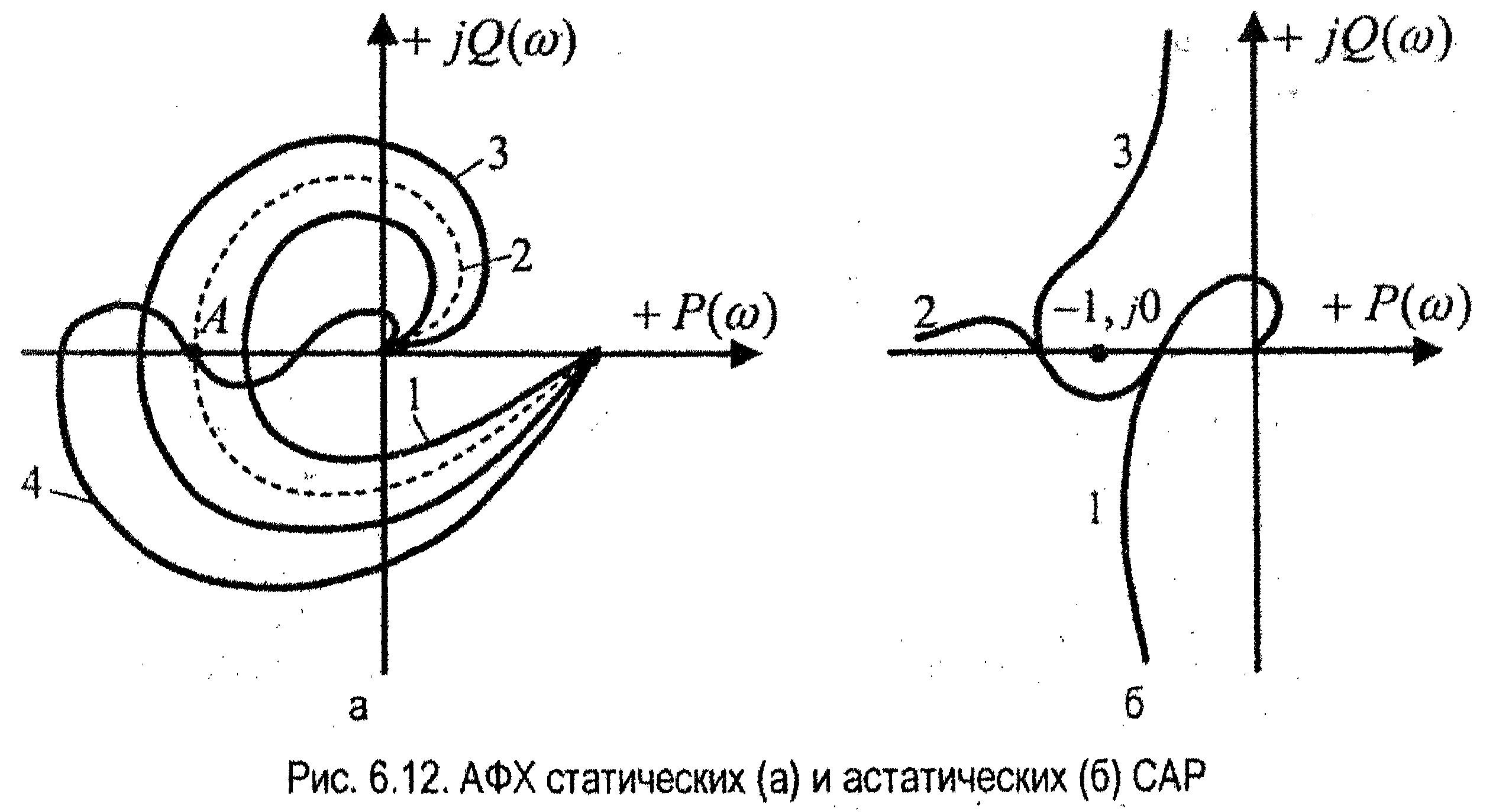
АФХ астатических систем при ω=0 уходят в бесконечность, т.к. в знаме­нателе АФХ W(ϳω) имеется множитель (ϳω)^ν, где ν- порядок астатизма.

При:

ν=1 W(ϳω) при ω=0 уходит в бесконечность отрицательной полу­оси (рис. 6.12,6);

ν=2 - вдоль отрицательной действительной полуоси;

ν=3 - вдоль положительной мнимой полуоси.

Для повышения точности в САР включают различные корректирующие устройства. АФЧХ таких систем могут иметь довольно сложную форму. Они могут пересекать вещественную ось и справа, и слева от критической точки (-1,j0) (рис. 6.14). Такие системы с «клювообразной» АФЧХ называ­ются системами «условно устойчивыми», или системами второго рода (обычные системы называются системами первого рода).

Для систем неустойчивых в разомкнутом состоянии, критерий Найкви­ста имеет следующую формулировку.

Система будет устойчива в замкнутом состоянии, если разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов АФХ через ось абсцисс слева от точки (-1,j0) равна нулю (рис. 6.14).

При анализе устойчивости системы по АФХ целесообразно ввести по­нятие запаса устойчивости по модулю и фазе (рис. 6.13).

Если через точку (-1,j0) провести окружность единичного радиуса, получим точку пересечения её с АФХ (точку B)

Запас устойчивости по модулю характеризуется отрезком h, а за­пас по фазе - углом μ.

Запас устойчивости системы по амплитуде - это величина, показы­вающая, во сколько раз необходимо увеличить (или уменьшить) величину ко­эффициента усиления системы при неизменных значениях всех остальных её параметров, чтобы устойчивая система оказалась на границе устойчивости.

Таким образом, если обозначить через k_з заданное значение переда­точного коэффициента устойчивой системы, а через k_кр - его критическое значение, т.е., такое значение передаточного коэффициента, при котором

система находится на границе устойчивости, то величина запаса устойчивости системы по амплитуде

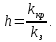
Обычно для нормальной работы требуется, чтобы h = 10÷15 дБ. При та­ком запасе изменения параметров системы, как правило, не приводят к потере устойчивости.

Запасом устойчивости системы по фазе называется величина, по­казывающая, на сколько нужно уменьшить (или увеличить) фазу системы, не изменяя её амплитуду, чтобы устойчивая прежде система оказалась на границе устойчивости

Величины запасов устойчивости в определённой мере определяют и качество САР. Обычно обеспечивается запас устойчивости по фазе μ = 30÷45. При таком значении μ возможные изменения параметров сис­темы, как правило, не приводят к потере устойчивости. Однако качество системы определяется запасами устойчивости неоднозначно. На качество системы оказывает большое влияние и форма кривой частотных характе­ристик системы.