1. Корни вещественные

Если все корни отрицательные, то стечением времени все члены уравне­ния (6,6), содержащие множитель ,стремятся к нулю, т.к.,а отклонение регулируемой величины y(t) стремится к постоянному значению у_вын(t) или к нулю. Система в этом случае устойчива.

Если хотя бы один из корней, на­пример, p₁ положителен, то соответст­вующий член с течением вре­мени неограниченно возрастает и от­клонение регулируемой величины y(t) = y_св(t)→∞. Система в этом слу­чае будет неустойчивой (рис. 6.2),

Если все вещественные корни отрицательны, то каждая составляющая или множитель стремятся к нулю приt→∞, т.е.

Если же вещественные части корней положительны (p_i>0), то

и система неустойчивая.

2. Корни комплексные сопряжённые с отрицательной веществен­ной частью

где α_i - показатель затухания колебаний;

Ω_i - круговая частота затухающих колебаний.

В этом случае

(6.7)

Если корни сопряженные ком­плексные, то в этом случае при от­рицательных вещественных частях отклонение регулируемой величины приходит к установившемуся значе­нию (к нулю) с затухающими гармо­ническими колебаниями (рис. 6.3).

Действительно, если веществен­ные части α_i всех комплексных корней отрицательны, то каждое слагаемое суммы (6.7) представляет собой затухающее колебание и поэтому

т.е. система устойчивая.

3. Корни комплексные, сопряжённые при положительной вещест­венной части

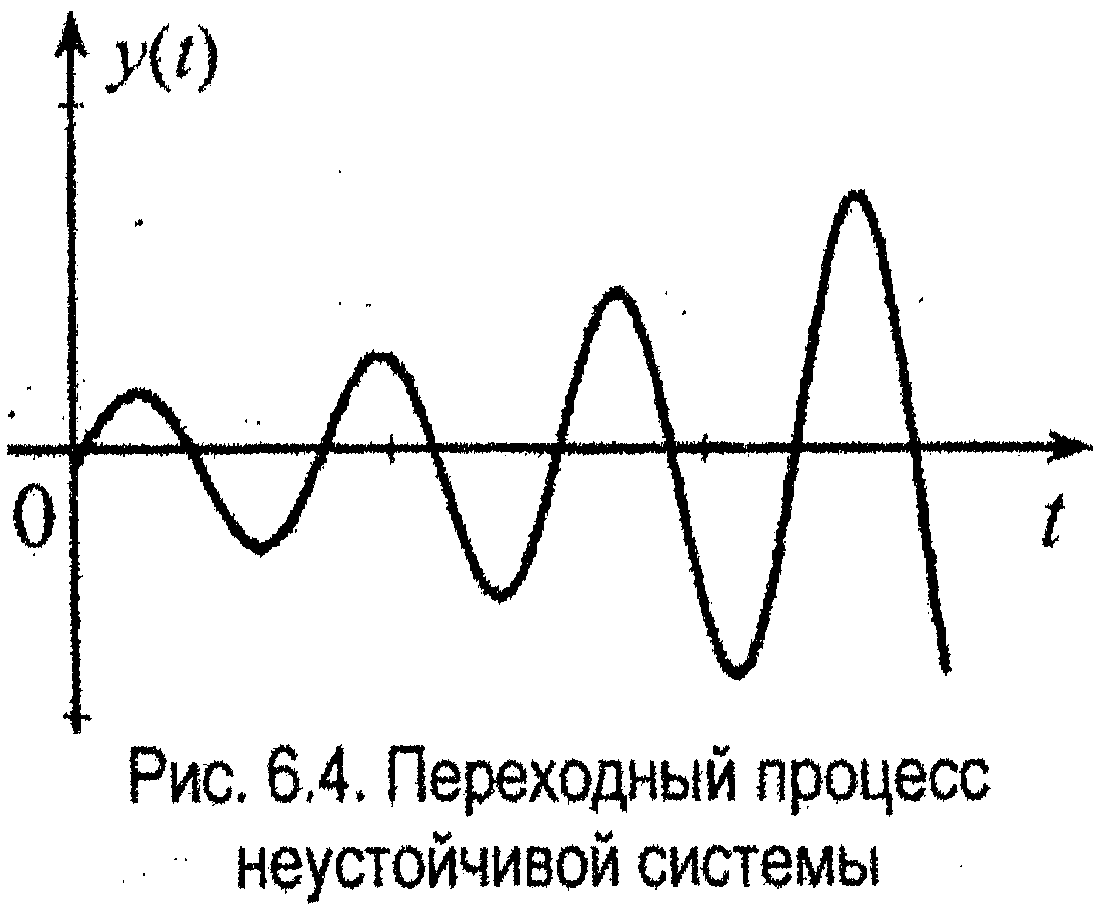
Если хотя бы одна пара комплексных корней имеет положительную веществен­ную часть (α_i > 0), то в этом случае

(6.8)

т.е. отклонение регулируемой величины совершает колебания с неограниченно возрастающей амплитудой. Система неустойчива (рис. 8.4).

4. Корни имеют нулевую вещественную часть (α_i= 0), т.е.

В этом случае отклонение регулируемой величины совершает незату­хающие колебания (автоколебания), т.е. система находится на границе устойчивости (рис. 6.5).

Система будет находиться на гра­нице устойчивости при наличии:

- нулевого корня,

- пары чисто мнимых корней,

- бесконечного корня.

Таким образом, условием устойчи­вости системы автоматического управ­ления является отрицательность вещественных частей всех корней характе­ристического уравнения (т.е. располо­жение всех корней характеристического уравнения в левой полуплоскости ком­плексной плоскости корней, рис. 6.6).

Корни характеристического уравнения замкнутой системы зависят только от параметров системы (коэффициентов уравнения), т. е. от постоянных времени и коэффициентов усиления звеньев.

Корни характеристического уравнения можно представить в виде векто­ров, расположенных в комплексной плоскости. Очевидно, что система будет устойчивой, если все корни располагаются слева от мнимой оси (рис, 6.7).

В случае, если один вещественный корень или пара комплексно со­пряженных корней располагается на мнимой оси, система оказывается на границе устой­чивости. Системы, у которых имеется одна пара мнимых корней, могут совершать неза­тухающие колебания (автоколебания). Если система имеет один нулевой корень при всех остальных корнях, расположенных левее мнимой оси, систему называют нейтрально устойчивой.

Для того, чтобы все корни оказались в левой полуплоскости, можно воздействовать на коэффициенты характеристического уравнения, которые связаны с корнями непрерывными зависимостями.

Задача определения устойчивости может быть решена различными методами. Можно определять корни характеристического уравнения и по ним устанавливать знаки вещественных частей. Но такой метод может быть использован, когда порядок характеристического уравнения ниже третьего. Уравнения более высоких степеней вообще не имеют аналити­ческого решения и могут быть решены лишь приближенно.

Но для определения устойчивости совершенно не обязательно знать значение корней. Достаточно убедиться только в отрицательности веще­ственных частей корней. Для этого можно воспользоваться методами, основанными на использовании критериев устойчивости.

Критерием устойчивости называется косвенный метод определения знаков вещественной части корней характеристического уравнения, не требующий решения этого уравнения.

Все известные критерии делятся на 2 группы:

1) алгебраические,

2) частотные,

К алгебраическим относятся критерии: Вышнеградского, Рауса-Гурвица. К частотным относятся критерии Михайлова, Найквиста, логарифмический критерий устойчивости. Особое место занимает выделение областей устойчи­вости. Применение того или иного критерия зависит от конкретных условий.