5.3.2. Устранение статистического отклонения введением компенсирующего воздействия

Рассматриваемый путь устранения статического отклонения заключается в обращении в нуль числителя выражения (5.7) при p=0.

т.е. в получении W_fy(0) = 0.

Такой результат может быть получен, если использовать управление по возмущению. Суть способа заключается в том, что сигнал, пропорцио­нальный измеренному внешнему возмущению, подаётся на управляющее устройство, которое осуществляет такое воздействие на объект управле­ния, чтобы компенсировать естественное влияние данного возмущения на выходную регулируемую величину объекта.

Схема системы компенсации возмущений показана на рис. 5.2.

В соответствии со схемой разомкнутой СAP (рис. 5.2, а), условие ком­пенсации возмущений F_ст на статическое отклонение у_ст будет иметь следующий вид:

(5.11)

Из этого выражения может быть найден коэффициент передачи управляющего устройства по возмущению

(5.12)

Следовательно, этот коэффициент зависит от параметров объекта управления. Последнее выражение (5.12) определяет коэффициент пере­дачи управляющего устройства УУ в зависимости от параметров объекта управления ОУ, при котором у_ст не зависит от F_ст.

На рис. 5.2, б изображена комбинированная САУ. В ней замкнутая САУ, рассмотренная ранее, дополнена разомкнутой системой компенсации возмущения F_ст на у_ст. В этой системе

(5.13)

где

При выполнении условия (5.12) W_fy(0)= 0, поэтому с точки зрения

статики замкнутая система освобождена от влияния возмущения F.

Компенсация может быть также применена к возмущениям, дейст­вующим не только на объект управления, но и на любое звено управляю­щего устройства. Компенсация возмущений не делает систему астатиче­ской, т.к. другие, не скомпенсированные, возмущения по-прежнему созда­ют статическое отклонение у_ст. Однако такая компенсация позволяет рез­ко снизить суммарное статическое отклонение у_cт, вызванное всеми воз­мущениями, которое определится формулой

(5.14)

В этом случае из числителя этого выражения исключается одно из слагаемых. Величина статического отклонения при этом может быть сни­жена на порядок, если компенсация осуществляется по наиболее сильно влияющему на у_ст возмущению.

5.4. ДИНАМИЧЕСКИЕ СТАЦИОНАРНЫЕ РЕЖИМЫ САУ

Как было рассмотрено выше, стационарные (установившие­ся) режимы в САУ возникают в результате приложения к ним внешних воздействий, изменяющихся во времени по определённому установивше­муся закону. Типовыми воздействиями такого рода являются гармониче­ские воздействия и воздействия, изменяющиеся с постоянной производ­ной - скоростью или ускорением. Рассмотрим эти режимы.

5.4.1. СТАЦИОНАРНЫЙ РЕЖИМ САУ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТИИ

В этом режиме при передаче на вход внешнего гармонического воздействия выходная величина системы у приходит в вынужденное колеба­ние с частотой, равной частоте внешнего воздействия. Амплитуда и фаза колебаний y определяются известными нам частотными характеристиками замкнутой системы, т.е. в стационарном режиме, вызванном воздействием

(5.15)

выходная величина системы

(5.16)

где - амплитуда выходных колебаний системы;

- фаза выходных колебаний системы.

Таким образом, гармонический стационарный режим САУ определя­ется её частотными характеристиками, которые были рассмотрены ранее.

5.4.2.СТАЦИОНАРНЫЙ ДИНАМИЧЕСКИЙ РЕЖИМ САУ ПРИ ВОЗДЕЙСВИЯХ, ИЗМЕНЯЮЩИХСЯ С ПОСТОЯННОЙ ПРОИЗВОДНОЙ

Выше был рассмотрен вопрос определения ошибки системы в установившемся режиме при подаче на её вход задающего воздействия в виде ступенчатой функции, у которой первая и производные более вы­сокого порядка в установившемся режиме равны нулю.

Однако на практике задающее воздействие g(t) может быть самой различной функцией времени, содержащей первую производную, равную скорости изменения задающего воздействия, вторую производную, рав­ную ускорению воздействия, и производные более высокого порядка.

Например, на рис. 5.3, а представлено изменение задающего воздействия, из­меняющегося по закону

(5.17)

где g_o -начальное значение g(t);

g₁=dg/dt=const- первая производная задающего воздействия.

В общем случае задающее воздейст­вие g(t) может содержать r производных

где g₁,g₂…,g_r - начальные значения от первой до r-й производных за­дающего воздействия.

Будем считать, что воздействие изменяется с постоянной r-й производной

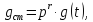
Наиболее часто в САР используются задающие воздействия, изме­няющиеся с учетом первой и второй производных, т.е.

Рассмотрим влияние формы задающего воздействия на статическую ошибку ε(t) в следящей системе, для которой

При приложении скачкообразного задающего воздействия для систе­мы, не имеющей в своем составе интегрирующих звеньев,

Если в системе имеется одно интегрирующее звено

Следовательно, следящая система с астатизмом первого порядка (имеющая одно интегрирующее звено) не имеет ошибки в установившем­ся режиме при ступенчатом задающем воздействии,

Если задающее воздействие изменяется по линейному закону g(t)=g₀+g₁∙t (первая производная),

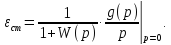
Для системы, не содержащей интегрирующего звена, либо для систе­мы, имеющей одно интегрирующее звено,

т.е. статическая ошибка . Ее называют скоростной ошибкой.

Если же система содержит два интегрирующих звена, то статиче­ская ошибка

Отсюда можно сделать следующие выводы:

1. Если порядок астатизма системы равен порядку высшей произ­водной задающего воздействия, то ошибка системы в установив­шемся режиме будет иметь определенное значение.

2. Если порядок астатизма системы ниже, чем порядок высшей про­изводной задающего воздействия, то ошибка системы с течением времени будет увеличиваться до бесконечности.

3. Если порядок астатизма системы больше, чем порядок высшей производной задающего воздействия, то ошибка системы в уста­новившемся режиме равна нулю.

Таким образом, введение в системы регулирования определенного количества интегрирующих звеньев позволяет ограничивать или совсем ликвидировать установившееся отклонение регулируемой величины y_ст, или ошибки регулирования ε_ст при наличии воздействия непрерывно из­меняющегося (постоянной производной).