7.4. Общая характеристика задач синтеза сар

Под синтезом САР понимается задача выбора и расчета па­раметров специальных, корректирующих устройств, обеспечивающих за­данные статические и динамические характеристику САУ. При этом пред­полагается, что основные функциональные элементы выбраны, объект регулирования задан. Для многих систем задача синтеза сводится к выбо­ру регулятора с требуемыми характеристиками, обеспечивающего задан­ный закон регулирования. Следовательно, при синтезе по требуемым ста­тическим и динамическим показателям определяют структурную схему САР, обеспечивающую или улучшающую эти показатели. Решение задач синтеза не однозначное, т.к. одни и те же показатели качества можно удовлетворить различными путями.

Задача синтеза САР упрощается, если задана её определенная неизме­няемая часть вместе с объектом регулирования. В этом случае задача синтеза сводится к выбору дополнительных корректирующих устройств, т.е. к их синте­зу. Следовательно, коррекцией САР называют осуществление специальных мер, делающих систему устойчивой и улучшающих качество её работы.

Существуют различные методы синтеза. Достаточно эффективными являются частотные методы, особенно использующие логарифмические частотные характеристики.

Коррекция осуществляется с помощью введения в систему специальных корректирующих звеньев с особо подобранной передаточной функцией.

Принципиально корректирующие звенья могут включаться либо последова­тельно, либо параллельно с основными звеньями САР. Таким образом, по способу включения в систему различают параллельные и последователь­ные корректирующие звенья (рис 7.6).

7.5. Параллельные корректирующие звенья – обратные связи

При параллельной коррекции динамические свойства звень­ев и САР могут быть улучшены с помощью дополнительных обратных связей вокруг отдельных частей системы с передаточной функцией W₀(p). В этом случае передаточная функция изменится

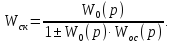
Корректирующие обратные связи могут быть отрицательные и поло­жительные, жесткие и гибкие. Жесткая обратная связь осуществляется статическим звеном, передаточная функция которой в установившемся режиме W_oc (0) = 0. Следовательно, гибкая обратная связь действует только в динамике (этим определяется её наименование).

ЖЕСТКИЕ КОРРЕКТИРУЮЩИЕ ОБРАТНЫЕ СВЯЗИ

Рассмотрим вначале действие идеальной жесткой обрат­ной связи с передаточной функцией

Пусть это обратная связь охватывает простое статическое звено пер­вого порядка (инерционное звено) с передаточной функцией

В результате такой коррекции передаточная функция звена примет вид

где -коэффициент передачи скорректированного звена;

– постоянная времени скорректированного звена.

Таким образом, охват статического звена жесткой обратной связью изменяет его постоянную времени и коэффициент усиления: т.е. уменьшает их при отрицательной обратной связи и увеличивает при положи­тельной обратной связи (рис. 7.7).

В качестве корректирующей об­ратной связи применяется в основном отрицательная обратная связь, умень­шающая инерционность звена. Кроме того, отрицательная обратная связь имеет и другие достоинства:

а) уменьшает нелинейность стати­ческой характеристики звена, неста­бильность его параметров во времени;

б) при наличии шумов (помех) на входе или внутри звена уменьшает уровень шумов на выходе.

Влияние положительной обратной связи противоположно в отношении

всех факторов.

Инерционное звено второго порядка - колебательное звено с пе­редаточной функцией

При охвате жесткой обратной связью получаем следующую переда­точную функцию:

где

При этом коэффициент, определяющий колебательность данного зве­на (коэффициент затухания), определится

т.е. при отрицательной обратной связи этот коэффициент снижается, что приводит к увеличению его колебательности. Если ξ> 1,0, то это полезно. В случае же ξ<1,0 - нежелательно.

Интегрирующее звено с передаточной функцией W₀=k₀/p при охвате жесткой обратной связью получает следующую передаточную функцию

где - коэффициент усиления скорректированного звена;

- постоянная времени скорректированного звена.

Это очень важный результат.

При охвате интегрирующего звена жесткой отрицательной связью, оно превращается в статическое (инерционное) звено.

При положительной обратной связи получается неустойчивое звено. От­рицательная обратная связь широко применяется для снижения порядка астатизма системы и соответственно для улучшения устойчивости и качества пе­реходных процессов в тех случаях, когда у системы высокий порядок астатизма. На рис. 7.8 представлены кривые переход­ных процессов для этих звеньев.

Здесь:

h₀(t) - характеристика звена без обрат­ной связи;

h(t) - характеристика звена при наличии обратной связи.

В последнем случае происходит замедление роста выходного сигнала из-за уменьшения входного сигнала .

В установившемся режиме h(ω) = 1/k_ос.

Инерционная жесткая обратная связь с передаточной функцией

охватывает статическое звено первого порядка с передаточной функцией

В этом случае передаточная функция скорректированного звена будет

где - постоянная времени скорректированного звена;

- коэффициент передачи скорректированного звена.

Следовательно, при этом порядок знаменателя передаточной функ­ции повышается на единицу. Кроме того, при отрицательной обратной связи снижается постоянная времени (эквивалентная) звена, что приводит к увеличению её быстродействия. При этом замедляется рост сигнала Х_oc. В передаточной функции скорректированного звена появляется дополни­тельное форсирующее воздействие по производной (пропорционально-дифференцирующее звено).

Инерционная положительная обратная связь замедляет переходный процесс.