Глава 5. Стационарные режимы сар

5.1. Основные понятия

Как всякая динамическая система САР может находиться в двух состояниях: стационарном (установившемся) и переходном.

Статический стационарный режим - это режим, при котором систе­ма находится в состоянии покоя вследствие того, что все внешние воз­действия и параметры самой системы не меняются во времени.

Динамический стационарный режим - это режим, возникающий тогда, когда приложенные к системе внешние воздействия изменяются по какому-либо установившемуся закону, в результате чего система приходит в режим установившегося вынужденного движения.

Стационарные динамические режимы, в свою очередь, могут быть двух типов: детерминированными и случайными. При первом режиме на систему действует детерминированное (регулярное) стационарное воздействие. В качестве примера можно назвать установившийся гармо­нический режим, описываемый частотными характеристиками.

Второй режим - стационарный случайный является установившимся в статистическом смысле и имеет место, когда приложенные к системе воз­действия представляют собой случайные, но стационарные функции времени.

5.2. Статический режим сар

Уравнение статики САУ может быть получено по уравне­нию динамики системы по возмущающему воздействию. В качестве примера рассмотрим одноконтурную САР, структурная схема которой представлена на рис. 5.1.

Передаточная функция замкнутой системы по возмущающему воз­действию:

(5.1)

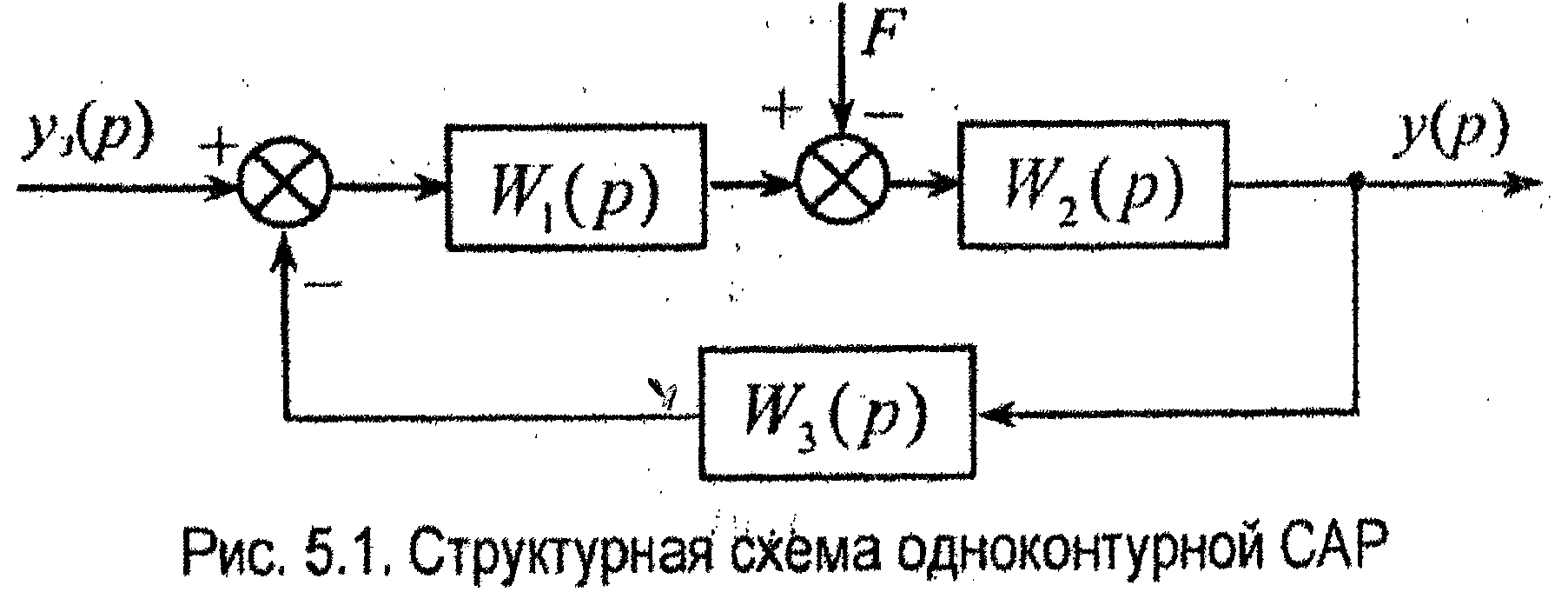
где W_fy(p) = W₂(p) - передаточная функция разомкнутой системы по возмущающему воздействию;

W(p)=W₁(p)∙W₂(p)∙W₃(p) - передаточная функция последова­тельно соединенных звеньев.

Отсюда уравнением статики будет

После окончания переходного процесса, приняв р=0, что соответству­ет постоянству всех переменных, т.е. равенству нулю всех производных, можно получить уравнение статической характеристики, т.е.

(5.2)

где у_ст - статическое приращение выходной величины САР, вызванное приращением внешнего воздействия F_сm.

Вид передаточных функций W(0) и W_fy(0) зависит от того, содержатся ли в системе интегрирующие звенья или нет.

Рассмотрим вначале систему, которая после приведения к однокон­турной системе содержит только статические звенья (инерционные и ко­лебательные). Такие системы называются статическими.

В этом случае при р=0 в выражении (5.1) будем иметь

т.к. знаменатели передаточных функций всех звеньев, входящих сомно­жителями в выражения W(p) и W_fy(p) при р=0, обращаются в единицу. Следовательно, выражение (5.2) принимает вид

(5.3)

где k - суммарный коэффициент усиления разомкнутой системы, равный произведению коэффициентов усиления всех звеньев,

k_fy - коэффициент усиления прямого канала регулирования по воз­мущению (от места приложения возмущения до места нахождения выходной величины),

Следовательно, величина k_fy определяет статическую зависимость между F и y при разомкнутом контуре системы, т.е. при отсутствии управ­ления. Статическое отклонение выходной величины при возмущающем воздействии F_cm определится

(5.4)

Сравнивав (5.3) и (5.4), можно заметить, что замыкание системы ав­томатического управления приводит к уменьшению статической зависи­мости у от F в (1+k) раз. Таким образом, для уменьшения этой зависимо­сти необходимо увеличить коэффициент передачи системы k.

Из выражения (5.2) можно найти величину статического отклонения, приходящуюся на единицу воздействия F, т. е.

(5.5)

Эта величина является мерой статической точности системы регулиро­вания и называется статизмом. Статизм иногда обозначается через S.

Для следящей системы, статическая ошибка слежения найдётся из выражения для передаточной функции системы по ошибке.

Для установившегося режима (р=0) статическая ошибка ε_ст определится

Таким образом, охват звена или системы отрицательной обратной связью увеличивает стабильность системы.

Если в системе действует несколько воздействий, то суммарное стати­ческое отклонение может быть определено с учётом этих воздействий

(5.6)

где - статизм системы по возмущениюF_стi.

Таким образом, применение замкнутой системы приводит к повыше­нию статической точности в (1+k) раз.