2.8. Метод эквивалентного генератора

В любой электрической схеме можно мысленно выделить какую-то одну ветвь, а всю остальную часть схемы условно изобразить некоторым прямоугольником, как показано на рис.22, а. По отношению к выделенной ветви вся схема, обозначенная прямоугольником, представляет собой так называемый двухполюсник.

Таким образом, двухполюсник - это обобщенное название схемы, которая двумя зажимами присоединена к выделенной ветви.

Если в двухполюснике есть источники энергии, то он называется активным (и обозначается буквой А), а если источников нет - пассивным (обозначается буквой П).

Выделим в сложной цепи одну ветвь с сопротивлением R (см. рис.22, а). Ток I в этой ветви и напряжение U на ее зажимах зависят при прочих равных условиях от величины R.

В частности, при (то есть при холостом ходе, когда ветвь аb разомкнута) ток I=0, а напряжение (индекс ‘’хх’’ обозначает холостой ход). Включим последовательно сR две э.д.с. – Е^’ и Е^’’, - равных по величине и направленных противоположно друг другу, как показано на рис.22, б.

Поскольку E`=E`` ток I от их включения в цепь не изменится. Рассчитаем теперь полученную схему методом наложения, причем в первой частичной схеме (рис.22, в) примем Е^’’=0, а во второй (рис.22, г) - все э.д.с. исходной схемы и Е^’ равными нулю,

Искомый ток равен сумме частичных токов

I=I'+I''.

Но , следовательноI'=0 и I=I''.

Вывод отсюда таков: ток в любой ветви аb электрической цени не изменится, если всю остальную цепь заменить эквивалентным генератором (активным двухполюсником), Э.Д.С. которого равна напряжению между разомкнутыми зажимами аb (то есть напряжению холостого хода), а внутреннее сопротивление - сопротивлению цепи относительно зажимов аb также при холостом ходе. Этот вывод называется теоремой об эквивалентном генераторе.

Метод эквивалентного генератора, основанный на одноименной теореме, целесообразен в тех случаях, когда требуется определить только один из токов некоторой сложной цепи.

Пусть требуется определить ток I в одной из ветвей схемы (см. рис.22, а).

Всю цепь, кроме ветви с сопротивлением R, заменим эквивалентным источником, имеющим э.д.с. и внутреннее сопротивление, как показано на рис.23.

Величинуможно определить, разомкнув зажимыab и подсчитав сопротивление цепи относительно этих зажимов (при определении э.д.с. всех содержащихся в цепи источников принимаются равными нулю. Если есть и источники тока, то ветви с ними следует считать разомкнутыми).

Из полученной неразветвленной

цепи определяем ток:

(26)

Методика применения метода:

1) находится напряжение на зажимах разомкнутой ветви ab;

2) определяется сопротивление , то есть сопротивление всей схемы по отношению к зажимамab;

3) подсчитывается искомый ток.

Пример 10.

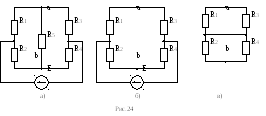
Размыкаем ветвь ab, как показано на рис.24, б, и находим :

Рассчитаем сопротивление всей схемы при закороченном источнике E относительно зажимов ab (схема рис34, в);

По формуле (26) определяем искомый ток в ветви с :

2.9. Теорема компенсации

В любой электрической цепи без изменения токораспределения в ней сопротивление можно заменить э.д.с., числено равной падению напряжения в заменяемом сопротивлении и направленной встречно току в этом сопротивлений.

Для доказательства выделим из схемы одну ветвь с сопротивлением R, по которой течет ток I, а всю остальную часть схемы представим двухполюсником, как показано на рис, 25, а.

Если в выделенную ветвь включить две равных и противопо-ложных э.д.с. Е, числено равных падению напряжения в сопротивлении R от тока I (см. рис.25, б), то ток I от этого не изменится. Определим потенциал точки с:

Но если , то точки а и с можно объединить в одну, то есть участок ас закоротить и получить схему на рис.25, в., В этой схеме вместо сопротивленияR включена э.д.с. Е.