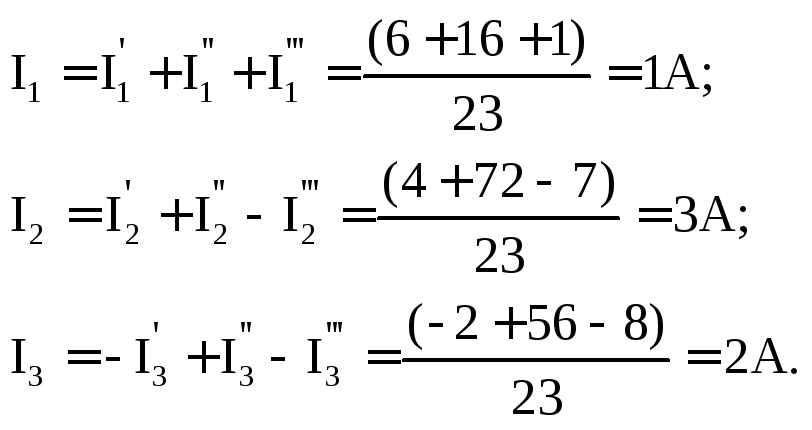2.6. Метод двух узлов

Метод двух узлов наиболее целесообразен для расчета схем с двумя узлами и непосредственно вытекает из метода узловых потенциалов. Для схемы с параллельными ветвями на рис.14 согласно формуле (18) можно записать:

С учетом принятых на рис.14 обозначений последнее соотношение перепишем для частного случая отсутствия источников тока:

(20)

П

(21)

осле определениянаходятся токи в ветвях по уже известной формуле:

Пример 7.

Три генератора с э.д.с. и внутренними сопротивлениямиработают параллельно на общую нагрузку, как показано на рис.15

Требуется определить напряжение на нагрузке , токи нагрузки и генераторов.

По формуле (20) определяем напряжение на нагрузке:

По формуле (21) вычисляем искомые токи:

2.7. Метод наложения. Преобразование схем

Ток в любой ветви линейной электрической цепи можно рассматривать как алгебраическую сумму частичных токов, вызываемых в этой ветви каждым из источников в отдельности. Это положение называется принципом наложения или принципом суперпозиции, а основанный на этом положении метод - методом наложения. Для расчета этим методом цепи необходимо:

1) произвольно расставить направления действительных токов;

2) составить частичные схемы замещения, оставив в каждой по одному источнику. Внутренние же сопротивления исключенных источников должны оставаться во всех частичных схемах;

3) рассчитав каждую схему, найти частичные токи во всех ветвях;

4) определить действительные токи как алгебраическую сумму соответствующих частичных токов.

Примечание: методом наложения нельзя пользоваться для подсчета выделяемых в сопротивлениях мощностей, т.к. мощность пропорциональна квадрату тока.

При расчете частичных схем возникает необходимость определения эквивалентного сопротивления отдельных участков схем и токораспределения в ветвях схемы.

Наиболее часто используется последовательное либо параллельное соединение резисторов и их комбинации - смешанное соединение. Для определения эквивалентного параметра при последовательном соединении суммируются сопротивления, а при параллельном – проводимости. В частном случае параллельного соединения двух резисторов, как показано на рис.16, получим эквивалентное сопротивление:

(22)

При параллельном соединении нагрузок токи в них распределяются прямо пропорционально проводимостям. Поэтому для двух параллельных нагрузок токи в каждой из них определяются через ток I в неразветвленной части цепи (см. рис.16) следующими соотношениями:

(23)

Однако встречаются и схемы, которые нельзя разбить на участки с последовательным или параллельным соединением. Примеры такого соединения нагрузок представлены на рис.17.

Схема на рис. 17, а называется треугольником, а на рис.17, б - звездой. Для удобства расчетов в зависимости от общей конфигурации схемы (относительно зажимов а, b, с которой и представлены схемы треугольника и звезды) указанные типовые соединения требуется взаимно преобразовывать.

Для эквивалентности схем необходимо и достаточно, чтобы сопротивления или проводимости между любой парой зажимов (аb, bс, са) при соединении звездой и треугольником были одинаковы. На основании этого условия разработаны формулы эквивалентного преобразования, которые приводятся ниже без вывода.

Преобразование треугольника в эквивалентную звезду:

(24)

В частном случае, если в треугольнике все сопротивления одинаковы и равны , то.

Преобразование звезды в эквивалентный треугольник:

(25)

Если в звезде все сопротивления одинаковы и равны , то.

Пример 8.

Требуется определить ток , протекающий через источник э.д.с.

Относительно узлов 1,2,3 резисторы образуют звезду. Преобразуем её в эквивалентный треугольник, состоящий из резисторови, как показано на рис.19.

E

E

Так как в звезде , то сопротивления резисторов треугольника составят значения

.

На схеме (рис.19) резисторы и, также какивключены параллельно. Заменим эти две пары резисторов эквивалентными резисторамии, воспользовавшись формулой (22):

С учетом этого схема преобразуется к виду, показанному на рис.20.

Эквивалентное сопротивление всей схемы R будет равно:

Искомый ток, согласно закону Ома

Пример 9.

Методом наложения рассчитать токи в ветвях схемы на рис.21, а если задано:

Произвольно примем направления истинных токов в ветвях (см. рис.21, а) и составим частичные схемы замещения для каждого из источников э.д.c., как показано на рис.21, б - г.

Определим эквивалентное сопротивление схемы для источника э.д,с.и частичные токи в первой схеме замещения (см. рис.21, б):

Аналогичные вычисления проведем и для двух оставшихся частичных схем замещения:

Подсчитаем истинные токи в ветвях: