2.2. Закон Ома для цепи с э.Д.С.

Рассмотрим простейшую схему на рис.4.

Потенциал точки 3 больше потен-циала точки 2 на величину э.д.с.:

(4)

Ток во внешнем участке цепи (по отношению к источнику) направлен от точки с высшим потенциалом к точке с низшим потенциалом, поэтомуна величину падения напряжения на:

(5)

Приравняем правые части равенств (4) и (5):

Из последнего уравнения получим

(6)

Следует заметить, что в формуле (6) величина отрицательная, так как

Аналогично можно определить ток для любого сложного участка цепи, например, по схеме на рис.5.

Пусть заданы все э.д.с., сопротивления и разность потенциалов между точками а и b.

Ток может иметь любое направление. Зададим условно направление стрелкой. При таком направлении тока меньшена величинуи поэтому

Из этого равенства следует

(7)

где - суммарное сопротивление участка схемы;

напряжение между выводами рассматриваемого участка, взятое по выбранному направлению тока;

- алгебраическая сумма э.д.с. (если направление э.д.с. совпадает с выбранным направлением тока, то эта э.д.с. берется со знаком "плюс", а в противном случае - со знаком "минус").

Формула (7) представляет собой закон Ома для участка цепи с э.д.с. (обобщенный закон Ома).

Если в результате расчета значение тока получилось со знаком "минус", то это значит, что действительное направление тока противоположно ранее принятому.

На участках схемы с пассивными элементами направление тока и напряжения будем всегда выбирать совпадающими.

Пример 1.

Для схемы на рис.6 задано:

Определим напряжение между точками, а и b.

Задавшись направлениемI, получим для одноконтурной замкнутой цепи

Искомое напряжение можно определить по обобщенному закону Ома, примененному к участку amb:

откуда

Применим закон Ома к участку anb:

.

Но так как , то.

Проанализировав этот простейший пример, можно сделать замечание, которое будем использовать в дальнейшем.

Замечание. Если на участке цепи, содержащем э.д.с. и сопротивление, ток и э.д.с совпадают по направлению, то напряжение па зажимах участка меньше э.д.с. на величину падения напряжения на сопротивлении, а если направление тока противоположно направлению э.д.с., то напряжение на зажимах участка больше э.д.с. на величину падения напряжения на сопротивлении.

Пример 2

К зажимам а и с схемы подключен вольтметр, как показано на рис.7 (здесь и далее внутреннее сопротивление вольтметра будем полагать бесконечно большим, следовательно, подключение или отключение вольтметра на режим работы цепи не влияет).

Если токI=10 А течет от а к с, то показание вольтметра , а если тот же по величине ток течет от с к а, то показание вольтметра

Определить величину R и E.

На основании формулы (7) при первом направлении тока

При противоположном направлении тока

.

Решим совместно два уравнения:

2.3. Законы Кирхгофа

Для сложной разветвленной цепи введем понятия ветви и узла. Ветвью цепи (или схемы) называется ее участок, состоящий только из последовательно соединенных элементов, по которым протекает один и тот же ток. Узлом называется точка соединения трех и более ветвей.

При обходе схемы по соединенным в узлах ветвям можно получить замкнутые контуры.

Законы Кирхгофа формулируются следующим образом.

Первый закон Кирхгофа - сумма подтекающих к любому узлу токов равна сумме утекающих от узла токов (физический смысл закона: заряды в узлах не скапливаются).

Второй закон Кирхгофа - алгебраическая сумма э.д.с. замкнутого контура равна алгебраической сумме падений напряжений в нем:

В этом уравнении положительные знаки принимаются для тех токов и э.д.с., положительные направления которых совпадают с произвольно выбранным направлением обхода рассматриваемого контура.

Перед составлением уравнений необходимо:

а) произвольно выбрать положительные направления токов в ветвях (и соответствующие им направления напряжений);

б) выбрать положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа,

Для примера используем схему на рис.8, содержащую шесть ветвей и четыре узла

Уравнения оп первому закону Кирхгофа:

_{Из этих уравнений независимы только три, четвертое является их алгебраическим следствием. Так, сложив уравнения (8), (9) и (10), получим уравнение (11).}

_{Таким образом, при составлении уравнений электрического равновесия в цепи по первому закону Кирхгофа необходимо составить n} .

_{Количество неизвестных в схеме (токов в ветвях) равно количеству ветвей. Поэтому по второму закону Кирхгофа следует составить m}

_{Для выбранного примера m=6-3=3.}

_{Для того, чтобы все уравнения, составленные по второму закону, были независимыми, контуры выбираются так, чтобы в каждый из них входила ветвь, не вошедшая во все остальные.}

_{Уравнения по второму закону Кирхгофа (стрелками около сопротивлений на схеме указаны направления падений напряжения):}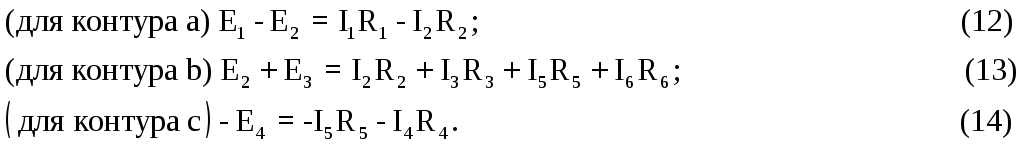

Совместное решение уравнений (8), (9), (10), (12), (13) и (14) позволит найти все токи.

Если бы в схеме были источники тока, то в ветвях с ними токи были бы определены и количество уравнений, составляемых по второму закону, уменьшилось бы на количество источников тока (при составлении уравнений при этом следовало бы выбирать независимые контуры, не содержащие источников тока).

Недостаток рассмотренного метода - его громоздкость.

Пример 3.

Для схемы на рис.9 задано:

Требуется найти токи в ветвях схемы и произвести проверку решения расчетом баланса мощностей.

Произвольно выбираем направления токов, как показано на схеме, и направления обхода контуров по часовой стрелке.

В схеме два узла, три ветви, источников тока нет. Поэтому следует составить одно уравнение по первому и два уравнения по второму законам Кирхгофа:

П

(а)

одставляем численные значения величин и решаем систему уравнений:

(б)

Подставляем в уравнение (б) значение из уравнения (а):

Окончательно получаем: Истинное направление токовипротивоположно первоначально принятому. Рассчитаем баланс мощности.

По закону сохранения энергии мощность всех источников, имеющихся в цепи, должна быть равна сумме мощностей всех включенных в эту цепь приемников и тех потерь мощности, которые выделяются внутренними сопротивлениями реальных источников. Составленное в соответствии с этим законом математическое уравнение называется балансом мощности цепи (при этом следует учитывать, что если через какой-то источник э.д.с. ток реально протекает навстречу направлению э.д.с., то такой источник является потребителем и его мощность при составлении баланса учитывается со знаком "минус”).

Мощности, доставляемые источниками в цепь:

Сумма мощностей нагрузок:

Баланс мощностей подтверждает правильность определения токов.

Пример 4.

;

Требуется определить все токи и проверить баланс мощности.

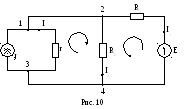
Цепь содержит четыре ветви, два узла (точки 1 и 2 на схеме образуют один узел, точки 3 и 4 - второй) и один источник тока. Поэтому следует составить одно уравнение по первому и два уравнения по второму законам Кирхгофа.

Выбранные направления обхода контуров и направления токов представлены на рисунке.

(a)

(б)

(в)

Из уравнения (в):

Из уравнения (б):

Подставляя полученные соотношения в (а), получим и остальные токи:

Напряжение на источнике тока:

Мощности, доставляемые источником тока и источником э.д.с. в цепь:

Сумма мощностей нагрузок: