5.2. Резонансные явления при несинусоидальных токах

Как известно из подраздела 3.6, резонансным режимом работы электрической цепи, содержащей одну или несколько индуктивностей и одну или несколько емкостей, называют такой режим работы ее, при котором ток на входе этой цепи совпадает по фазе с действующей на входе э.д.с.

Если воздействующая э.д.с. несинусоидальна, то в электрической цепи могут возникать резонансные режимы не только на первой гармонике, но и на высших гармониках.

Условимся под резонансом на k-й гармонике понимать такой режим работы, при котором ток k-й гармоники на входе цепи по фазе совпадает с k-й гармоникой действующей на входе э.д.с. (но притом токи остальных гармоник не совпадают по фазе с вызвавшими их э.д.с.).

При возникновении резонансного и близкого к нему режима на какой-либо высшей гармонике токи и (или) напряжения этой гармоники могут оказаться большими, чем токи и напряжения первой гармоники на тех же участках цепи, несмотря на то, что амплитуда соответствующей высшей гармоники э.д.с. на входе схемы может быть в несколько раз меньше амплитуды первой гармоники э.д.с.

Исследование резонансных явлений при несинусоидальных токах часто производят, полагая активные сопротивления дросселей нулевыми (в контурах, содержащих только конденсаторы и дроссели, но не содержащих резисторов). В таком случае входное сопротивление контура при резонансе токов равно бесконечности, а при резонансе напряжений - нулю.

Пример 27.

В схеме на рис.85 задана индуктивность L. Полагая активное сопротивление дросселя нулевым, найти, при каких значениях емкостей ивходное сопротивление схемы для первой гармоники равняется нулю, а для девятой гармоники равно бесконечности.

В соответствии с условиями задания составим систему двух уравнений;

Решим полученную систему уравнений.

(а)

Последнее уравнение получено из уравнения (а) после приведения его к общему знаменателю и приравнивания последнего к нулю.

Пример 28.

Требуется определить эффективные значения тока i и э.д.с. е. Рассчитаем комплексное сопротивление участка bc для первой, третьей и пятой гармоник:

(на третьей гармонике резонанс токов);

Полное сопротивление цепи для соответствующих гармоник:

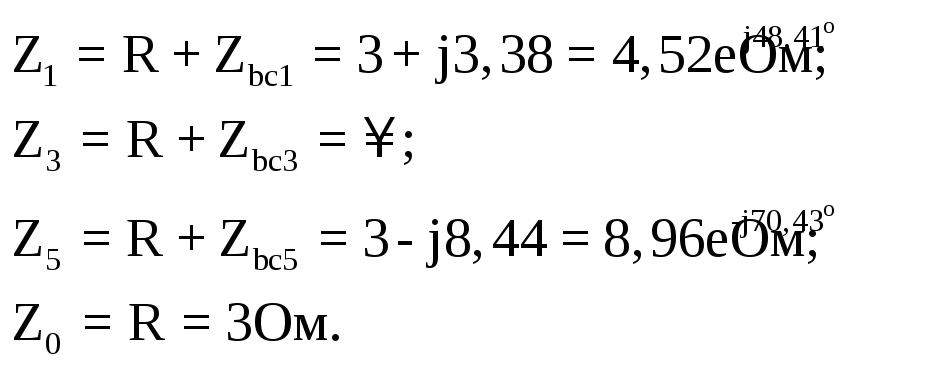
Составляющие тока в неразветвлённой части схемы:

Мгновенное значение тока в неразветвленной части схемы:

Искомые эффективные значения величин:

5.3. Особенности работы трехфазных систем, вызываемые гармониками, кратными трем.

Э.д.с. генератора могут быть искажены, то есть могут быть несинусои-дальными. Будем считать, что каждая из э.д.с. фаз повторяет по форме остальные со сдвигом на 1/3 периода.

При разложении в ряд Фурье k-я гармоника фазы А равна:

Э.д.с. фазы В отстает от э.д.с. фазы А на Т/3, поэтому

Последняя форма записи получена с учетом того, что

Э.д.с. фазы С опережает э.д.с. фазы А на Т/3, следовательно,

Таким образом, третьи (и кратные трем) гармоники во всех трех фазах совпадают по фазе.

Далее обсудим особенности работы трехфазных систем, вызываемые гар­мониками, кратными трем.

1. Если обмотки генератора соединены в треугольник, как показано на рис.87, то по ним будут протекать токи гармоник, кратных трем, даже при отсутствии внешней нагрузки.

Алгебраическая сумма третьих гармоник э.д.с. в треугольнике равна Обозначим сопротивление обмотки каждой фазы для третьей гармони­ки через , тогда ток третьей гармоники в треугольнике равен:

Аналогично для шестой, девятой и т.д.

гармоник.

Действующее значение тока, протека-ющего по замкнутом треугольнику в схеме на рис.87, равно:

.

2. При соединении обмоток генератора в открытый треугольник по схеме на рис.88 при наличии гармоник, кратных трем, на зажимах m и n будет напряжение

.

Показание вольтметра будет равно:

.

3. В линейном напряжении вне зависимости от того, звездой или треугольником соединены обмотки генератора, кратные трем гармоники отсутствуют.

Докажем это свойство для случая холостого хода генератора, т.е. когда внешняя нагрузка отсутствует. Но оно остается в силе и при наличии нагрузки.

Рассмотрим сначала схему соединения треугольником (см. рис.87). Обозначим - потенциал точки А и- потенциал точки В по третьей гармонике, получим

Но , следовательно,

При соединении в звезду (рис.89) линейное напряжение третьей гармоники равно разности соответ-ствующих фазных напряжений. Так как третьи гармоники в фазных напряже-ниях совпадают по фазе, то при составлении этой разности они вычитаются.

В фазном напряжении могут присутствовать все гармоники. Поэтому действующее значение фазного напряжения:

В линейном напряжении (см. рис.89) отсутствуют гармоники, кратные трем, поэтому

Отношение , если есть гармоники, кратные трём.

4.При соединении генератора и равномерной нагрузки в звезду и отсутствии нулевого провода токи, кратных трем гармоник по линейным проводам не протекают. Поэтому между нулевыми точками приемника 0' и генератора 0 будет действовать напряжение:

Действующее значение его

5. Если в схеме звезда-звезда с нулевым проводом при равномерной нагрузке фаз сопротивление нагрузки для третьей гармоники обозначить , а сопротивление нулевого провода для третьей гармоники обозначим, то по нулевому проводу будет протекать ток третьей гармоники, равный:

По каждому из линейных проводов будет протекать ток третьей гармоники

Аналогично находятся токи и от других гармоник, кратных трем.