3.6. Явление резонанса

Пусть пассивный двухполюсник содержит одну или несколько индуктивностей и одну или несколько емкостей (и, конечно, активные сопротивления). Под резонансным режимом работы такого двухполюсника понимают режим, при котором входное сопротивление двухполюсника является чисто активным.

По отношению к внешней цепи двухполюсник в резонансном режиме ведет себя как активное сопротивление, поэтому ток и напряжение на его входе совпадают по фазе. Реактивная мощность двухполюсника при этом равна нулю.

Различают две основные разновидности резонансных режимов: резонанс токов и резонанс напряжений.

Резонанс напряжений возникает в последовательной RLC-цепи, представленной на рис.47, а.

При резонансе ток в цепи должен совпадать по фазе с э.д.с. . Это возможно, если входное сопротивление схемыбудет чисто активным. Условие наступления резонанса в схеме (см. рис.47, а)

Здесь значения противоположных по фазе напряжений на индуктивности и емкости равны, как показано на диаграмме рис.47, б, поэтому резонанс в последовательной цепи получил название резонанса напряжений.

Напряжения на индуктивности и емкости при резонансе могут значительно превышать напряжение на входных зажимах, которое равно напряжению на активном сопротивлении.

Полное сопротивление цепи z при Х=0 минимально: , а ток I максимален.

Резонанса можно достичь, изменяя один из трех параметров: ,L или С. Угловая частота, при которой наступает резонанс, называется угловой резонансной частотой и определяется из условия (43):

(44)

Соответственно резонансная частота

Индуктивное и емкостное сопротивления при резонансе –

Величина называется характеристическим сопротивлением.

Напряжения на реактивных элементах –

Отношение

(45)

называется добротностью резонансного контура. Добротность показывает, во сколько раз напряжение на индуктивном (емкостном) элементе превышает напряжение на входе схемы в резонансном режиме.

Примерный вид зависимости тока от частоты для рассматриваемой схемы (при неизменном значении Е) представлен на рис.48.

Приконденсатор не пропускает ток, прик бес- конечности стремится сопротив-ление индуктивности.

График показывает, что схема обладает избирательными свойствами, которые харак-

теризуются полосой пропускания. Полоса пропускания определяется из условия, что ток на частотахи, соответствующих границе полосы пропускания, уменьшается в раз по сравнению с током при резонансе. Полоса пропускания зависит от Q. Чем больше Q, тем уже полоса пропускания, т.е. лучше избирательность.

Явление резонанса в схеме на рис.49, а с параллельными ветвями, содержащими разнохарактерные реактивные сопротивления, называется резонансом токов.

Ток в ветви с индуктивностью отстаёт от напряжения(см. диаграмму на рис.49, б) и может быть записан как

Ток в ветви с ёмкостью опережает напряжение :

Ток в неразветвлённой части цепи –

По определению резонансного режима, ток должен совпадать по фазе с напряжением. Это будет при условии, что сумма реактивных проводимостей ветвей равна нулю:.

В соответствии с (34)

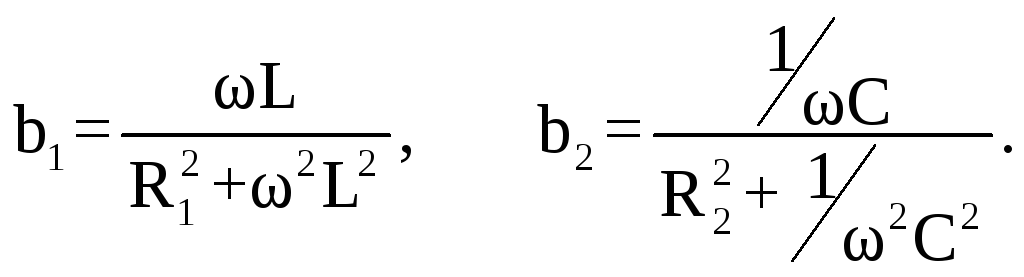
Следовательно, условие наступления режима резонанса токов в схеме на рис.49, а можно записать так:

(46)

Изменением одной из величин в (46) при неизмененных остальных четырех не всегда может быть достигнут резонанс. Резонанс отсутствует, если значение изменяемой величины, вычисленное по (46), получается мнимым или комплексным. Например, решим (46) относительно :

То есть резонанс возможен, если иоба больше или оба меньше

Если в контуре потери малы, что характерно для радиотехники и электросвязи, то можно считать ,и резонансная частота в параллельном контуре будет определяться тем же соотношением, что и в последовательном (см. формулу 44):

Построим зависимость тока от частоты в неразветвленной части схемы (см. рис.49, а) при неизменном приложенном напряжениидля идеального случая

На рис.50 показаны частотные характеристики проводимостей ветвей ии входной проводимости цепиТокпоэтому криваяв соответствующем масштабе и есть резонансная кривая тока.

b22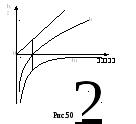

При изменении частоты от 0 до квивалентная проводимостьb<0, т.е. индуктивная, и изменяется от до нуля. Принаступает резонанс токов,иПри возрастании частоты отдовходная проводимостьb>0, т.е. емкостная и изменяется от нуля до .

Пример 17.

Требуется определить величину напряжений на индуктивности и емкости и активную мощность цепи при резонансе.

По формулам (44) и (45) определяем предварительно резонансную частоту и добротность:

Ток в цепи при резонансе

Искомые напряжения и мощность