3. Конструктивный расчет

3.1. Определение расчетных усилий

Статический расчет арок выполняется на отдельные виды загружений: четыре варианта загружений для пологой арки и пять вариантов  для стрельчатой. Ветровую нагрузку при расчете пологой арки обычно не учитывают, т.к. она направлена вверх и по величине обычно меньше снеговой. По усилиям в арке от отдельных нагрузок необходимо составить наиболее неблагоприятные их сочетания, т. е. определить их расчётные значения. Удобнее эту операцию производить в табличной форме (табл. 3).

Вычисления необходимо начать с определения расчётных значений изгибающих моментов M во всех сечениях, кроме конькового и опорного, где изгибающие моменты равны нулю. Это связано с тем, что расчеты на прочность и устойчивость производят на совместное действие изгибающего момента и продольной силы, но определяющей при этом является величина изгибающего момента. Продольная сила в таблице расчетных усилий принимается для тех сочетаний нагрузок, которые дают максимальные значения изгибающего момента.

Расчет на скалывание производится только на действие максимальной поперечной силы, поэтому расчетными для всех сечений являются те сочетания нагрузок, которые дают максимальные значения абсолютной величины поперечной силы.

Схемы загpужения арок даны таким образом, чтобы для левой полуарки определять расчетные сочетания нагрузок, дающие максимальный положительный изгибающий момент, а в правой полуарке максимальный отрицательный изгибающий момент.

В опорных узлах (сечение 1 и 11) и в коньке (сечение 6) изгибающие моменты равны нулю, поэтому в этих сечениях расчетными сочетаниями нагрузок будут те, от которых возникают максимальные продольные (N_max) и максимальные поперечные (Q_max) силы. В ключевом сечении "6" кроме названных усилий необходимо найти продольную силу N₆, соответствующую сочетанию усилий, при котором возникает максимальный изгибающий момент в наиболее нагруженном сечении.

Таблица 3

Усилия от отдельных загружений арки и определение их расчетных значений

№ сечения	Усилия от отдельных нагрузок (кН·м; кН)															Расчетные значения
	Постоянная			Снег 1 вар.			Снег 2 вар.			Снег 3 вар.			Ветровая			M, кН·м	Q, кН	N, кН
	M	Q	N	M	Q	N	M	Q	N	M	Q	N	M	Q	N
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
1	Результаты расчета на ЭВМ															Максимальные значения из вариантов: 2+5+14 2+8+14 2+11+14 для каждого сечения	Максимальные значения из вариантов: 3+6+15 3+9+15 3+12+15 для каждого сечения	Продольная сила в сочетании с +Ммах -Ммах
2
3
4
5
6
7
8
9
10
11

3.2. Определение расчетных усилий в пологих арках с помощью программы «parknew»

В настоящее время большинство расчетов ведется при помощи ЭВМ. Для расчета пологих арок разработана программа «Parknew».

В программе рассматривается 4 варианта нагружения арки:

1 – постоянной распределенной по всему пролету нагрузкой q;

2 – равномерно распределенной снеговой нагрузкой P₁ на всем пролете;

3 – равномерно распределенной снеговой нагрузкой P₁ на поло вине пролета;

4 – треугольной снеговой нагрузкой P₂ на половине пролета.

Загружение пологих арок ветровой нагрузкой в данной программе не рассматривается, так как в большинстве случаев ветровая нагрузка приводит только к снижению общей нагрузки на арку.

Схемы нагружения, расположения точек и основные размеры арки показаны на рис. 3.

Р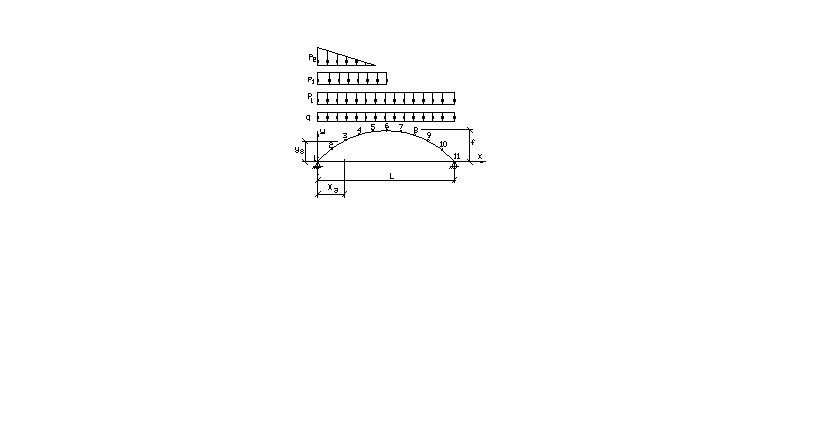ис. 3. Геометрические размеры и схемы нагружения пологой арки

Для расчета пологой арки необходимо предварительно подготовить следующие исходные данные:

- пролет L и стрела подъема f;

- величины постоянной нагрузки и снеговых нагрузоки.

Эти данные вводятся на первом листе таблицы «Excel» (см. рис. 4)

Рис. 4. Ввод исходных данных для расчета пологой арки

Данные сразу же просчитываются. Результаты расчета можно увидеть на втором, третьем и четвертом листах таблицы.

На втором листе рассчитаны координаты точек на оси арки, а также значения и sin и cоsдля каждого рассматриваемого сечения. Далее следуют две таблицы со значениями Q, N, M в арке от равномерно-распределённой нагрузки и равномерно-распределённой снеговой нагрузки. Третий лист содержит результаты расчета значений Q, N, M в арке от снеговой нагрузки на половине пролета и значений Q, N, M в арке от снеговой нагрузки на половине пролета распределенной по закону треугольника. Усилия от отдельных загружений арки и определение их расчетных значений выводятся на листе 4.