3.3 Расчет контура регулирования скорости
Принципиальная электрическая схема регулятора скорости представлена на рисунке 3.4.
Рисунок 3.4 – Принципиальная электрическая схема регулятора скорости
Передаточная функция фильтра на входе регулятора скорости имеет вид:
.
Зададимся значением емкости конденсатора С2=1 мкФ, тогда значения сопротивлений резисторов R9 иR10, причем принимаетсяR9=R10, будут определяться исходя из выражения:
;
R9=R10=24 кОм.
Передаточная функция регулятора скорости имеет вид:
;
Примем величину емкости конденсатора C3 равной 1 мкФ, тогда:
кОм;
;
кОм.
R9+R10=R11=R12=64 кОм.
На рисунке 3.5 представлена электрическая схема задатчика интенсивности скорости.
Рисунок 3.5 – Электрическая схема задатчика интенсивности скорости
Передаточная функция интегратора:
.
Примем С1=10 мкФ, тогда:
кОм.
Принимаем
кОм.
3.4. Расчет контура компенсации эдс
Принципиальная электрическая схема инерционного датчика ЭДС представлена на рисунке 3.6.
Рисунок 3.6 – Принципиальная электрическая схема инерционного датчика ЭДС
Постоянная времени датчика ЭДС определяется из выражения:
,
с
Передаточная функция датчика ЭДС:
.
Примем значение сопротивления R28=27 кОм, тогда значение сопротивленияR29 определится:
R29=
0,523
кОм.
Из стандартного ряда принимаем R29=1 кОм.
Значения сопротивлений R26 иR27 принимаются одинаковыми и равными:
R26=R27=R28/2=27/2=13,5 кОм.
Из стандартного ряда принимаем R26=R27=13 кОм.
Емкость конденсатора С6 определяется:
.
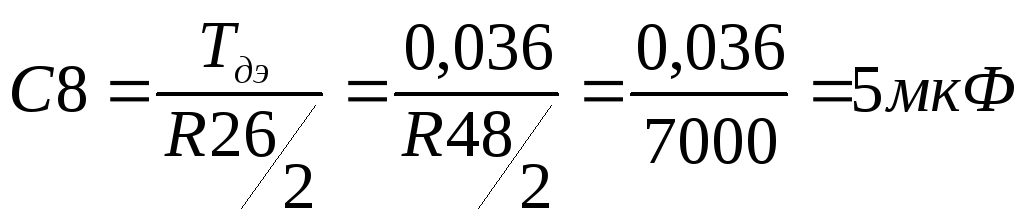Величина сопротивления R30 принимается равнойR28=27 кОм.
Передаточная функция компенсирующего звена имеет вид:
.
где -
,
с – постоянная дифференцирования;
-
- постоянная интегрирования РТ;
-
- эквивалентная электромагнитная
постоянная времени якорной цепи.
Принципиальная электрическая схема компенсирующего звена представлена на рисунке 3.7.
Рисунок 3.7. – Принципиальная схема компенсирующего звена
.
Примем значение емкости конденсатора С1=1 мкФ, тогда значение сопротивления R32 определится::
R32=0,033/C1=0,033/0,000001=33 кОм.
Значение сопротивления R31 определяется:
R31=0,0274/С1=0,0274/0,000001=27,4 кОм.
Из стандартного ряда выбираем R31=R33=27 кОм.
4. Анализ динамических режимов спроектированного электропривода
4.1 Модель САР спроектированного электропривода
Расчет переходных процессов спроектированной системы регулирования производится на ПК с использованием программы Matlab, в системе визуального моделированияSimulink. Структурная схема спроектированной системы регулирования представлена на рисунке 4.1.
Расчет переходных процессов производится на холостом ходу и при номинальной нагрузке.
Рисунок 4.1 – Структурная схема регулирования скорости
4.2. Переходные процессы спроектированного электропривода
4.2.1. Токовый контур
На рисунке 4.2 приведен переходный процесс в токовом контуре при скачкообразном сигнале задания без учета влияния ЭДС двигателя.
4.2
– Переходные процессы в токовом контуре
без учета влияния ЭДС двигателя
На рисунке 4.3 приведен переходный процесс в токовом контуре при скачкообразном сигнале задания с учетом влияния ЭДС двигателя.
.Рисунок 4.3 – Переходный процесс с учетом влияния ЭДС двигателя
На рисунке 4.4 приведен переходный процесс в токовом контуре при скачкообразном сигнале задания с компенсацией ЭДС.
Рисунок 4.4 – Переходный процесс с учетом компенсации влияния ЭДС двигателя
4.2.2 Контур скорости
На рисунках 4.5 и 4.6 приведены переходные процессы в контуре скорости при скачкообразном сигнале задания на холостом ходу и с нагрузкой.
Рисунок 4.5 – Переходный процесс в контуре скорости на холостом ходу
Рисунок 4.6 - Переходный процесс в контуре скорости и тока при набросе нагрузки
4.3. Определение основных параметров качества регулирования
Принцип подчиненного регулирования координат должен обеспечить оптимальные переходные процессы, то есть наименьшее перерегулирование и наибольшее быстродействие.
Если рассматривать контур регулирования тока, то перерегулирование составляет 4,2 %, что удовлетворяет условию модульного оптимума. Применение корректирующего звена, компенсирующего влияние ЭДС двигателя, позволило свести ошибку регулирования тока практически к нулю.
Для электропривода механизма качания кристаллизатора ошибка регулирования скорости не должна превышать 2 %. Это достигается путем применения ПИ регулятора скорости, который сводит ошибку регулирования к нулю. Перерегулирование в контуре скорости также не превышает 4,3 %.
Для обеспечения безыскровой коммутации двигателя применен задатчик интенсивности тока, обеспечивающий темп нарастания тока якоря не превышающий 110 номинальных токов в секунду.