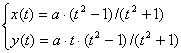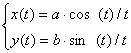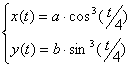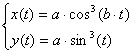Задание по Excel №1

.docx

Скачиваний:

129

Добавлен:

11.02.2015

Размер:

73.21 Кб

Скачать

☆

Задание по Excel №1 Построение двумерного графика

Построить несколько графиков параметрически заданной функции при разных значениях конcтант а, b, . Оси графика – х и y, которые зависят от аргумента t или .

№	Название кривой	Вид графика	Параметрические уравнения	Диапазон аргумента	Кол-во граф.	Значения констант
1	Циклоида				5	a = 1; 1.25; 1.5; 1.75; 2
2	Циклоида				6	a = 2; = 0.4; 0.7; 1.0; 1.3; 1.6; 2.0
3	Трохоида				5	a = -1 b = 0.1; 1; 2; 3; 4
4	Эпитрохоида				6	a = 0; 1; 2; 3; 10; 15 b = 2 = 0.25
5	Гипотрохоида				6	a = 0; 1; 2; 3; 10; 15 b = 2 = 0.25
6	Декартов лист				6	a = 1; 2; 3; 4; 5; 6
7	Циссоида Диоклеса				6	a = 1; 2; 3; 4; 5; 6
8	Строфоида				6	a = 1; 2; 3; 4; 5; 6
9	Конхоида Никомеда				6	a = 1; 2; 3; 4; 5; 6 b = 3
10	Конхоида Никомеда				5	a = 2 b = 1; 10; 30; 50; 90
11	Улитка Паскаля				6	a = 1; 2; 3; 4; 5; 6 b = 3
12	Эпициклоида				6	a = 1 b = 1; 2; 3; 4; 5; 6
13	Эпициклоида				4	(a,b) = (2,7); (3,5); (5,3); (7,2)
14	Эпициклоида				6	a = 3; b = 4 = 0.5; 0.7; 1; 1.5; 2; 3
15	Эпициклоида				6	a = 1; b = 4 = 0.5; 1; 1.5; 2; 4; 6
16	Эпициклоида				6	a = 7; b = 4 = 0.5; 1; 2; 4; 6; 8
17	Гипоциклоида				6	a = 1 b = 1.5; 2.5; 3; 3.5; 4; 5
18	Гипоциклоида				6	a = 1.5; 2; 2.5; 3; 3,5; 4 b = 1
19	Гипоциклоида				6	a = 1; b = 4 = 0.5; 1; 1.5; 2; 3; 4
20	Гипоциклоида				6	a = 5; b = 2 = 0.2; 0.5; 0.7; 1; 1.5; 2
21	Спираль		_<		6	a = 2 b = -2; -1; 1; 2; 3; 4
22	Гиперболи- ческая спираль				5	a = 2 b = 1; 2; 3; 4; 5
23	Гиперболи- ческая спираль				5	a = 3 b = 1; 2; 3; 4; 5
24	Астроида				5	a = 2 b = 1; 2; 3; 4; 5
25	Астроида				5	a = 2 b = 0; 1; 2; 3; 4
26	Астроида				5	a = 2 b = 0.5; 1; 1.5; 3; 3.5
27	Эвольвента				4	a = -2; -1; 1; 2
28	Эвольвента				4	a = -2; -1; 1; 2
29	Эллипс				5	a = 7 b = 1; 4; 7; 10; 13
30	Эллипс				5	a = 3 b = 2 c = 1; 2; 3; 4; 5