
Министерство образования и науки Российской Федерации
ФГБОУ ВПО «Магнитогорский государственный
технический университет им. Г.И. Носова»
Кафедра математических методов в экономике Линейная алгебра
Варианты заданий к контрольной работе № 1 по дисциплине «Линейная алгебра» для студентов заочного факультета направления 080100 «Экономика»
Магнитогорск 2011
Вариант 1
Предприятие выпускает mвидов изделий с использованиемkвидов сырья. Нормы расхода сырья для производства единицы продукции каждого вида даны матрицей Аm×k. Стоимость единицы сырья задана матрицей С. Найти затраты каждого вида сырья при заданном плане выпускаQи суммарные затраты на сырье. Представить результаты с помощью матрицA,C,Q.
А= С=
С= Q=
Q=
Решить матричное уравнение
(5E+A)•X•B = 4•C,
где A= ,
B=
,
B=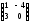 ,
C=
,
C= .
.
Предприятие специализируется по выпуску изделий трех видов: A,B,C; при этом используется сырье трех типов:S1,S2,S3. Нормы расхода каждого вида сырья на единицу изделия каждого вида и объем расхода сырья на 1 день заданы таблицей:
|
Вид сырья |
Расходы сырья на единицу продукции, усл. ед. |
Запасы сырья на один день, усл. ед. | ||
|
A |
B |
C | ||
|
S1 |
2 |
3 |
1 |
1400 |
|
S2 |
4 |
1 |
2 |
1300 |
|
S3 |
1 |
2 |
3 |
1100 |
Найти ежедневный объем выпуска изделий каждого вида.
Получить систему уравнений и решить ее тремя способами: по формулам Крамера, с помощью обратной матрицы и методом Гаусса.
Исследовать совместность, найти общее решение и одно частное решение системы уравнений

2x1+x2-x3-x4+3x5=3
5x1+4x2-4x3-4x4+15x5=9
3x1+2x2-2x3-2x4+7x5=5
Найти общее решение системы линейных уравнений и все базисные решения

x1+x2+2x3-3x4=5
x1+2x2+3x3-5x4=1
Дан параллелограмм ABCD, три вершины которогоA(-1;-2;3),B(-4;1;2),C(5;2;7). Найти четвертую вершину и острый угол параллелограмма.
Найти длину высоты ADв треугольнике с вершинамиA(3;4),B(2;-1),C(1;-7). Написать уравнение перпендикуляра, опущенного из точки С на прямую АВ.
Вариант 2
Предприятие выпускает mвидов изделий с использованиемkвидов сырья. Нормы расхода сырья для производства единицы продукции каждого вида даны матрицей Аm×k. Стоимость единицы сырья задана матрицей С. Найти затраты каждого вида сырья при заданном плане выпускаQи суммарные затраты на сырье. Представить результаты с помощью матрицA,C,Q.
А= С=
С= Q=
Q=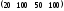
Решить матричное уравнение
(3E+A)•X•(B-4E) =
C, где A=
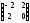 ,
B=
,
B= ,
C=
,
C= .
.
Предприятие специализируется по выпуску изделий трех видов: A,B,C; при этом используется сырье трех типов:S1,S2,S3. Нормы расхода каждого вида сырья на единицу изделия каждого вида и объем расхода сырья на 1 день заданы таблицей:
|
Вид сырья |
Расходы сырья на единицу продукции, усл. ед. |
Запасы сырья на один день, усл. ед. | ||
|
A |
B |
C | ||
|
S1 |
1 |
2 |
4 |
1700 |
|
S2 |
2 |
3 |
5 |
2300 |
|
S3 |
3 |
1 |
2 |
1100 |
Найти ежедневный объем выпуска изделий каждого вида.
Получить систему уравнений и решить ее тремя способами: по формулам Крамера, с помощью обратной матрицы и методом Гаусса.
Исследовать совместность, найти общее решение и одно частное решение системы уравнений

7x1 - 2x2 +2x3 - 2x4 + 3x5 =12
2x1 -x2 +x3 -x4 + 3x5 =3
x1 +x2 -x3 +x4 - 6x5 =3
Найти общее решение системы линейных уравнений и все базисные решения

x1 +x2 –x3 +x4 = 2
-x1 + 2x2 +x3 - 2x4 = -1
Дан параллелограмм ABCD, три вершины которогоA(1;2;3),B(3;-4;-2),C(-4;-3;2). Найти четвертую вершину и острый угол параллелограмма.
Найти длину высоты ADв треугольнике с вершинамиA(3;4),B(2;-1),C(1;-7). Написать уравнение перпендикуляра, опущенного из точки С на прямую АВ.
